备战2023年中考数学细点逐一突破真题训练第15章 圆
试卷更新日期:2023-06-14 类型:二轮复习
一、圆的基本概念及定义
-
1. 下列说法中,正确的是( )A、长度相等的弧是等弧 B、平分弦的直径垂直于弦,并且平分弦所对的两条弧 C、圆的切线垂直于这个圆的半径 D、90°的圆周角所对的弦是圆的直径2. 下列说法中,正确的是( )A、过圆心的线段叫直径 B、长度相等的两条弧是等弧 C、与半径垂直的直线是圆的切线 D、圆既是中心对称图形,又是轴对称图形3. 下列图形中,称为扇形的是( )A、
 B、
B、 C、
C、 D、
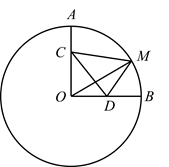
D、 4. 如图,是半圆的直径,四边形和都是正方形,其中点 , , 在上,点 , 在半圆上.若半圆的半径为10,则正方形的面积与正方形的面积之和是( )
4. 如图,是半圆的直径,四边形和都是正方形,其中点 , , 在上,点 , 在半圆上.若半圆的半径为10,则正方形的面积与正方形的面积之和是( ) A、50 B、75 C、100 D、125
A、50 B、75 C、100 D、125二、圆周角定理及其推论
-
5. 如图,点 、 、 在⊙O上, , ,则 的度数是( )
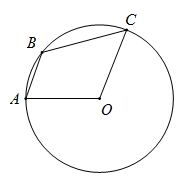 A、110° B、125° C、135° D、165°6. 如图,为的直径,是的弦,、的延长线交于点E,已知 , , 则的度数为( )
A、110° B、125° C、135° D、165°6. 如图,为的直径,是的弦,、的延长线交于点E,已知 , , 则的度数为( ) A、 B、 C、 D、7. 如图,的直径 , 垂足为 , , 连接并延长交于点 , 连接 , 则的度数为( )
A、 B、 C、 D、7. 如图,的直径 , 垂足为 , , 连接并延长交于点 , 连接 , 则的度数为( ) A、 B、 C、 D、8. 如图,AB是⊙O的直径,C,D是⊙O上两点,且CD=CB,CD与AB交于点E,连接OD,若∠AOD=80°,则∠B的度数是( )
A、 B、 C、 D、8. 如图,AB是⊙O的直径,C,D是⊙O上两点,且CD=CB,CD与AB交于点E,连接OD,若∠AOD=80°,则∠B的度数是( )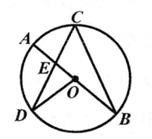 A、20° B、25° C、30° D、35°9. 如图, 是 的直径,点 在 上,若 ,则 °.
A、20° B、25° C、30° D、35°9. 如图, 是 的直径,点 在 上,若 ,则 °.
三、垂径定理及其推论
-
10. 如图所示一张圆形光盘,已知光盘内直径为2cm,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:),那么该光盘的外直径是cm,该光盘的面积是 .
 11. 如图,为的直径,弦交于点 , , , , 则( )
11. 如图,为的直径,弦交于点 , , , , 则( )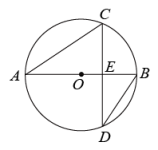 A、 B、 C、1 D、212. 如图1是一款轴对称“磁悬浮地漏”无水时的示意图,它由一个圆弧形密封盖与两个磁体组成(下侧磁体固定不动),连接杆与地面垂直,排水口 , 密封盖最高点E到地面的距离为 , 整个地漏的高度(G为磁体底部中点),密封盖被磁体顶起将排水口密封,所在圆的半径为;当有水时如图2所示,密封盖下移排水,当密封盖下沉至最低处时,点恰好落在中点,若点到的距离为 , 则密封盖下沉的最大距离为.
A、 B、 C、1 D、212. 如图1是一款轴对称“磁悬浮地漏”无水时的示意图,它由一个圆弧形密封盖与两个磁体组成(下侧磁体固定不动),连接杆与地面垂直,排水口 , 密封盖最高点E到地面的距离为 , 整个地漏的高度(G为磁体底部中点),密封盖被磁体顶起将排水口密封,所在圆的半径为;当有水时如图2所示,密封盖下移排水,当密封盖下沉至最低处时,点恰好落在中点,若点到的距离为 , 则密封盖下沉的最大距离为.
四、圆阴影面积
-
13. 如图,为的直径,为上一点,为延长线上一点, , 的半径为5.
 (1)、求证:为的切线;(2)、若 , 求图中阴影部分的面积(结果保留);(3)、若 , 求的长.14. 如图,是等腰直角三角形, , 以BC为直径作交斜边AB于点D,点M是中点,过点M作直线于点E,交AC于点F.
(1)、求证:为的切线;(2)、若 , 求图中阴影部分的面积(结果保留);(3)、若 , 求的长.14. 如图,是等腰直角三角形, , 以BC为直径作交斜边AB于点D,点M是中点,过点M作直线于点E,交AC于点F. (1)、证明:EF是的切线;(2)、若 , 求图中阴影部分面积.15. 如图,是的直径,是的切线,交于点E.
(1)、证明:EF是的切线;(2)、若 , 求图中阴影部分面积.15. 如图,是的直径,是的切线,交于点E. (1)、若D为的中点,求证:是的切线;(2)、若 , , 求的面积.16. 如图,的直径垂直于弦于点F,点P在的延长线上,与相切于点C.
(1)、若D为的中点,求证:是的切线;(2)、若 , , 求的面积.16. 如图,的直径垂直于弦于点F,点P在的延长线上,与相切于点C. (1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.17. 如图,是的内接三角形, , 经过圆心交于点 , 连接 , .
(1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.17. 如图,是的内接三角形, , 经过圆心交于点 , 连接 , . (1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.18. 如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , .
(1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.18. 如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , . (1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.
(1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.五、圆切线相关证明
-
19. 如图,AB是的直径,PA,PC是的两条切线,点A,C为切点,延长PC,AB相交于点D,若BD=1,CD=3,点F为弧AB的中点,连接AC.
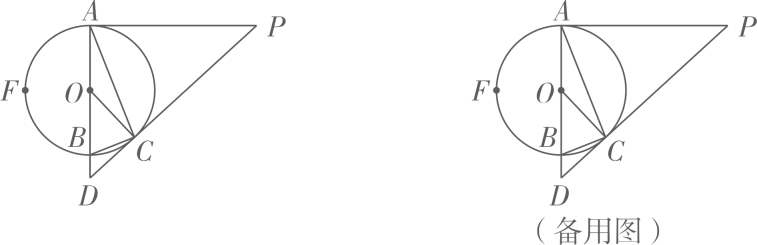 (1)、连接OP交AC于点M,求证:;(2)、设 , 求的值;(3)、若点G与点F关于圆心O对称,连接CG,求CG的长.20. 如图,的半径是 , AB是的直径,半径于点O,点E是半径上一点,交于点D,且.
(1)、连接OP交AC于点M,求证:;(2)、设 , 求的值;(3)、若点G与点F关于圆心O对称,连接CG,求CG的长.20. 如图,的半径是 , AB是的直径,半径于点O,点E是半径上一点,交于点D,且. (1)、求证:是的切线;(2)、若 , 求:和的长.
(1)、求证:是的切线;(2)、若 , 求:和的长.六、圆与锐角三角函数
-
21. 如图,AC是⊙O的弦,AC=4,点B是⊙O上的一个动点,且∠ABC=45°,若点M,N分别是AC,BC的中点,则MN的最大值为( )
 A、 B、4 C、6 D、22. 如图,中, , , , 以为直径作 , 交于点F,连接并延长,分别交于D、E两点,连接、 .
A、 B、4 C、6 D、22. 如图,中, , , , 以为直径作 , 交于点F,连接并延长,分别交于D、E两点,连接、 . (1)、求证:是的切线;(2)、求证:;(3)、求的正切值.23. 如图,为的直径,C,D为上两点,连接 , , , , 线段与相交于点E,过点D作 , 交的延长线于点F.
(1)、求证:是的切线;(2)、求证:;(3)、求的正切值.23. 如图,为的直径,C,D为上两点,连接 , , , , 线段与相交于点E,过点D作 , 交的延长线于点F. (1)、求证:是的切线;(2)、若 , , , 求的半径.24. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)、求证:是的切线;(2)、若 , , , 求的半径.24. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.七、网格作图
-
25. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
 (1)、如图1,△ABC的外接圆的圆心是点O,D是弧BC的中点,画一条弦AE把△ABC分成面积相等的两部分;(2)、如图2,△ABC是⊙O的内接三角形,且AB=AC,过点B画弦BD∥AO;(3)、如图3,△ABC是⊙O的内接三角形,弦AD∥BC,画∠BAC的平分线交BC于点E.26. 如图,由小正方形构成的网格中,每个小正方形的顶点叫做格点,经过A,B,C三个格点,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线,结果用实线).
(1)、如图1,△ABC的外接圆的圆心是点O,D是弧BC的中点,画一条弦AE把△ABC分成面积相等的两部分;(2)、如图2,△ABC是⊙O的内接三角形,且AB=AC,过点B画弦BD∥AO;(3)、如图3,△ABC是⊙O的内接三角形,弦AD∥BC,画∠BAC的平分线交BC于点E.26. 如图,由小正方形构成的网格中,每个小正方形的顶点叫做格点,经过A,B,C三个格点,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线,结果用实线). (1)、在图1中标出圆心O,并在圆上找一点E,使平分弧;(2)、在图2中的圆上画一点M,使平分.(3)、如图3,的顶点A,B均在格点上,顶点C在网格线上, , P是如图所示的的外接圆上的动点,当时,请用无刻度的直尺,在圆上画出点P.27. 如图是由小正方形组成的网格,每个小正方形的顶点叫作格点已知的圆心在格点上,圆上 , 两点均在格线上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、在图1中标出圆心O,并在圆上找一点E,使平分弧;(2)、在图2中的圆上画一点M,使平分.(3)、如图3,的顶点A,B均在格点上,顶点C在网格线上, , P是如图所示的的外接圆上的动点,当时,请用无刻度的直尺,在圆上画出点P.27. 如图是由小正方形组成的网格,每个小正方形的顶点叫作格点已知的圆心在格点上,圆上 , 两点均在格线上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. (1)、在图1中,点在圆上,请在直径下方的圆上画出点 , 使;并在网格中找点 , 使为等腰直角三角形,且 .(2)、在图2中,为格点,在直径下方的圆上画出点 , 使得;并在线段上画出点 , 使得 .
(1)、在图1中,点在圆上,请在直径下方的圆上画出点 , 使;并在网格中找点 , 使为等腰直角三角形,且 .(2)、在图2中,为格点,在直径下方的圆上画出点 , 使得;并在线段上画出点 , 使得 .八、圆中有关线段的计算
-
28. 如图,在中,是上一点, , 平分交于点 , 连结 , .
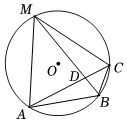 (1)、求证:是正三角形;(2)、若 , 求半径的长.29. 如图,是的直径,C是弧的中点,于点E,交于点F.
(1)、求证:是正三角形;(2)、若 , 求半径的长.29. 如图,是的直径,C是弧的中点,于点E,交于点F. (1)、求证:;(2)、若 , , 求的半径及的长.30. 如图, 是 的直径, 是圆上的一点, 为 的中点,过点 作 的切线与 的延长线交于点 ,与 的延长线交于点 ,弦 、 交于点 .
(1)、求证:;(2)、若 , , 求的半径及的长.30. 如图, 是 的直径, 是圆上的一点, 为 的中点,过点 作 的切线与 的延长线交于点 ,与 的延长线交于点 ,弦 、 交于点 . (1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.31. 如图,AB是的直径,AE是的切线,点C为直线AE上一点,连接OC交于点D,连接BD并延长交线段AC于点E.
(1)、求证: ;(2)、求证: ;(3)、若 , ,求 的长.31. 如图,AB是的直径,AE是的切线,点C为直线AE上一点,连接OC交于点D,连接BD并延长交线段AC于点E. (1)、求证:;(2)、若 , , 求的半径.32. 如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H.
(1)、求证:;(2)、若 , , 求的半径.32. 如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H. (1)、求证:CD是⊙O的切线;(2)、求sin∠FHG的值;(3)、若GH= , HB=2,求⊙O的直径.33. 如图,在中, , , .用直尺和圆规按下列步骤作图:
(1)、求证:CD是⊙O的切线;(2)、求sin∠FHG的值;(3)、若GH= , HB=2,求⊙O的直径.33. 如图,在中, , , .用直尺和圆规按下列步骤作图:①以点B为圆心,适当的长为半径画弧,分别交边BC,AB于点D,E;
②分别以点D,E为圆心,大于的长为半径画弧,两弧交于点P;
③作射线BP,交边AC于点O;
④以点O为圆心,OC的长为半径画 , 交射线BP于点F,G(点G在线段OB上),连接CF,CG.
 (1)、求证:AB是的切线;(2)、求的半径长;(3)、求的值.34. 如图,内接于半圆O,已知是半圆O的直径. , 平分 , 分别交半圆O和于点 , 过点D作 , 垂足为点H,交于点F.
(1)、求证:AB是的切线;(2)、求的半径长;(3)、求的值.34. 如图,内接于半圆O,已知是半圆O的直径. , 平分 , 分别交半圆O和于点 , 过点D作 , 垂足为点H,交于点F. (1)、求证:;(2)、连接交于点G,若 , 求的长.35. 如图,是的直径,点C是上一点,与过点C的切线垂直,垂足为点D,切线与的延长线相交于点P,弦平分 , 交于点F,连接 ,
(1)、求证:;(2)、连接交于点G,若 , 求的长.35. 如图,是的直径,点C是上一点,与过点C的切线垂直,垂足为点D,切线与的延长线相交于点P,弦平分 , 交于点F,连接 , (1)、若 , , 则 弧的长为.(2)、若 , , 则的长为.
(1)、若 , , 则 弧的长为.(2)、若 , , 则的长为.九、阿氏圆、隐含圆问题
-
36. 如图,在⊙O中,点A、点B在⊙O上,∠AOB=90°,OA=6,点C在OA上,且OC=2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为.