浙江省舟山市2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 下列各数中,为无理数的是( )A、 B、0 C、 D、3.52. 下列计算中,正确的是( )A、 B、 C、 D、3. 若 , 下列各式中一定成立的是( )A、 B、 C、 D、4. 在平面直角坐标系中,已知点 , 以原点O为位似中心,相似比为 , 把缩小,则点A的对应点的坐标是( )A、 B、 C、或 D、或5. 某天气预报软件显示“舟山市定海区明天的降水概率为85%”,对这条信息的下列说法中,正确的是( )A、定海区明天下雨的可能性较大 B、定海区明天下雨的可能性较小 C、定海区明天将有85%的时间下雨 D、定海区明天将有85%的地区下雨6. 如图,在的两边上分别截取、 , 使;分别以点A、B为圆心,长为半径作弧,两弧交于点C;连接、、、 . 若 , 四边形的面积为 . 则的长为( )
 A、 B、 C、 D、7. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )
A、 B、 C、 D、7. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( ) A、S矩形ABMN=S矩形MNDC B、S矩形EBMF=S矩形AEFN C、S矩形AEFN=S矩形MNDC D、S矩形EBMF=S矩形NFGD8. 如图,一次函数的图象与反比例函数的图象交于点 , , 当时,的取值范围是( )
A、S矩形ABMN=S矩形MNDC B、S矩形EBMF=S矩形AEFN C、S矩形AEFN=S矩形MNDC D、S矩形EBMF=S矩形NFGD8. 如图,一次函数的图象与反比例函数的图象交于点 , , 当时,的取值范围是( ) A、或 B、或 C、或 D、或9. 如图,将矩形沿直线折叠,使点B落在点E处,连接 , 若 , 则的值为( )
A、或 B、或 C、或 D、或9. 如图,将矩形沿直线折叠,使点B落在点E处,连接 , 若 , 则的值为( ) A、 B、 C、 D、10. 已知函数(a为常数),当时,y随x增大而增大.是该函数图象上的两点,对任意的和 , 总满足 , 则实数a的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知函数(a为常数),当时,y随x增大而增大.是该函数图象上的两点,对任意的和 , 总满足 , 则实数a的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 在一次科学课上,小明同学设计了如下电路图,随机闭合两个开关,能使其中1个灯泡发亮的概率为 .
 13. 如图,A、B、C为上三点,若 , 则度数为°.
13. 如图,A、B、C为上三点,若 , 则度数为°.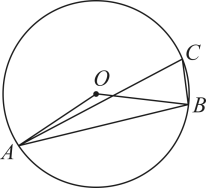 14. 如图,中, , 点在上,且 , 点在上,连接 . 若 , 则 .
14. 如图,中, , 点在上,且 , 点在上,连接 . 若 , 则 . 15. 把量角器和含角的三角板按如图1方式摆放,将其抽象为图2:若与相切于点E, , . 则阴影部分的面积为 .
15. 把量角器和含角的三角板按如图1方式摆放,将其抽象为图2:若与相切于点E, , . 则阴影部分的面积为 . 16. 如图,是等边三角形,点分别为边上的动点,运动过程中始终保持 . 连结 , 在右侧作等边三角形 , 并连结 .
16. 如图,是等边三角形,点分别为边上的动点,运动过程中始终保持 . 连结 , 在右侧作等边三角形 , 并连结 . (1)、当时,若 , 则 .(2)、在点从点运动到点的过程中,若的最小值为 , 则边长是 .
(1)、当时,若 , 则 .(2)、在点从点运动到点的过程中,若的最小值为 , 则边长是 .三、解答题
-
17.(1)、计算:(2)、化简:18. 观察: , , , .(1)、猜想:当时, , , (“>”“=”“<”填空)(2)、探究:当时,与(其中n为正整数)的大小关系,并说明理由.19. 德国心理学家艾宾浩斯研究发现,遗忘在新事物学习之后立即开始,而且遗忘的进程并不是均匀的.如果把学习后的时间记为x(时),记忆留存率记为y(%),则根据实验数据可绘制出曲线(如图所示),即著名的“艾宾浩斯遗忘曲线”.该曲线对人类记忆认知研究产生了重大影响.
 (1)、y是关于x的函数吗?为什么?(2)、请说明点D的实际意义.(3)、根据图中信息,对新事物学习提出一条合理的建议.20. 为了解我国铁路旅客发送量和货运总发送量,小明同学在中华人民共和国交通运输部网上查询到2022年7月到2023年2月,全国铁路旅客发送量和货运总发送量的数据,并绘制了如下的折线统计图.
(1)、y是关于x的函数吗?为什么?(2)、请说明点D的实际意义.(3)、根据图中信息,对新事物学习提出一条合理的建议.20. 为了解我国铁路旅客发送量和货运总发送量,小明同学在中华人民共和国交通运输部网上查询到2022年7月到2023年2月,全国铁路旅客发送量和货运总发送量的数据,并绘制了如下的折线统计图.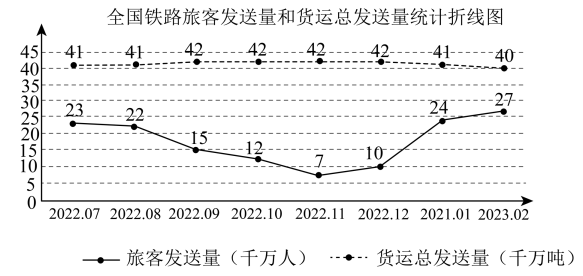
根据图表信息,回答下列问题:
(1)、2022年12月至2023年1月的旅客发送量的增长率为 .(2)、估计从2023年3月到2023年12月,10个月的货运总发送量,小明选用了平均数来分析,小军选用众数来分析.①请从小明和小军两个选用的统计量分别估计货运总发送量.
②分别说明两种的合理性,请通过计算说明.
(3)、请结合折线统计图,对2022年7月至2023年2月我国旅客发送量和货运总发送量,并结合实际情况你还可以得到什么信息?21. 如图,在中, , 过点D作交的延长线于点E,连接交于点F. (1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长.22. “五一”节期间,洞庭湖旅游度假区特色文旅活动精彩上演,吸引众多市民打卡游玩,许多露营爱好者在大烟囱草坪露营,为遮阳和防雨游客们搭建了一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合, , .
(1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长.22. “五一”节期间,洞庭湖旅游度假区特色文旅活动精彩上演,吸引众多市民打卡游玩,许多露营爱好者在大烟囱草坪露营,为遮阳和防雨游客们搭建了一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合, , . (1)、天晴时打开“天幕”,若 , 求遮阳宽度(结果精确到0.1m);(2)、下雨时收拢“天幕”, 从减少到 , 求点下降的高度(结果精确到0.1m).
(1)、天晴时打开“天幕”,若 , 求遮阳宽度(结果精确到0.1m);(2)、下雨时收拢“天幕”, 从减少到 , 求点下降的高度(结果精确到0.1m).(参考数据: , , , )
23. 在平面直角坐标系中,抛物线(b,c是常数)经过点 , 点B . 点P在此抛物线上,其横坐标为m.(1)、求此抛物线的解析式.(2)、若时, , 则d的取值范围是 .(3)、点P和点A之间(包括端点)的函数图象称为图象G,当图象G的最大值和最小值差是5时,求m的值.24. 如图1,在中,直径于点F,点E为上一点,点C为弧的中点,连接 , 交于点G. (1)、求证:;(2)、如图2,过点C作的切线交BA的延长线于点Q,若 , , 求的长度;(3)、在(2)的基础上,点P为上任一点,连接 , 的比值是否发生改变?若不变,求出比值;若变化,说明变化规律.
(1)、求证:;(2)、如图2,过点C作的切线交BA的延长线于点Q,若 , , 求的长度;(3)、在(2)的基础上,点P为上任一点,连接 , 的比值是否发生改变?若不变,求出比值;若变化,说明变化规律.