浙江省温州市永嘉县2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
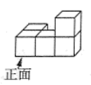
1. 2023的倒数是( )A、2023 B、 C、-2023 D、2. 如图所示的几何体是由五个小正方体搭建而成的,则左视图是( )
 A、
A、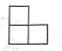 B、
B、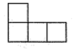 C、
C、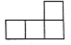 D、
D、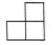 3. 为了解某市九年级男生的身高情况,随机抽取了该市100名九年级男生,他们的身高 统计如下:
3. 为了解某市九年级男生的身高情况,随机抽取了该市100名九年级男生,他们的身高 统计如下:组别
人数
15
42
38
5
根据以上结果,全市约有 万男生,估计全市男生的身高不高于 的人数是( )
A、 B、 C、 D、4. 一个袋子中装有3个黑球和4个白球,这些球除颜色外其他都相同,随机从袋子中摸出一个球,摸到白球的概率为( )A、 B、 C、 D、5. 买一个足球需元,买一个篮球需元,则买5个足球和4个篮球共需( )A、元 B、元 C、元 D、元6. 若关于x的一元二次方程 , 有两个相等的实数根,则正数b的值是( )A、8 B、-8 C、4 D、-47. 如图,点 , , , 均在以点 为圆心的圆 上,连接 , 及顺次连接 , , , 得到四边形 ,若 , ,则 的度数为( ) A、20° B、25° C、30° D、35°8. 如图,正方形的边长为 , 点P,Q同时从点A出发,速度均为 , 若点P沿向点C运动,点Q沿向点C运动,则的面积与运动时间之间函数关系的大致图象是( )
A、20° B、25° C、30° D、35°8. 如图,正方形的边长为 , 点P,Q同时从点A出发,速度均为 , 若点P沿向点C运动,点Q沿向点C运动,则的面积与运动时间之间函数关系的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
9. 已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( ) A、有最大值 1.5,有最小值﹣2.5 B、有最大值 2,有最小值 1.5 C、有最大值 2,有最小值﹣2
A、有最大值 1.5,有最小值﹣2.5 B、有最大值 2,有最小值 1.5 C、有最大值 2,有最小值﹣2 5
D、有最大值 2,无最小值
10. 如图,在Rt△ABC中,∠BAC=90° , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连结KN交AG于点M,若S1-S2=2,AC=4,则AB的长为 ( )
5
D、有最大值 2,无最小值
10. 如图,在Rt△ABC中,∠BAC=90° , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连结KN交AG于点M,若S1-S2=2,AC=4,则AB的长为 ( )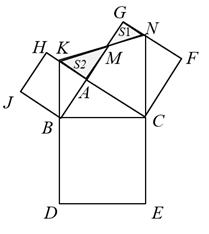 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 因式分解 .12. 某校5个小组在一次植树活动中植树株数的统计图如图所示,则平均每组植树株.
 13. 计算: .14. 若扇形的圆心角为 , 半径为 , 则它的弧长是 .15. 如图是一张矩形纸片 , 点为中点,点在上,把该纸片沿折叠,点的对应点分别为与相交于点 , 的延长线过点 . 若 , 则的值为 .
13. 计算: .14. 若扇形的圆心角为 , 半径为 , 则它的弧长是 .15. 如图是一张矩形纸片 , 点为中点,点在上,把该纸片沿折叠,点的对应点分别为与相交于点 , 的延长线过点 . 若 , 则的值为 . 16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段 , 过作 , 然后依次作垂线段 , 直到接近点,作于点 . 每条线段可测量,长度如图所示.分别在 , 上任选点 , 作 , , 使得 , 此时点共线.挖隧道时始终能看见处的标志即可.
16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段 , 过作 , 然后依次作垂线段 , 直到接近点,作于点 . 每条线段可测量,长度如图所示.分别在 , 上任选点 , 作 , , 使得 , 此时点共线.挖隧道时始终能看见处的标志即可. (1)、 km.(2)、 = .
(1)、 km.(2)、 = .三、解答题
-
17.(1)、计算:(2)、解不等式: , 并在数轴上将解集表示出来.
 18. 图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,分别按要求在网格内画出格点图形顶点均在格点上.
18. 图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,分别按要求在网格内画出格点图形顶点均在格点上. (1)、在图1中以为对角线画一个四边形 , 使得;(2)、在图2中以点为顶点画一个菱形 , 使得.19. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康,某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭进行一次简单随机抽样调查.(1)、下列选取样本的方法最合理的一种是 . (只需填上正确答案的序号)
(1)、在图1中以为对角线画一个四边形 , 使得;(2)、在图2中以点为顶点画一个菱形 , 使得.19. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康,某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭进行一次简单随机抽样调查.(1)、下列选取样本的方法最合理的一种是 . (只需填上正确答案的序号)①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
(2)、本次抽样调查发现,接受调查的家庭都有过期药品.现将有关数据呈现如图: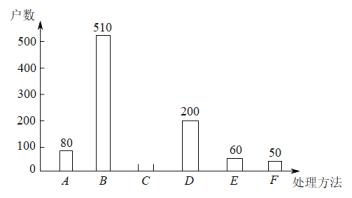
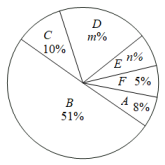

①m=▲ , n=▲ ;
②补全条形统计图;
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
20. 如图,在中, , , 平分交于点D,过点A作 , 交的延长线于点E.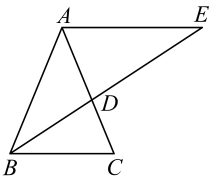 (1)、求的度数.(2)、求证:是等腰三角形.21. 如图所示,在中,设边的长为x,边上的高线长为y,已知的面积等于24.
(1)、求的度数.(2)、求证:是等腰三角形.21. 如图所示,在中,设边的长为x,边上的高线长为y,已知的面积等于24. (1)、求y关于x的函数表达式及自变量x的取值范围.(2)、当时,求y的取值范围.22. 如图,在矩形ABCD中,点E在BC边上,且DE=AD,过点A作AF∥DE交CB的延长线于点F.
(1)、求y关于x的函数表达式及自变量x的取值范围.(2)、当时,求y的取值范围.22. 如图,在矩形ABCD中,点E在BC边上,且DE=AD,过点A作AF∥DE交CB的延长线于点F. (1)、求证:四边形AFED是菱形;(2)、若AB=1,CF=2.
(1)、求证:四边形AFED是菱形;(2)、若AB=1,CF=2.①求AD的长;
②AE、FD交于点O,连接OC,求OC的长.
23. 根据以下素材,探索完成任务.如何设计跳长绳方案
素材1
图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人.图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
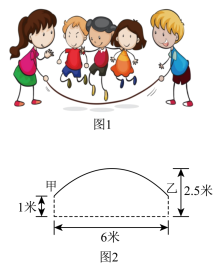
素材2
某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.68米.跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米.
问题解决
任务1
确定长绳形状
在图2中建立合适的直角坐标系,并求出抛物线的函数表达式.
任务2
探究站队方式
当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3
拟定位置方案
为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位.请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
24. 如图1,在中, , , . 点D为AB的中点,过点D作射线交于点E,点M为射线上一动点,过点M作于点N,点P为边上一点,连结 , 且满足 , 设 , .

 (1)、求线段的长.(2)、求y关于x的函数表达式.(3)、如图2,连结 .
(1)、求线段的长.(2)、求y关于x的函数表达式.(3)、如图2,连结 .①当为等腰三角形时,求x的值.
②以点M为旋转中心,将线段按顺时针方向旋转90°得线段 , 当点落在边上时,求的值.