浙江省金华市2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 在实数-2, , , 0.1122中,无理数的是( )A、-2 B、 C、 D、0.11222. 计算的结果是( )A、 B、 C、6 D、3. 下列四个立体图形中,主视图为圆的是( )A、
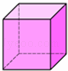 B、
B、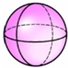 C、
C、 D、
D、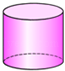 4. 不等式组的解集在数轴上表示正确的是( )A、
4. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 在中,点 , , , 都在圆周上, , , 则的度数为( )
5. 在中,点 , , , 都在圆周上, , , 则的度数为( )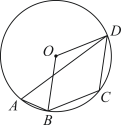 A、 B、 C、 D、6. 下列关于过直线l外一点P作直线l的平行线的尺规作图错误的是( )A、
A、 B、 C、 D、6. 下列关于过直线l外一点P作直线l的平行线的尺规作图错误的是( )A、 B、
B、 C、
C、 D、
D、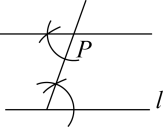 7. 点在反比例函数的图像上,当时,y的取值范围是( )A、 B、 C、 D、8. 如图,在四边形 中, 是 边的中点,连接 并延长,交 的延长线于点 , .添加一个条件使四边形 是平行四边形,你认为下面四个条件中可选择的是( )
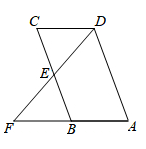
7. 点在反比例函数的图像上,当时,y的取值范围是( )A、 B、 C、 D、8. 如图,在四边形 中, 是 边的中点,连接 并延长,交 的延长线于点 , .添加一个条件使四边形 是平行四边形,你认为下面四个条件中可选择的是( )
 A、 B、 C、 D、9. 如图,两个高度相等且底面直径之比为的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点的距离是( ).
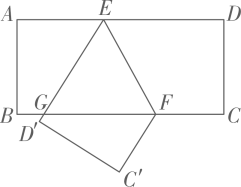
A、 B、 C、 D、9. 如图,两个高度相等且底面直径之比为的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点的距离是( ). A、 B、 C、 D、10. 如图,直线与坐标轴相交于点A,B.分别以 , 为直角边,以B为直角顶点,在的外部作等腰 , 等腰 , 与y轴相交于点E,则的值为( )
A、 B、 C、 D、10. 如图,直线与坐标轴相交于点A,B.分别以 , 为直角边,以B为直角顶点,在的外部作等腰 , 等腰 , 与y轴相交于点E,则的值为( ) A、4 B、7 C、 D、不能确定
A、4 B、7 C、 D、不能确定二、填空题
-
11. 函数y= 中,自变量x的取值范围是 .12. 若 是同类项,则 .13. 在一个不透明的袋中,只有白、红颜色的球,这些球除颜色外完全相同,已知从袋中随机摸出一个红球的概率为 , 则随机摸出一个白球的概率是 .14. 已知等腰的周长为10,若设腰长为x,则x的取值范围是 .15. 如图,将矩形纸片沿折叠,点落在 , , 且 , , 三点在同一直线上,与交于点 , 记的周长为 , 若 , 则的值为 .
 16. 某品牌水果冻的高为3cm,底面圆的直径为4cm,两个水果冻倒装在一个长方体盒子内,如图为横断示意图,水果冻的截面可以近似地看成两条抛物线.以左侧抛物线的顶点O为原点,建立如图所示的直角坐标系.
16. 某品牌水果冻的高为3cm,底面圆的直径为4cm,两个水果冻倒装在一个长方体盒子内,如图为横断示意图,水果冻的截面可以近似地看成两条抛物线.以左侧抛物线的顶点O为原点,建立如图所示的直角坐标系.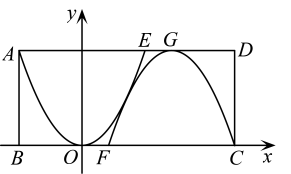 (1)、以O为顶点的抛物线的函数表达式是 .(2)、制作该长方体盒子所需纸张面积最小值是cm2 . (不计重叠部分)
(1)、以O为顶点的抛物线的函数表达式是 .(2)、制作该长方体盒子所需纸张面积最小值是cm2 . (不计重叠部分)三、解答题
-
17. 计算 .18. 先化简,再求值: , 其中 .19. 小明对本校八年级530名学生的体育达标情况进行调查,按A,B,C三等成绩进行统计并制作出如图所示的统计图,其中,(1)班有50人,A等成绩为40以上,B等成绩为(不含40),C等为不达标,成绩为(不含30).根据图中信息解答下面问题:
 (1)、若除1班外,其余班级学生体育考试成绩在B等的有120人,请补全扇形统计图.(2)、若要求全年级学生的体育达标率不低于90%,在本次调查中,该年级全体学生的体育达标率是否符合要求?如果不符合要求,还需要增加几个同学的成绩达标?20. 如图,垂直于地平线的旗杆上系一旗帜,在距旗杆底部点6米的D处有一坡比为的斜坡 . 旗帜在点C时,其影子落在斜坡端点D,测得旗高;继续拉动旗帜到杆顶A时,其影子落在斜坡上的E点,测得 .
(1)、若除1班外,其余班级学生体育考试成绩在B等的有120人,请补全扇形统计图.(2)、若要求全年级学生的体育达标率不低于90%,在本次调查中,该年级全体学生的体育达标率是否符合要求?如果不符合要求,还需要增加几个同学的成绩达标?20. 如图,垂直于地平线的旗杆上系一旗帜,在距旗杆底部点6米的D处有一坡比为的斜坡 . 旗帜在点C时,其影子落在斜坡端点D,测得旗高;继续拉动旗帜到杆顶A时,其影子落在斜坡上的E点,测得 . (1)、求坡角的度数(2)、求旗杆的高度.21. 如图所示,取某一位置的水平线为轴,建立了平面坐标系后,小山坡可以近似看成抛物线 . 小明在离点的楼顶抛出一球,其运动轨迹为抛物线 , 落在山坡的点处,测得点离轴的距离为 .
(1)、求坡角的度数(2)、求旗杆的高度.21. 如图所示,取某一位置的水平线为轴,建立了平面坐标系后,小山坡可以近似看成抛物线 . 小明在离点的楼顶抛出一球,其运动轨迹为抛物线 , 落在山坡的点处,测得点离轴的距离为 . (1)、求点的坐标.(2)、求小球飞行过程中,离山坡的最大高度.22. 如图,为的直径,点在上,过点作的切线交的延长线于点 , 已知
(1)、求点的坐标.(2)、求小球飞行过程中,离山坡的最大高度.22. 如图,为的直径,点在上,过点作的切线交的延长线于点 , 已知 (1)、求的度数;(2)、若弦 , 垂足为 , 且 , 求图中阴影部分的面积.
(1)、求的度数;(2)、若弦 , 垂足为 , 且 , 求图中阴影部分的面积.

