陕西省宝鸡市凤翔区2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 如图,这是一个由6个相同的正方体组成的立体图形,它的左视图是( )
 A、
A、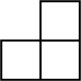 B、
B、 C、
C、 D、
D、 3. 如图, , 若 , , 则的度数为( )
3. 如图, , 若 , , 则的度数为( )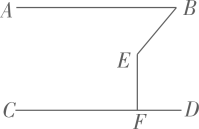 A、 B、 C、 D、4. 有理数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
A、 B、 C、 D、4. 有理数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )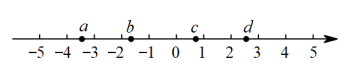 A、 B、 C、 D、5. 如图,点是菱形边的中点,点在边上,连接 , 过点作交对角线于点 , 交于点 . 若 , , 则线段的长为( )
A、 B、 C、 D、5. 如图,点是菱形边的中点,点在边上,连接 , 过点作交对角线于点 , 交于点 . 若 , , 则线段的长为( )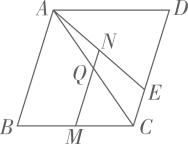 A、4 B、5 C、6 D、76. 一次函数的图象不经过第三象限,则( )A、 , B、 , C、 , D、 ,7. 如图, , 是的两条直径,点是劣弧的中点,连接 , . 若 , 则的度数为( )
A、4 B、5 C、6 D、76. 一次函数的图象不经过第三象限,则( )A、 , B、 , C、 , D、 ,7. 如图, , 是的两条直径,点是劣弧的中点,连接 , . 若 , 则的度数为( )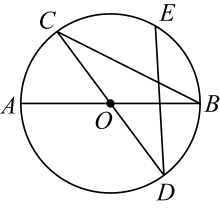 A、 B、 C、 D、8. 已知抛物线经过点 , 将点A先向右平移3个单位,再向下平移b个单位恰好落在抛物线的最低点处,则b的值为( )A、3 B、4 C、5 D、9
A、 B、 C、 D、8. 已知抛物线经过点 , 将点A先向右平移3个单位,再向下平移b个单位恰好落在抛物线的最低点处,则b的值为( )A、3 B、4 C、5 D、9二、填空题
-
9. 因式分解= .10. 七巧板是中国民间流传的一种传统智力玩具,它是由等腰直角三角形,正方形和平行四边形组成的.如图,有一块边长为的正方形厚纸板 , 做成如图①所示的一套七巧板(点为正方形纸板对角线的交点,点、分别为、的中点, , ),将图①示七巧板拼成如图②所示的“鱼形”,则“鱼尾”的长为 .
 11. 如图,为等边三角形, , , 若将沿轴向左平移2个单位后,得到的 , 则点的坐标为 .
11. 如图,为等边三角形, , , 若将沿轴向左平移2个单位后,得到的 , 则点的坐标为 . 12. 在平面直角坐标系中,点 , 在反比例函数的图象上,若 , 则k0(填“>”或“<”).13. 如图,正方形边长为2,点是以为直径的半圆上的一个动点,点是边上的一个动点,点是的中点,则的最小值为 .
12. 在平面直角坐标系中,点 , 在反比例函数的图象上,若 , 则k0(填“>”或“<”).13. 如图,正方形边长为2,点是以为直径的半圆上的一个动点,点是边上的一个动点,点是的中点,则的最小值为 .
三、解答题
-
14. 计算: .15. 解不等式组:16. 先化简,再求值: , 其中 .17. 如图,在中, , 是的边上的中线,请用尺规作图法在边上求作一点 , 使得 . (不写作法,保留作图痕迹)
 18. 如图,点 , , , 在同一条直线上, , , . 求证: .
18. 如图,点 , , , 在同一条直线上, , , . 求证: .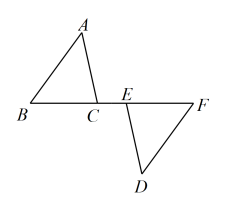 19. 如图,小明用一张正方形纸片剪出两个宽都是的长条,如果其中一个长条的面积是另一个长条的1.2倍,求原来正方形纸片的边长.
19. 如图,小明用一张正方形纸片剪出两个宽都是的长条,如果其中一个长条的面积是另一个长条的1.2倍,求原来正方形纸片的边长. 20. 甲、乙两人用如图所示的两个转盘做游戏,转盘被等分为三份,分别标有数字1,2,-3;转盘也被等分成三份,分别标有数字-1,-2,3.甲乙两人同时转动转盘,当转盘停止转动时,记下两个转盘指针所指的数字之和.若指针所指数字之和为正数,则甲胜;指针所指数字之和为负数,则乙胜.
20. 甲、乙两人用如图所示的两个转盘做游戏,转盘被等分为三份,分别标有数字1,2,-3;转盘也被等分成三份,分别标有数字-1,-2,3.甲乙两人同时转动转盘,当转盘停止转动时,记下两个转盘指针所指的数字之和.若指针所指数字之和为正数,则甲胜;指针所指数字之和为负数,则乙胜.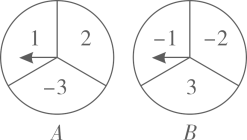 (1)、转动转盘一次,指针所指数字为负数的概率是;(2)、请用列表或画树状图的方法说明这个游戏对甲乙两人是否公平.21. 如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东53°方向,距离B地516千米,C地位于A地南偏东45°方向.现打算打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(结果精确到1千米)(参考数据:sin53°= ,cos53°= ,tan53°= )
(1)、转动转盘一次,指针所指数字为负数的概率是;(2)、请用列表或画树状图的方法说明这个游戏对甲乙两人是否公平.21. 如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东53°方向,距离B地516千米,C地位于A地南偏东45°方向.现打算打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(结果精确到1千米)(参考数据:sin53°= ,cos53°= ,tan53°= )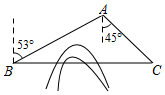 22. 小西想锻炼自己的生活能力,周末进行勤工俭学,他购进A、B两款摆件共100个,A、B两款摆件每个的成本和售价如表所示:
22. 小西想锻炼自己的生活能力,周末进行勤工俭学,他购进A、B两款摆件共100个,A、B两款摆件每个的成本和售价如表所示:A
B
成本(元/个)
3
3.5
售价(元/个)
3.6
4.3
设小西购进A款摆件个,每天两款摆件的总利润为元.(利润=售价-成本)
(1)、 与之间的函数关系式;(2)、如果小西每天要获得的总利润不低于70元,求他每天至多购进A款摆件的个数.23. 某校想要落实“二十大精神”,发展学生体质,为了了解学生“每天体育运动的时间”(简称“运动时间”)情况,在本校随机调查了50名学生的“运动时间”,并进行统计,绘制了如下统计表;组别
“运动时间”/分钟
频数
组内学生的平均“运动时间”/分钟
A
4
15
B
8
25
C
20
35
D
18
50
根据上述信息,解答下列问题:
(1)、这50名学生的“运动时间”的中位数落在组;(2)、求这50名学生的平均“运动时间”;(3)、若该校有3600名学生,请估计在该校学生中,“运动时间”不少于30分钟的人数.24. 如图,是的直径,射线交于点D,E是劣弧上一点,且 , 过点E作于点F,延长和的延长线交于点G. (1)、证明:是的切线;(2)、若 , , 求的长.25. 如图,抛物线与轴交于点和点 , 与轴交于点 . 抛物线的对称轴与轴交于点 .
(1)、证明:是的切线;(2)、若 , , 求的长.25. 如图,抛物线与轴交于点和点 , 与轴交于点 . 抛物线的对称轴与轴交于点 . (1)、求该抛物线的表达式;(2)、若点在抛物线的对称轴上,线段绕点顺时针旋转后,点的对应点恰好也落在此抛物线上,请求出所有满足条件的点的坐标.26. 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.如图,在矩形中, , .
(1)、求该抛物线的表达式;(2)、若点在抛物线的对称轴上,线段绕点顺时针旋转后,点的对应点恰好也落在此抛物线上,请求出所有满足条件的点的坐标.26. 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.如图,在矩形中, , .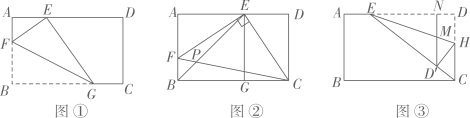 (1)、如图①,将矩形折叠,使顶点落在边上的点处,折痕的一端点在边上.当折痕的另一端点在边上,且时,的度数为;(2)、如图②,将矩形折叠,使顶点落在边上的点处,折痕的一端点在边上,另一端点为矩形的顶点 . 将折叠后重新展开,连接 , , 过点作交线段于点 , 连接 , 与交于点 . 求长;(3)、如图③,将沿直线折叠,连接 , 折叠后点落在边上的点处,点在边上,过点作于点 , 与交于点 , 且 . 求的面积.
(1)、如图①,将矩形折叠,使顶点落在边上的点处,折痕的一端点在边上.当折痕的另一端点在边上,且时,的度数为;(2)、如图②,将矩形折叠,使顶点落在边上的点处,折痕的一端点在边上,另一端点为矩形的顶点 . 将折叠后重新展开,连接 , , 过点作交线段于点 , 连接 , 与交于点 . 求长;(3)、如图③,将沿直线折叠,连接 , 折叠后点落在边上的点处,点在边上,过点作于点 , 与交于点 , 且 . 求的面积.