广东省深圳市南山区2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. ﹣3的相反数是( )A、 B、 C、-3 D、32. 5600万!梅西卡塔尔世界杯夺冠后的个人动态点赞数打破吉尼斯纪录,成历史第一.5600万用科学记数法表示( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由五个相同的小立方块搭成的几何体,这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 2021年7月24日,杨倩以251.8环的成绩获得2020年东京奥运会射击女子10米气步枪项目金牌,为中国队收获东京奥运会的首枚金牌.她的其中5个成绩(单位:环)分别是:9、8、9、9、10;关于这组数据,以下结论错误的是( )A、众数为9 B、中位数为9 C、平均数为9 D、方差为26. 将不等式组的解集在数轴上表示,正确的是( )A、
5. 2021年7月24日,杨倩以251.8环的成绩获得2020年东京奥运会射击女子10米气步枪项目金牌,为中国队收获东京奥运会的首枚金牌.她的其中5个成绩(单位:环)分别是:9、8、9、9、10;关于这组数据,以下结论错误的是( )A、众数为9 B、中位数为9 C、平均数为9 D、方差为26. 将不等式组的解集在数轴上表示,正确的是( )A、 B、
B、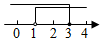 C、
C、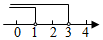 D、
D、 7. 若关于的一元二次方程有两个不相等的实数根、 , 则的值是( )A、 B、 C、 D、8. 下列说法正确的是( )A、两点之间,直线最短 B、线段垂直平分线上的点到这条线段两个端点的距离相等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、圆周角的度数等于圆心角度数的一半9. 南山文体中心打算购买李宁、安踏两种不同品牌的篮球,已知李宁篮球的单价是安踏篮球的单价的1.2倍,且用1200元购买的李宁篮球的数量比用1200元购买安踏篮球的数量少2个,设安踏篮球的单价为元,则下列方程正确的是( )A、 B、 C、 D、10. 如图,四边形中, , 以为直径的经过点C,连接、交于点.连接交于点 , 连接 , 若 , , 则以下结论:①;②为的切线;③;④;则正确的结论个数为( )
7. 若关于的一元二次方程有两个不相等的实数根、 , 则的值是( )A、 B、 C、 D、8. 下列说法正确的是( )A、两点之间,直线最短 B、线段垂直平分线上的点到这条线段两个端点的距离相等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、圆周角的度数等于圆心角度数的一半9. 南山文体中心打算购买李宁、安踏两种不同品牌的篮球,已知李宁篮球的单价是安踏篮球的单价的1.2倍,且用1200元购买的李宁篮球的数量比用1200元购买安踏篮球的数量少2个,设安踏篮球的单价为元,则下列方程正确的是( )A、 B、 C、 D、10. 如图,四边形中, , 以为直径的经过点C,连接、交于点.连接交于点 , 连接 , 若 , , 则以下结论:①;②为的切线;③;④;则正确的结论个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 分解因式:2a2+4a+2= .12. 从1~9这9个自然数中,任取一个,是3的倍数的概率是 .13. 如图,已知直线 , 的顶点在直线上, , , 则的度数是 .
 14. 如图,点在反比例函数的图象上,点在轴上,轴,点为轴上一点,过点作 , 交轴于点 , 若 , 则的值为 .
14. 如图,点在反比例函数的图象上,点在轴上,轴,点为轴上一点,过点作 , 交轴于点 , 若 , 则的值为 . 15. 如图所示, , , 以为底边向上构造等腰直角三角形 , 连接并延长至点P,使 , 则长的取值范围为 .
15. 如图所示, , , 以为底边向上构造等腰直角三角形 , 连接并延长至点P,使 , 则长的取值范围为 .
三、解答题
-
16. 计算: .17. 先化简,再求值: , 从 , , , , 中取一个合适的数作为的值代入求值.18. 某校校园文化节中组织全校学生进行知识竞赛,参赛学生均获奖.为了解本次竞赛获奖的分布情况,从中随机抽取了部分学生的获奖结果进行统计分析,获奖结果分为四个等级:级为特等奖,级为一等奖,级为二等奖,级为三等奖,将统计结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题:
 (1)、本次被抽取的部分人数是 ▲ 名,并把条形统计图补充完整;(2)、扇形统计图中表示级的扇形圆心角的度数是;(3)、根据抽样结果,请估计该校1800名学生获得特等奖的人数是名;(4)、调查数据中有3名获特等奖的学生甲、乙、丙,要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求丙被选中的概率.19. 开学季,某文具店购进甲、乙两种笔记本共100本,总成本为620元,两种笔记本的成本和售价如下表:
(1)、本次被抽取的部分人数是 ▲ 名,并把条形统计图补充完整;(2)、扇形统计图中表示级的扇形圆心角的度数是;(3)、根据抽样结果,请估计该校1800名学生获得特等奖的人数是名;(4)、调查数据中有3名获特等奖的学生甲、乙、丙,要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求丙被选中的概率.19. 开学季,某文具店购进甲、乙两种笔记本共100本,总成本为620元,两种笔记本的成本和售价如下表:笔记本
成本(元/本)
售价(元/本)
甲
5
8
乙
7
15
(1)、文具批发店购进甲、乙两种笔记本各多少本?(2)、该文具店觉得这两种笔记本很物销,准备再购进200本,但是成本不能超过1200元,则文具店第二次进货的最大利润是多少?20. 如图,抛物线经过点 , 点 , 且 . (1)、求抛物线的表达式;(2)、如图,点是抛物线的顶点,求的面积.21.
(1)、求抛物线的表达式;(2)、如图,点是抛物线的顶点,求的面积.21.如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
 (1)、试说明CE是⊙O的切线;(2)、若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;(3)、设点D是线段AC上任意一点(不含端点),连接OD,当CD+OD的最小值为6时,求⊙O的直径AB的长.22. 某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段进行了如下探究:(1)、【观察与猜想】如图1,在正方形中,点 , 分别是 , 上的两点,连接 , , , 则的值为;
(1)、试说明CE是⊙O的切线;(2)、若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;(3)、设点D是线段AC上任意一点(不含端点),连接OD,当CD+OD的最小值为6时,求⊙O的直径AB的长.22. 某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段进行了如下探究:(1)、【观察与猜想】如图1,在正方形中,点 , 分别是 , 上的两点,连接 , , , 则的值为; (2)、如图2,在矩形中, , , 点是上的一点,连接 , , , 则的值为;
(2)、如图2,在矩形中, , , 点是上的一点,连接 , , , 则的值为; (3)、【证明与理解】如图3,在矩形中, , , , 求的值;
(3)、【证明与理解】如图3,在矩形中, , , , 求的值; (4)、【知识点应用】如图4,在中, , , , 将沿翻折后得到 , 点在边上,点在边上, , 求的值.
(4)、【知识点应用】如图4,在中, , , , 将沿翻折后得到 , 点在边上,点在边上, , 求的值.