广东省江门市2023年中考三模数学试卷
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 若 , 则的值是( )A、 B、 C、2 D、-22. 2021年11月6日,台积电宣称2025年将量产2纳米芯片,2纳米就是0.000000002米,数据0.000000002用科学记数法表示是( )A、 B、 C、 D、3. 如图,下列几何体的左视图不是矩形的是( )A、
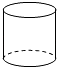 B、
B、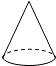 C、
C、 D、
D、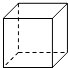 4. 下列计算正确的是( )A、 B、 C、 D、5. 已知直线 , 将一块含角的直角三角板按如图方式放置,其中直角顶点在直线上,斜边与直线交于的中点 , 连接 . 若 , 则的度数为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 已知直线 , 将一块含角的直角三角板按如图方式放置,其中直角顶点在直线上,斜边与直线交于的中点 , 连接 . 若 , 则的度数为( ) A、 B、 C、 D、6. 对于反比例函数 , 下列说法正确的是( )A、图象经过点 B、图象位于第二、第四象限 C、该函数与坐标轴不可能有交点 D、当时,随x的增大而增大7. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠18. 一组数据3,4,4,5,若添加一个数4,则发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差9. 如图,在直角坐标系中,菱形顶点A,B,C在坐标轴上,若点B的坐标为 , , 当恰好第一次落在线段上时,的坐标为( )
A、 B、 C、 D、6. 对于反比例函数 , 下列说法正确的是( )A、图象经过点 B、图象位于第二、第四象限 C、该函数与坐标轴不可能有交点 D、当时,随x的增大而增大7. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠18. 一组数据3,4,4,5,若添加一个数4,则发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差9. 如图,在直角坐标系中,菱形顶点A,B,C在坐标轴上,若点B的坐标为 , , 当恰好第一次落在线段上时,的坐标为( )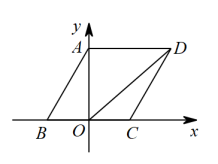 A、 B、 C、 D、10. 如图1,正方形ABCD中,动点P从点B出发,在正方形的边上沿B→C→D的方向匀速运动到点D停止,设点P的运动路程为x, , 图2是点P运动时y随x变化的关系图像,根据图中的数据,( )
A、 B、 C、 D、10. 如图1,正方形ABCD中,动点P从点B出发,在正方形的边上沿B→C→D的方向匀速运动到点D停止,设点P的运动路程为x, , 图2是点P运动时y随x变化的关系图像,根据图中的数据,( )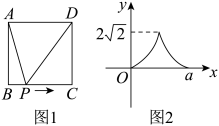 A、 B、4 C、 D、
A、 B、4 C、 D、二、填空题
-
11. 在函数中,自变量的取值范围是 .12. 已知x满足不等式组 , 则该不等式组的整数解的个数为 .13. 有背面完全相同,正面写有“十九届六中全会”字样的卡片n张,“元宇宙”字样的卡片4张,现正面朝下放置在桌面上,将其混合后,从中随机抽取一张,若抽中“十九届六中全会”字样的卡片的概率为 , 则 .14. 如图,已知扇形 , 点C为中点,点D在弧上,将扇形沿直线折叠,点A恰好落在点O,若 , , 则图中阴影部分的面积是 .
 15. 如图,在等腰三角形中, , , 点为的中点,点为边上一个动点,连接 , 点关于直线的对称点为点 , 分别连接 , , 当时,的长为 .
15. 如图,在等腰三角形中, , , 点为的中点,点为边上一个动点,连接 , 点关于直线的对称点为点 , 分别连接 , , 当时,的长为 .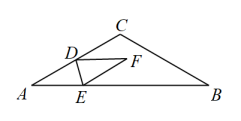
三、解答题
-
16. 先化简 , 然后从的范围内选一个你喜欢的整数作为的值代入求值.17. 为丰富师生的校园文化生活,激发师生热爱体育运动的兴趣,增强师生体质,营造奋进、和谐的校园氛围,年月日,商丘市梁园区某校举行了“趣味十一月”神采飞扬跳绳比赛活动.该校七年级采用随机抽签的方式选出了部分同学,并对这些同学一分钟跳绳的成绩进行了统计,绘制了如下统计图和统计表:
等级
次数
频数
不合格
合格
良好
优秀

请结合上述信息解决下列问题:
(1)、本次随机抽签的样本容量是;;(2)、请补全频数分布直方图;(3)、在扇形统计图中,“不合格”等级对应的圆心角的度数是;(4)、若该校有2800名学生,根据抽样调查结果,请估计该校学生一分钟跳绳成绩达到良好及以上的人数.18. 如图,在中, , 是斜边上的中线,以为直径的分别交于点M、N,交于点D、F(D、F可重合),过点N作 , 垂足为E. (1)、求证:;(2)、①当的度数为时,四边形为正方形;
(1)、求证:;(2)、①当的度数为时,四边形为正方形;②当的度数为时,四边形为菱形.
19. 如图,小明为测量宣传牌的高度 , 他站在距离建筑楼底部处6米远的地面处,测得宣传牌的底部的仰角为 . 同时测得建筑楼窗户处的仰角为(、、、在同一直线上).然后,小明沿坡度为的斜坡从走到处,此时正好与地面平行,若小明在处又测得宣传牌顶部的仰角为 , 求宣传牌的高度 . (结果精确到米, , )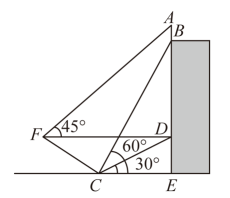 20. 2021年元月,国家发展改革委和生态环境部颁布的《关于进一步加强塑料污染治理的意见》正式实施,各大塑料生产企业提前做好了转型升级.红星塑料有限公司经过市场研究购进一批 型可降解聚乳酸吸管和一批 型可降解纸吸管生产设备.已知购买5台 型设备和3台 型设备共需130万元,购买1台 型设备的费用恰好可购买2台 型设备.
20. 2021年元月,国家发展改革委和生态环境部颁布的《关于进一步加强塑料污染治理的意见》正式实施,各大塑料生产企业提前做好了转型升级.红星塑料有限公司经过市场研究购进一批 型可降解聚乳酸吸管和一批 型可降解纸吸管生产设备.已知购买5台 型设备和3台 型设备共需130万元,购买1台 型设备的费用恰好可购买2台 型设备.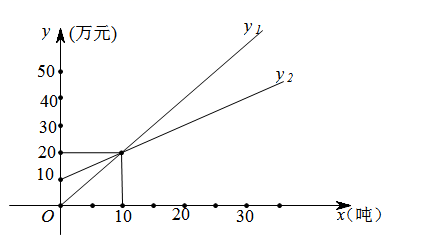 (1)、求两种设备的价格;(2)、市场开发部门经过研究,绘制出了吸管的销售收入与销售量(两种吸管总量)的关系(如 所示)以及吸管的销售成本与销售量的关系(如 所示).
(1)、求两种设备的价格;(2)、市场开发部门经过研究,绘制出了吸管的销售收入与销售量(两种吸管总量)的关系(如 所示)以及吸管的销售成本与销售量的关系(如 所示).① 的解析式为;
的解析式为.
②当销售量( )满足条件时,该公司盈利(即收入大于成本).
(3)、由于市场上可降解吸管需求大增,公司决定购进两种设备共10台,其中 型设备每天生产量为1.2吨, 型设备每天生产量为0.4吨,每天生产的吸管全部售出.为保证公司每天都达到盈利状态,结合市场开发部门提供的信息,求出 型设备至少需要购进多少台?21. 如图,半圆O中, , 点M为上一点, , 点P为半圆上一个动点,连接 , 过点A作 , 垂足为N.小明根据学习函数的经验,对线段的长度之间的关系进行了探究.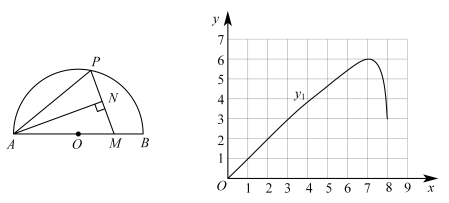
下面是小明的探究过程,请补充完整:
(1)、设的长度为 , 的长度为 , 的长度为 , 对于点P在半圆O上的不同位置,通过画图、测量,得到了线段的长度的几组值,如下表:/cm
0
1
2
3
4
5
6
7
7.5
7.64
7.78
7.90
8
/cm
0
0.99
1.99
2.97
3.92
4.82
5.61
5.90
5.56
5.18
4.46
3.30
0
/cm
6
5.91
5.65
5.21
4.53
3.56
2.12
0.24
2.25
3.01
4.0
5.00
6
请计算,当时,;
(2)、利用表格中的数据,在如平面直角坐标系中画出(1)中所确定的函数关于x的函数图象;(3)、观察函数图象分别写出函数、的一条性质;(4)、当等腰三角形时:①通过计算可知:;
②通过进一步探究函数图象可知:长度的近似值为 . (保留一位小数)
22. 如图,在平面直角坐标系中,直线与坐标轴交于两点,点在轴上,点在轴上, , 抛物线经过点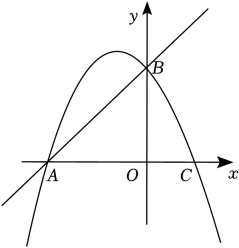 (1)、求抛物线的解析式;(2)、根据图象写出不等式的解集;(3)、点是抛物线上的一动点,过点作直线的垂线段,垂足为 , 当
(1)、求抛物线的解析式;(2)、根据图象写出不等式的解集;(3)、点是抛物线上的一动点,过点作直线的垂线段,垂足为 , 当时,求点的坐标.
23. 如图①,在菱形中, , , 连接 , 点在上的一点,连接交于点 , 过点作于点 , 连接 .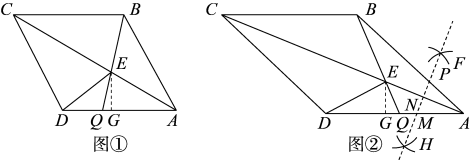 (1)、当且时, , ;(2)、当时,若时.求的长度;(3)、当时,如图②,分别以点 , 为圆心,大于的长为半径画弧.交于点和 , 作直线 , 分别交 , , 于点 , , , 请你判断点的位置是否变化?若不变,求的长;若变化说明理由.
(1)、当且时, , ;(2)、当时,若时.求的长度;(3)、当时,如图②,分别以点 , 为圆心,大于的长为半径画弧.交于点和 , 作直线 , 分别交 , , 于点 , , , 请你判断点的位置是否变化?若不变,求的长;若变化说明理由.