浙江省绍兴市城关“六校联考”2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
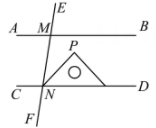
1. ( )A、 2023 B、 C、 D、2. 国家统计局网站公布我国2021年年末总人口约1412600000人,数据1412600000用科学记数法可以表示为( )A、14.126×108 B、1.4126×109 C、1.4126×108 D、0.14126×10103. 下列运算正确的是( )A、 B、 C、 D、4. 如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )
 A、15° B、25° C、35° D、45°5. 如图所示的几何体是由5个完全相同的小正方体组成,它的主视图是( )
A、15° B、25° C、35° D、45°5. 如图所示的几何体是由5个完全相同的小正方体组成,它的主视图是( )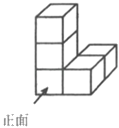 A、
A、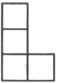 B、
B、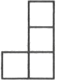 C、
C、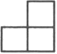 D、
D、 6. 如图所示, , , 要使 , 需添加条件是( )
6. 如图所示, , , 要使 , 需添加条件是( )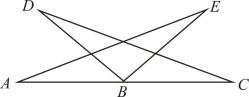 A、 B、 C、 D、7. 方程的解,可看成以下两个函数图象交点的横坐标,其中正确的个数是( )
A、 B、 C、 D、7. 方程的解,可看成以下两个函数图象交点的横坐标,其中正确的个数是( )①;②;③;④
A、4 B、3 C、2 D、18. 为迎接亚运,某校购买了一批篮球和足球,已知购买足球的数量是篮球的倍,购买足球用了元,购买篮球用了元,篮球单价比足球贵元,根据题意可列方程 , 则方程中关于的含义理解正确的是( )A、篮球有个 B、每个篮球元 C、足球有个 D、每个足球元9. 如图,已知直线:与轴,轴分别相交于点 , , 与直线相交于点 , 直线:与直线相交于点 , 与轴相交于点 . 已知 , , 当点从点运动到点的过程中,四边形的形状变化依次为( )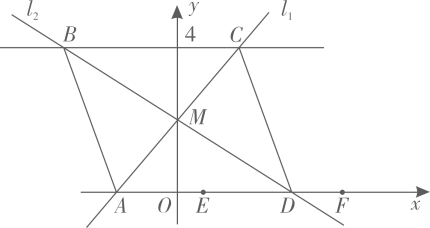 A、平行四边形→矩形→平行四边形→正方形→平行四边形 B、平行四边形→矩形→平行四边形→菱形→平行四边形 C、平行四边形→菱形→平行四边形→矩形→平行四边形 D、平行四边形→正方形→平行四边形→矩形→平行四边形10. 有9个形状大小相同的小球,其中一个略重些,其余8个重量相同.现给你一架天平,能将那个略重些的小球找到,则至少需要天平的次数是( )A、4 B、3 C、2 D、1
A、平行四边形→矩形→平行四边形→正方形→平行四边形 B、平行四边形→矩形→平行四边形→菱形→平行四边形 C、平行四边形→菱形→平行四边形→矩形→平行四边形 D、平行四边形→正方形→平行四边形→矩形→平行四边形10. 有9个形状大小相同的小球,其中一个略重些,其余8个重量相同.现给你一架天平,能将那个略重些的小球找到,则至少需要天平的次数是( )A、4 B、3 C、2 D、1二、填空题
-
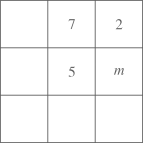
11. 分解因式: = .12. 关于x的不等式的解集是 .13. 幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方---九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则m的值为.
 14. 在菱形中,分别以点和点为圆心,大于为半径作弧,两弧交于点 , , 直线与直线交于点 , 且 , 则的值是 .15. 如图,等腰Rt△ABC的直角顶点B在y轴上,边AB交x轴于点D( ,0),点C的坐标为(﹣4,0),反比例函数y= (k≠0)的图象过点A,则k=.
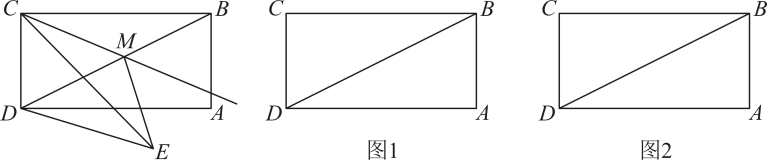
14. 在菱形中,分别以点和点为圆心,大于为半径作弧,两弧交于点 , , 直线与直线交于点 , 且 , 则的值是 .15. 如图,等腰Rt△ABC的直角顶点B在y轴上,边AB交x轴于点D( ,0),点C的坐标为(﹣4,0),反比例函数y= (k≠0)的图象过点A,则k=. 16. 如图,矩形中, , . 动点E在边上,以点E为圆心,以为半径作弧,点G是弧上一动点.
16. 如图,矩形中, , . 动点E在边上,以点E为圆心,以为半径作弧,点G是弧上一动点.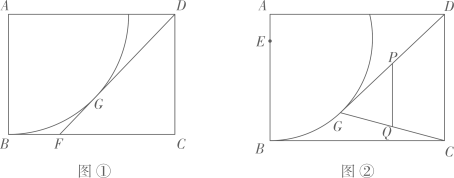 (1)、如图①,若点E与点A重合,且点F在上,当与弧相切于点G时,则的值是;(2)、如图②,若连结 , , 分别取、的中点P、Q , 连接 , M为的中点,则CM的最小值为 .
(1)、如图①,若点E与点A重合,且点F在上,当与弧相切于点G时,则的值是;(2)、如图②,若连结 , , 分别取、的中点P、Q , 连接 , M为的中点,则CM的最小值为 .三、解答题
-
17.(1)、计算:;(2)、解方程组18. 如图,在平行四边形中,E , F分别是边 , 上的点,且 .
 (1)、判定与是否相等,并说明理由;(2)、连接 , 若 , 求的度数.19. 我市有A , B , C , D , E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图:
(1)、判定与是否相等,并说明理由;(2)、连接 , 若 , 求的度数.19. 我市有A , B , C , D , E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图: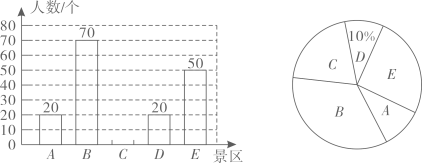 (1)、直接写出本次随机调查的总人数,并补全条形统计图;(2)、若该小区有居民1200人,试估计去B地旅游的居民约有多少人?(3)、小军同学已去过E地旅游,暑假期间计划与父母从A , B , C , D四个景区中,任选两个去旅游,求选到A , C两个景区的概率.(要求画树状图或列表求概率)20. 某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点O处,点O距地面的高度为 , 此时观测到楼底部点A处的俯角为 , 楼上点E处的俯角为 , 沿水平方向由点O飞行到达点F , 测得点E处俯角为 , 其中点A , B , C , D , E , F , O均在同一竖直平面内.(参考数据: , , , )
(1)、直接写出本次随机调查的总人数,并补全条形统计图;(2)、若该小区有居民1200人,试估计去B地旅游的居民约有多少人?(3)、小军同学已去过E地旅游,暑假期间计划与父母从A , B , C , D四个景区中,任选两个去旅游,求选到A , C两个景区的概率.(要求画树状图或列表求概率)20. 某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点O处,点O距地面的高度为 , 此时观测到楼底部点A处的俯角为 , 楼上点E处的俯角为 , 沿水平方向由点O飞行到达点F , 测得点E处俯角为 , 其中点A , B , C , D , E , F , O均在同一竖直平面内.(参考数据: , , , ) (1)、求的长;(2)、求楼与之间的距离的长.21. 如图,直线与相切于点C , 射线与交于点D , E , 连结 . 连结 .
(1)、求的长;(2)、求楼与之间的距离的长.21. 如图,直线与相切于点C , 射线与交于点D , E , 连结 . 连结 . (1)、求证:;(2)、若 , , 求弧的长.22. “五一”假期,甲乙两人沿同一条笔直的马路同时从同一小区出发到“三味书屋”参观,小区与“三味书屋”的路程是4千米,甲骑自行车,乙步行,当甲从原路回到小区时,乙刚好到达“三味书屋”,图中折线OABC和线段分别表示两人离小区的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据(图1)回答下列问题:
(1)、求证:;(2)、若 , , 求弧的长.22. “五一”假期,甲乙两人沿同一条笔直的马路同时从同一小区出发到“三味书屋”参观,小区与“三味书屋”的路程是4千米,甲骑自行车,乙步行,当甲从原路回到小区时,乙刚好到达“三味书屋”,图中折线OABC和线段分别表示两人离小区的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据(图1)回答下列问题: (1)、直接写出甲在“三味书屋”参观的时间;(2)、求图中点P(与交点)的坐标,并解释该点坐标所表示的实际意义;(3)、若两人之间的距离为y千米,当时,请在(图2)中画出y(千米)与所经过的时间t(分钟)之间的函数图象.
(1)、直接写出甲在“三味书屋”参观的时间;(2)、求图中点P(与交点)的坐标,并解释该点坐标所表示的实际意义;(3)、若两人之间的距离为y千米,当时,请在(图2)中画出y(千米)与所经过的时间t(分钟)之间的函数图象.