陕西省西安市阎良区2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 如图所示,将直尺与含角的直角三角板叠放在一起,若 , 则的度数为( )
 A、 B、 C、 D、3. 如图,数轴上两点 , 所对应的实数分别为 , , 则的结果可能是( )
A、 B、 C、 D、3. 如图,数轴上两点 , 所对应的实数分别为 , , 则的结果可能是( ) A、 B、 C、 D、4. 计算正确的结果是( )A、 B、 C、 D、5. 如图,在正方形中, , 点、分别是边、的中点,连接、 , 点 , 分别是 , 的中点,则的长为( )
A、 B、 C、 D、4. 计算正确的结果是( )A、 B、 C、 D、5. 如图,在正方形中, , 点、分别是边、的中点,连接、 , 点 , 分别是 , 的中点,则的长为( )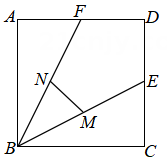 A、 B、 C、 D、26. 如图,在中,、是互相平行的弦,连接、、 , 若 . 则的度数为( )
A、 B、 C、 D、26. 如图,在中,、是互相平行的弦,连接、、 , 若 . 则的度数为( )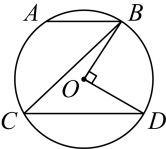 A、40° B、90° C、50° D、45°
A、40° B、90° C、50° D、45°二、解答题
-
7. 若抛物线与抛物线关于直线对称,则的值为( )A、3 B、7 C、 D、4
三、填空题
-
8. 在实数、、0、中,无理数有个.9. 如图, , 的坐标分别为 , . 若将线段平移至 , , 的坐标分别为 , , 则的值为 .
 10. 如图,在中, , 点在上,过点作的垂线 , 连接 , 若 , , , , 则的长为 .
10. 如图,在中, , 点在上,过点作的垂线 , 连接 , 若 , , , , 则的长为 .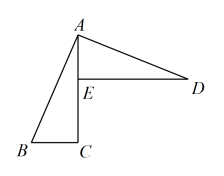 11. 《九章算术》是中国古代第一部数学专著,第一章“方田”中已讲述了平面图形面积的计算方法,比如扇形的计算,“今有宛田,下周三十步,径十六步,问为田几何?”大意为:现有一块扇形的田,弧长30步,其所在圆的直径是16步,则这块田的面积为平方步.
11. 《九章算术》是中国古代第一部数学专著,第一章“方田”中已讲述了平面图形面积的计算方法,比如扇形的计算,“今有宛田,下周三十步,径十六步,问为田几何?”大意为:现有一块扇形的田,弧长30步,其所在圆的直径是16步,则这块田的面积为平方步. 12. 如图,在平面直角坐标系中,A、B分别是x轴、y轴正半轴上的点,连接AB,反比例函数的图象经过线段AB的中点C,若 , 则的值为 .
12. 如图,在平面直角坐标系中,A、B分别是x轴、y轴正半轴上的点,连接AB,反比例函数的图象经过线段AB的中点C,若 , 则的值为 . 13. 如图,在菱形中, , , 点 , 分别在边 , 上,连接 , 点关于的对称点在线段上,则的最大值为 .
13. 如图,在菱形中, , , 点 , 分别在边 , 上,连接 , 点关于的对称点在线段上,则的最大值为 .
四、解答题
-
14. 计算: .15. 解不等式组: , 并把解集表示在数轴上.16. 解下列分式方程: .17. 如图,在中,于点 . 请用尺规作图法在上求作一点 , 使(不写作法,保留作图痕迹)
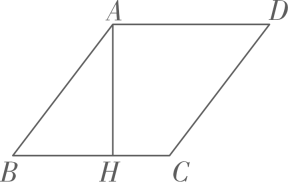 18. 如图,是的边的中点,连接、 , 且 , 求证:四边形是矩形.
18. 如图,是的边的中点,连接、 , 且 , 求证:四边形是矩形. 19. 如果一个正整数能表示为两个连续非负偶数的平方差,那么称这个正整数为“神秘数”,如: , .(1)、请你将20表示为两个连续非负偶数的平方差形式:;(2)、试证明“神秘数”能被4整除.20. 如图,在中, , 求BC的长.
19. 如果一个正整数能表示为两个连续非负偶数的平方差,那么称这个正整数为“神秘数”,如: , .(1)、请你将20表示为两个连续非负偶数的平方差形式:;(2)、试证明“神秘数”能被4整除.20. 如图,在中, , 求BC的长. 21. 中国-中亚峰会于5月18日至19日在陕西省西安市举行,让千年古都再次聚焦世界的目光,也让每一个西安人、陕西人感到骄傲.在一个不透明的口袋里,装有分别标着汉字“喜”、“迎”、“中”、“亚”、“峰”、“会”的六个小球,将其搅匀.这些小球除汉字不同外其它都相同.(1)、若从袋中任取一个小球,则取到的小球上的汉字恰好是“亚”的概率为;(2)、从袋中任取一个小球,不放回,搅匀后再从剩下的五个小球中任取一个,请用画树状图或列表法,求取到的两个小球上的汉字恰能组成“喜迎”或“中亚”或“峰会”的概率.(汉字不分先后顺序)22. 西安古城墙凝聚了中国古代劳动人民的智慧,它作为古城西安的地标性建筑,吸引了不少人慕名而来.节假日,乐乐去城墙游玩,看见宏伟的城墙后,他想要测量城墙的高度 . 如图,他拿着一根笔直的小棍 , 站在距城墙约30米的点N处(即米),把手臂向前伸直且让小棍竖直, , 乐乐看到点B和城墙顶端D在一条直线上,点C和底端E在一条直线上.已知乐乐的臂长约为60厘米,小棍的长为24厘米, , , , 求城墙的高度 .
21. 中国-中亚峰会于5月18日至19日在陕西省西安市举行,让千年古都再次聚焦世界的目光,也让每一个西安人、陕西人感到骄傲.在一个不透明的口袋里,装有分别标着汉字“喜”、“迎”、“中”、“亚”、“峰”、“会”的六个小球,将其搅匀.这些小球除汉字不同外其它都相同.(1)、若从袋中任取一个小球,则取到的小球上的汉字恰好是“亚”的概率为;(2)、从袋中任取一个小球,不放回,搅匀后再从剩下的五个小球中任取一个,请用画树状图或列表法,求取到的两个小球上的汉字恰能组成“喜迎”或“中亚”或“峰会”的概率.(汉字不分先后顺序)22. 西安古城墙凝聚了中国古代劳动人民的智慧,它作为古城西安的地标性建筑,吸引了不少人慕名而来.节假日,乐乐去城墙游玩,看见宏伟的城墙后,他想要测量城墙的高度 . 如图,他拿着一根笔直的小棍 , 站在距城墙约30米的点N处(即米),把手臂向前伸直且让小棍竖直, , 乐乐看到点B和城墙顶端D在一条直线上,点C和底端E在一条直线上.已知乐乐的臂长约为60厘米,小棍的长为24厘米, , , , 求城墙的高度 .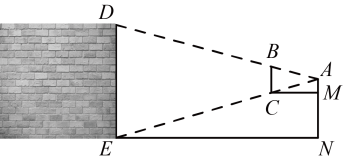 23. “盛唐密盒”的即兴表演和互动深度融合了中国的历史文化知识,让观众在互动答题的同时,也普及了传统文化知识,也显得更加“中国”,深受广大游客的喜欢.为弘扬中华优秀传统文化,某校学生处进行了《传统文化知识》5题问答测试,随机抽取了部分学生的答题情况,并把答对题数分别制成如下的统计表和扇形统计图.
23. “盛唐密盒”的即兴表演和互动深度融合了中国的历史文化知识,让观众在互动答题的同时,也普及了传统文化知识,也显得更加“中国”,深受广大游客的喜欢.为弘扬中华优秀传统文化,某校学生处进行了《传统文化知识》5题问答测试,随机抽取了部分学生的答题情况,并把答对题数分别制成如下的统计表和扇形统计图.答对题数
0
1
2
3
4
5
人数(人)
1
2
5
3
1

请根据统计图表中的信息,解答下列问题:
(1)、表中 , 所抽取学生答对题数的中位数是题,众数是题;(2)、求所抽取学生答对题数的平均数;(3)、若该校共有800名学生,根据抽查结果,估计该校学生答对5题的人数.24. 近年来,我国着力促进教育公平,提升教育质量,加快推进教育现代化、建设教育强国、办好人民满意的教育,教育数字化工作持续推进、成果丰硕.在教育数字化进程中,多媒体的作用不可小觑.某教育科技公司销售 , 两种多媒体教学设备,这两种多媒体设备的进价与售价如表所示:A
B
进价(万元/套)
3
2.4
售价(万元/套)
3.3
2.8
该教育科技公司计划购进 , 两种多媒体设备共套,设购进种多媒体设备x套,利润为y万元
(1)、求与之间的函数关系式;(2)、若公司要求购进种多媒体设备的数量不超过种多媒体设备的倍,当该公司把购进的两种多媒体设备全部售出,求购进种多媒体设备多少套时,能获得最大利润,最大利润是多少万元?25. 如图,四边形内接于 , 连接、交于点 , 是的直径,且 , 过点作的切线,交的延长线于点 . (1)、求证:;(2)、若 , , 求的长.26. 如图,在平面直角坐标系中,抛物线与轴交于、两点(在的左侧),与轴交于点.
(1)、求证:;(2)、若 , , 求的长.26. 如图,在平面直角坐标系中,抛物线与轴交于、两点(在的左侧),与轴交于点. (1)、求点、、的坐标;(2)、点在坐标平面内,在抛物线上是否存在点 , 使得以、、、为顶点的四边形是以为边且面积为12的平行四边形?若存在,求出点的坐标;若不存在,请说明理由.27.(1)、问题提出
(1)、求点、、的坐标;(2)、点在坐标平面内,在抛物线上是否存在点 , 使得以、、、为顶点的四边形是以为边且面积为12的平行四边形?若存在,求出点的坐标;若不存在,请说明理由.27.(1)、问题提出如图1,在中,于点 , 于点 , 若 , , 求的值;
 (2)、问题探究
(2)、问题探究如图2,在矩形中,点、分别在边、上,连接、 , 且 . 求证:;

问题解决
(3)、问题探究如图3,某地有一足够大的空地,现想在这片空地上修建一个平行四边形状的休闲区 , 其中 , 点、、分别在边、、上,管理部门欲从到、到分别修建小路,两条小路、交汇于点 , 且满足 , , 为使美观现要沿平行四边形的四条边修建绿化带(宽度忽略不计),求所修绿化带的长度(的周长).

-