陕西省宝鸡市陇县2023年中考三模数学试题

试卷更新日期：2023-06-14 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，是负数的是（）

A、 $| - 2 |$ B、 $- \frac{1}{6}$ C、0 D、3

查看试题解析
2. 下列展开图中，是正方体展开图的是（）

A、 B、 C、 D、

查看试题解析
3. 纳米科技是新兴科技，1纳米=0.000000001米，则5纳米用科学记数法表示为（）

A、 $5 \times 10^{- 8}$ 米 B、 $5 \times 10^{- 9}$ 米 C、 $5 \times 10^{- 10}$ 米 D、 $5 \times 10^{9}$ 米

查看试题解析
4. 下列式子计算结果等于 $- a^{5}$ 的是（）

A、 $- a^{3} + a^{2}$ B、 $- a^{10} \div a^{2}$ C、 ${(- a^{2})}^{3}$ D、 $(- a^{3}) \cdot a^{2}$

查看试题解析
5. 如图，长方体的底面边长分别为 $2$ 厘米和 $4$ 厘米，高为 $5$ 厘米.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为（）厘米

A、8 B、10 C、12 D、13

查看试题解析
6. 若不等式 $a x + b > 0$ 的解集是 $x < 3$ ，则下列各点可能在一次函数 $y = a x + b$ 的图象上的是（）

A、 $(1 ， 2)$ B、 $(4 ， 1)$ C、 $(- 1 ， - 3)$ D、 $(2 ， - 3)$

查看试题解析
7. 如图，在 $⊙ O$ 中， $O A ⊥ B C ， ∠ C D A = 22.5 °$ ，则 $∠ A O B$ 的度数为（）

A、 $22.5 °$ B、 $30 °$ C、 $45 °$ D、 $60 °$

查看试题解析
8. 二次函数 $y = {(x + m)}^{2} + n$ 的图像如图所示，则点 $(m ， n)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

二、填空题

9. 分解因式： $a^{2} b^{3} - 2 a b^{2} =$ ．

查看试题解析
10. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 上的高，E是 $A B$ 边的中点，连接 $D E$ ，若 $A B = B C = 6$ ， $∠ B =60 °$ ，则 $D E =$ ．

查看试题解析
11. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作，其中有一个数学问题：“直田积八百九十一步，只云长阔共六十步，问长多阔几何”．意思是：一块矩形田地的面积为891平方步，只知道它的长与宽共60步，问它的长比宽多多少步？根据题意得，长比宽多步．

查看试题解析
12. 如图，一次函数 $y = k x$ 与反比例函数 $y = \frac{k}{x}$ 上的图象交于A，C两点， $A B ∥ y$ 轴， $B C ∥ x$ 轴，若 $△ A B C$ 的面积为4，则 $k =$ ．

查看试题解析
13. 如图，已知在矩形 $A B C D$ 中，点 $E$ 在边 $B C$ 上， $B E = 2 C E$ ，将矩形沿着过点 $E$ 的直线翻折后，点 $C ， D$ 分别落在边 $B C$ 下方的点 $C^{'} ， D^{'}$ 处，且点 $C^{'} ， D^{'} ， B$ 在同一条直线上，折痕与边 $A D$ 交于点 $F ， D^{'} F$ 与 $B E$ 交于点 $G$ ．设 $A B = \sqrt{3}$ ，那么 $△ E F G$ 的周长为．

查看试题解析

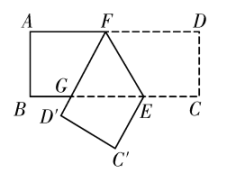
三、解答题

14. 计算： $4 sin 60 ° - | 2 - \sqrt{3} | - {(2023 - π)}^{0}$ ．

查看试题解析
15. 解不等式组： ${\begin{array}{l} 4 x - 2 \leq 3 (x + 1) \\ 1 - \frac{x - 1}{2} < \frac{x}{4} \end{array}$ ．

查看试题解析
16. 解分式方程： $\frac{x}{x^{2} - 1} + 1 = \frac{x}{x + 1}$ ．

查看试题解析
17. 如图所示，请用尺规作图法，在矩形 $A B C D$ 的边 $B C$ 上确定一点 $E$ ，使得 $A B = \frac{1}{2} A E$ ．

查看试题解析
18. 如图，点B ， E ， C ， F在一条直线上， $A C$ 与 $D E$ 相交于点O ，已知 $A B = D E$ ， $A B ∥ D E$ ， $A C ∥ D F$ ．求证： $△ A B C ≌ △ D E F$ ．

查看试题解析
19. 如图，在边长为1的正方形网格中建立平面直角坐标系，已知 $△ A B C$ 三个顶点分别为 $A (- 1 ， 2) 、 B (2 ， 1) 、 C (4 ， 5)$ ．

(1)、以原点O为位似中心，在x轴的上方画出 $△ A_{1} B_{1} C_{1}$ ，使 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 位似，且相似比为 $2 ： 1$ ；

(2)、 $△ A_{1} B_{1} C_{1}$ 的面积为．

查看试题解析
20. 张洋所住小区的每栋楼下均设有供业主使用的公共底面停车场，这天他放学回家时观察到位于他家楼下的停车场还剩余四个车位，小区规定每辆汽车停放时只能占用一个车位．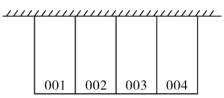

(1)、若此时有一辆汽车停车，则这辆车停在“003”号车位的概率是；

(2)、若此时有两辆汽车同时停车，求这两辆车停在相邻车位的概率．

查看试题解析
21. 某校九年级一班的兴趣小组准备测量学校外一栋建筑 $M N$ 物的高度，出于安全考虑，他们不得离开校园，于是便利用所学知识制定了如下的测量方案：如图所示，首先，王磊站在点 $B$ ，并在正前方 $3$ 米的点 $C$ 放置一平面镜，通过平面镜王磊刚好可以看到建筑物的顶端点 $M$ ，此时测得王磊的眼睛到地面的距离 $A B$ 为 $1.5$ 米；然后，刘慧在建筑物的影子顶端 $D$ 点竖立了一根高 $2$ 米的标杆 $D E$ ，此时测得标杆的影子 $D F$ 长为 $6$ 米，而王磊与刘慧之间的距离 $B D$ 为 $61$ 米，已知 $M N ⊥ N F$ ， $A B ⊥ N F$ ， $E D ⊥ N F$ ，点 $N$ ， $C$ ， $B$ ， $F$ ， $D$ 在一条直线上，请根据以上数据，计算目标建筑物 $M N$ 的高度 $($ 平面镜大小忽略不计 $)$ ．

查看试题解析
22. 我国新疆地区种植的棉花以绒长、品质好、产量高闻名世界．研究表明，在棉花成长周期内，随着棉花的不断成熟，成长高度y（cm）与成长时间x（天）的函数关系如图所示．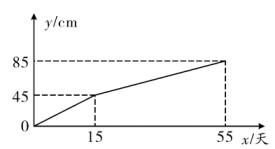

(1)、求y与x的函数关系式．

(2)、棉花在成长过程中，第25天时，开始进入吐絮期．试求出第25天时，棉花成长的高度．

查看试题解析
23. 3月21日是世界睡眠日，为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组： $x < 8.5$ ；B组： $8.5 \leq x < 9$ ；C组： $9 \leq x < 9.5$ ；D组： $9.5 \leq x < 10$ ；E组： $x \geq 10$ ．根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：

(1)、补全条形统计图，在扇形统计图中，D组所对应的扇形圆心角的度数为°；

(2)、本次抽样调查的中位数落在组，众数落在组；

(3)、若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人．

查看试题解析
24. 如图， $△ A B C$ 内接于 $⊙ O$ ，延长直径 $A B$ 到D ，使 $∠ B C D = ∠ B A C$ ，过圆心O作 $B C$ 的平行线交 $D C$ 的延长线于点E ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线；

(2)、若 $C D = 4 ， C E = 6$ ，求 $⊙ O$ 的半径．

查看试题解析
25. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $A (1 ， 0)$ ， $B (3 ， 0)$ 与 $y$ 轴正半轴交于点 $C$ ，连接 $A C$ ， $tan ∠ O A C = 3$ ．

(1)、求二次函数的表达式；

(2)、若x轴上有一点 $D$ 从 $(- 4 ， 0)$ 出发，沿 $x$ 轴正方向平移，平移距离为 $m$ （ $m > 0$ ），是否存在点 $D$ 使得 $△ A C D$ 是等腰三角形，若存在，请求出 $m$ 的值．若不存在请说明理由．

查看试题解析
26. 在学习对称的知识点时，我们认识了如下图所示的“将军饮马”模型求最短距离．

(1)、问题提出：
如图1所示，已知A ， B是直线l同旁的两个定点．在直线l上确定一点P ，并连接 $A P$ 与 $B P$ ，使 $P A + P B$ 的值最小．

(2)、问题探究：
如图2所示，正方形 $A B C D$ 的边长为2，E为 $A B$ 的中点，P是 $A C$ 上一动点．连接 $E P$ 和 $B P$ ，则 $P B + P E$ 的最小值是；

(3)、问题解决：
某地有一如图3所示的三角形空地 $A O B$ ，已知 $∠ A O B = 45 °$ ， P是 $△ A O B$ 内一点，连接 $P O$ 后测得 $P O = 10$ 米，现当地政府欲在三角形空地 $A O B$ 中修一个三角形花坛 $P Q R$ ，点 $Q ， R$ 分别是 $O A ， O B$ 边上的任意一点（不与各边顶点重合），求 $△ P Q R$ 周长的最小值．

查看试题解析