江苏省徐州市沛县2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 2023的相反数是( )A、2023 B、 C、-2023 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、a+2a=3a2 B、(a2)3=a5 C、a3·a4=a12 D、(-3a)2= 9a24. 如图,是由相同大小的五个小正方体组成的立体模型,它的俯视图是( )
3. 下列运算正确的是( )A、a+2a=3a2 B、(a2)3=a5 C、a3·a4=a12 D、(-3a)2= 9a24. 如图,是由相同大小的五个小正方体组成的立体模型,它的俯视图是( ) A、
A、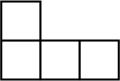 B、
B、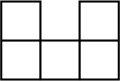 C、
C、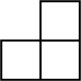 D、
D、 5. 下列语句所描述的事件是随机事件的是( )A、两点决定一直线 B、清明时节雨纷纷 C、没有水分,种子发芽 D、太阳从东方升起6. 某校为增强学生的爱国意识,特开展中国传统文化知识竞赛,九年级共30人参加竞赛,得分情况如下表所示,则这些成绩的中位数和众数分别是( )
5. 下列语句所描述的事件是随机事件的是( )A、两点决定一直线 B、清明时节雨纷纷 C、没有水分,种子发芽 D、太阳从东方升起6. 某校为增强学生的爱国意识,特开展中国传统文化知识竞赛,九年级共30人参加竞赛,得分情况如下表所示,则这些成绩的中位数和众数分别是( )成绩/分
90
92
94
96
100
人数/人
2
4
9
10
5
A、94分,96分 B、95分,96分 C、96分,96分 D、96分,100分7. 如图,在平面直角坐标系中,点A的坐标为(-1,),以原点O为中心,将点A顺时针旋转90°得到点 , 则点坐标为( ) A、(1,−) B、(− , 1) C、(0,2) D、( , 1)8. 如图,、两点分别在函数和的图象上,线段轴,点在轴上,则的面积为( )
A、(1,−) B、(− , 1) C、(0,2) D、( , 1)8. 如图,、两点分别在函数和的图象上,线段轴,点在轴上,则的面积为( ) A、3 B、4 C、6 D、9
A、3 B、4 C、6 D、9二、填空题
-
9. 64的平方根是 .10. 要使式子 有意义,则x的取值范围是 .11. 分解因式: =.
12. 根据电影发行方的数据,电影《满江红》截至2023年3月17日,以4535000000元的票房高居春节档前列,数据4535000000用科学记数法表示为 .13. 已知关于x的一元二次方程有两个实数根,则实数k的取值范围是 .14. 已知点 , 在一次函数的图象上,则mn(填“>”“=”或“<”).15. 如图,在中,弦 , 相较于点 , , , 则的大小是度. 16. 中国扇文化有着深厚的民族文化底蕴.如图,一扇形纸扇长为 , 贴画部分的宽为 . 该纸扇完全打开后,扇子外侧和所成的角为 , 则贴画一面的面积为(结果保留).
16. 中国扇文化有着深厚的民族文化底蕴.如图,一扇形纸扇长为 , 贴画部分的宽为 . 该纸扇完全打开后,扇子外侧和所成的角为 , 则贴画一面的面积为(结果保留). 17. 如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点 . 若 , , , 则的长为 .
17. 如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点 . 若 , , , 则的长为 . 18. 如图由内角分别相等的四边形、五边形、六边形组合而成的图形中, , 则的度数为度.
18. 如图由内角分别相等的四边形、五边形、六边形组合而成的图形中, , 则的度数为度.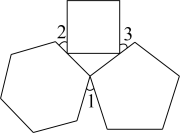
三、解答题
-
19. 计算:(1)、(2)、20.(1)、解方程: .(2)、解不等式组: .21. 中国共产党第二十次全国代表大会于2022年10月16日在北京召开.在会议召开期间,国家领导人就许多民众关心的热点问题进行了时论,并形成了许多的决议.为了了解民众对“二十大”相关政策的了解情况,某小区居民进行了随机抽样调查,选取其中五个热点议题的关键词,分别为:“A . 依法治国;B . 社会保障;C . 乡村振兴;D . 教育改革;E . 数字化生活”,每人只能从中选一个最关注的议题,根据调查结果绘制了两幅不完整的统计图,请结合统计图中的信息,解决下列问题:
 (1)、图中B所在扇形的圆心角度数为;(2)、扇形统计图中,;(3)、将条形统计图补充完整;(4)、若这个小区居民共有1300人,根据抽样调查的结果,估计该小区居民中最关注的议题是“教育改革”的大约有多少人?22. 第二十四届冬雪大会于2022年2月20日在北京闭幕,北京成为全球首个既举办过夏季奥运会又举办过冬季奥运会的城市.有四张关于冬奥会运动项目的卡片,卡片的正面分别印有A . “花样滑冰”,B . “高山滑雪”,C . “单板滑雪大跳台”,D . “钢架雪车”,(这四张卡片除正面图案外,其余都相同).将这四张卡片背面朝上,洗匀.
(1)、图中B所在扇形的圆心角度数为;(2)、扇形统计图中,;(3)、将条形统计图补充完整;(4)、若这个小区居民共有1300人,根据抽样调查的结果,估计该小区居民中最关注的议题是“教育改革”的大约有多少人?22. 第二十四届冬雪大会于2022年2月20日在北京闭幕,北京成为全球首个既举办过夏季奥运会又举办过冬季奥运会的城市.有四张关于冬奥会运动项目的卡片,卡片的正面分别印有A . “花样滑冰”,B . “高山滑雪”,C . “单板滑雪大跳台”,D . “钢架雪车”,(这四张卡片除正面图案外,其余都相同).将这四张卡片背面朝上,洗匀. (1)、从中随机抽取一张,抽得的卡片恰好为“花样滑冰”的概率为;(2)、若从中随机抽取两张卡片,请你用列表或画树状图的方法,求抽取的卡片中有“高山滑雪”的概率.23. 如图,在平行四边形中,过点作于点点在边上,连接AF,BF.
(1)、从中随机抽取一张,抽得的卡片恰好为“花样滑冰”的概率为;(2)、若从中随机抽取两张卡片,请你用列表或画树状图的方法,求抽取的卡片中有“高山滑雪”的概率.23. 如图,在平行四边形中,过点作于点点在边上,连接AF,BF.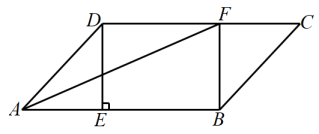 (1)、求证:四边形是矩形;(2)、若平分求四边形的面积.24. 如图,为等腰三角形, , O是底边的中点,⊙O与腰相切于点D .
(1)、求证:四边形是矩形;(2)、若平分求四边形的面积.24. 如图,为等腰三角形, , O是底边的中点,⊙O与腰相切于点D . (1)、求证:与⊙O相切;(2)、已知半径为 , , 求阴影部分的面积.25. 端午节吃粽子是中华民族的传统习俗.某超市节前购进了甲、乙两种畅销口味的粽子.已知购进甲种粽子的金额是1200元,购进乙种粽子的金额是800元,购进甲种粽子的数量比乙种粽子的数量少50个,甲种粽子的单价是乙种粽子单价的2倍.求乙种粽子的单价是多少元?26. 一个无盖的长方体盒子的展开图如图所示.
(1)、求证:与⊙O相切;(2)、已知半径为 , , 求阴影部分的面积.25. 端午节吃粽子是中华民族的传统习俗.某超市节前购进了甲、乙两种畅销口味的粽子.已知购进甲种粽子的金额是1200元,购进乙种粽子的金额是800元,购进甲种粽子的数量比乙种粽子的数量少50个,甲种粽子的单价是乙种粽子单价的2倍.求乙种粽子的单价是多少元?26. 一个无盖的长方体盒子的展开图如图所示. (1)、该盒子的底面的长为(用含a的式子表示).(2)、若①,②,③,④四个面上分别标有整式 , x , , 4,且该盒子的相对两个面上的整式的和相等,求x的值.(3)、请在图中补充一个长方形,使该展开图折叠成长方体盒子后有盖.27. 科技改变生活,科技服务生活.如图为一新型可调节洗手装置侧面示意图,可满足不同人的洗手习惯,为竖直的连接水管,当出水装置在A处且水流与水平面夹角为时,水流落点正好为水盆的边缘C处;将出水装置水平移动至B处且水流与水平面夹角为30°时,水流落点正好为水盆的边缘D处, .
(1)、该盒子的底面的长为(用含a的式子表示).(2)、若①,②,③,④四个面上分别标有整式 , x , , 4,且该盒子的相对两个面上的整式的和相等,求x的值.(3)、请在图中补充一个长方形,使该展开图折叠成长方体盒子后有盖.27. 科技改变生活,科技服务生活.如图为一新型可调节洗手装置侧面示意图,可满足不同人的洗手习惯,为竖直的连接水管,当出水装置在A处且水流与水平面夹角为时,水流落点正好为水盆的边缘C处;将出水装置水平移动至B处且水流与水平面夹角为30°时,水流落点正好为水盆的边缘D处, . (1)、求连接水管的长.(结果保留整数)(2)、求水盆两边缘C , D之间的距离.(结果保留一位小数)
(1)、求连接水管的长.(结果保留整数)(2)、求水盆两边缘C , D之间的距离.(结果保留一位小数)(参考数据:)
28. 如图,在平面直角坐标系中,抛物线与x轴交于两点(点A在点B的左侧),与y轴交于点C,连接 , 点P为直线上方抛物线上一动点,连接交于点Q. (1)、求抛物线的函数表达式;(2)、当的值最大时,求点P的坐标和的最大值;(3)、把抛物线向右平移1个单位,再向上平移2个单位得新抛物线 , M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,写出所有符合条件的N点的坐标,并写出求解点N的坐标的其中一种情况的过程.
(1)、求抛物线的函数表达式;(2)、当的值最大时,求点P的坐标和的最大值;(3)、把抛物线向右平移1个单位,再向上平移2个单位得新抛物线 , M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,写出所有符合条件的N点的坐标,并写出求解点N的坐标的其中一种情况的过程.