2023年江苏省无锡市中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 下列图案中是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图是由5个相同的小立方体搭成的几何体,它的主视图是( )
2. 如图是由5个相同的小立方体搭成的几何体,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 已知 是不等式 的解,b的值可以是( )A、4 B、2 C、0 D、4. 若正多边形的一个外角是 , 则该正多边形的边数是( )A、3 B、4 C、5 D、65. 下列说法正确的是( )A、任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件 B、某市天气预报明天的降水概率为90%,则“明天下雨”是确定事件 C、小丽买一张体育彩票中“一等奖”是随机事件 D、若a是实数,则“|a|≥0”是不可能事件6. 下列函数的图象在每一个象限内,y值随x值的增大而增大的是( )A、y=-x+1 B、 C、 D、7.
3. 已知 是不等式 的解,b的值可以是( )A、4 B、2 C、0 D、4. 若正多边形的一个外角是 , 则该正多边形的边数是( )A、3 B、4 C、5 D、65. 下列说法正确的是( )A、任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件 B、某市天气预报明天的降水概率为90%,则“明天下雨”是确定事件 C、小丽买一张体育彩票中“一等奖”是随机事件 D、若a是实数,则“|a|≥0”是不可能事件6. 下列函数的图象在每一个象限内,y值随x值的增大而增大的是( )A、y=-x+1 B、 C、 D、7.一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
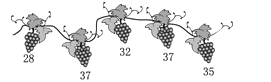 A、37 B、35 C、33.8 D、328. 一块直角边分别为6和8的三角形木板,绕长度为8的边旋转一周,则斜边扫过的面积是( )A、45 B、 C、60 D、9. 如图, 是 直径,点C、D将 分成相等的三段弧,点P在 上.已知点Q在 上且 ,则点Q所在的弧是( )
A、37 B、35 C、33.8 D、328. 一块直角边分别为6和8的三角形木板,绕长度为8的边旋转一周,则斜边扫过的面积是( )A、45 B、 C、60 D、9. 如图, 是 直径,点C、D将 分成相等的三段弧,点P在 上.已知点Q在 上且 ,则点Q所在的弧是( )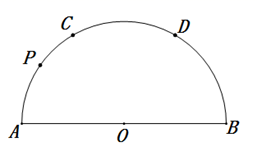 A、 B、 C、 D、10. 如图1,有一张矩形纸片 , 已知 , 现将纸片进行如下操作:现将纸片沿折痕进行折叠,使点落在边上的点处,点在上(如图2);然后将纸片沿折痕进行第二次折叠,使点落在第一次的折痕上的点处,点在上(如图3),给出四个结论:①的长为;②的周长为;③;④的长为 , 其中所有正确的结论有( )
A、 B、 C、 D、10. 如图1,有一张矩形纸片 , 已知 , 现将纸片进行如下操作:现将纸片沿折痕进行折叠,使点落在边上的点处,点在上(如图2);然后将纸片沿折痕进行第二次折叠,使点落在第一次的折痕上的点处,点在上(如图3),给出四个结论:①的长为;②的周长为;③;④的长为 , 其中所有正确的结论有( ) A、①③ B、①④ C、①③④ D、①②③④
A、①③ B、①④ C、①③④ D、①②③④二、填空题
-
11. 分解因式:2x2﹣8=12. 若的值为有理数,请你写出一个符合条件的实数a的值 .13. “神舟”五号飞船总重7990000克,用科学记数法表示为克.14. 如图,在一束平行光线中插入一张对边平行的纸板.如果图中 是 ,那么 的度数是 .
 15. 函数的图象与直线y=x没有交点,那么m的取值范围是 .16. 已知 ,则x﹣y= .17. 若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:、都是“整点”,抛物线()与轴交于A、B两点,若该抛物线在A、B之间的部分与线段所围成的区域(包括边界)恰有6个整点,则m的取值范围是 .18. 如图,在直角坐标系中, , D是上一点,B是y正半轴上一点,且 , , 垂足为E ,
15. 函数的图象与直线y=x没有交点,那么m的取值范围是 .16. 已知 ,则x﹣y= .17. 若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:、都是“整点”,抛物线()与轴交于A、B两点,若该抛物线在A、B之间的部分与线段所围成的区域(包括边界)恰有6个整点,则m的取值范围是 .18. 如图,在直角坐标系中, , D是上一点,B是y正半轴上一点,且 , , 垂足为E ,
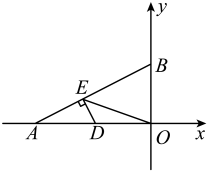 (1)、当D是的中点时,;(2)、求的最小值
(1)、当D是的中点时,;(2)、求的最小值三、解答题
-
19. 计算:(1)、(2)、20.(1)、解方程:;(2)、解不等式组:21. △ABC中,D、E分别为AB、AC的中点,F为EC的中点,BC、DF的延长线交于点G.
 (1)、求证:△DEF≌△GCF;(2)、求证:BC=2CG.22. 某校组织了由九年级700名学生参加的党史知识竞赛.丁老师随机抽取了部分向学的成绩作为样本,把成绩按优秀、良好、及格、不及格4个级别进行统计,并绘制成了如图的条形统计图和扇形统计图(部分信息未给出).
(1)、求证:△DEF≌△GCF;(2)、求证:BC=2CG.22. 某校组织了由九年级700名学生参加的党史知识竞赛.丁老师随机抽取了部分向学的成绩作为样本,把成绩按优秀、良好、及格、不及格4个级别进行统计,并绘制成了如图的条形统计图和扇形统计图(部分信息未给出).
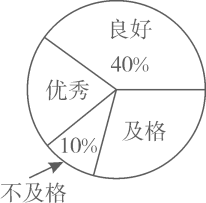
请根据以上提供的信息,解答下列问题:
(1)、求被抽取的部分学生的人数;(2)、请补全条形统计图,并求出扇形统计图中表示及格的扇形的圆心角度数;(3)、请估计九年级参加知识竞赛的700名学生中达到良好和优秀的总人数.23. 2023年春节档电影票房火爆,电影《流浪地球2》和《满江红》深受观众喜爱,甲、乙、丙三人从这两部电影中任意选择一部观看.(1)、甲选择《流浪地球2》的概率是;(2)、求甲、乙、丙三人选择同一部电影的概率.24. 如图,已知 , 点D , E分别在上,且满足 , . (1)、用直尺和圆规确定点D , E;(保留作图痕迹,不写作法)(2)、连接与交于点F . 若则的长为 .25. 如图,在中, , D是上一点,经过点A , C , D交于点E . 过点D作 , 分别交于点G , 于点F .
(1)、用直尺和圆规确定点D , E;(保留作图痕迹,不写作法)(2)、连接与交于点F . 若则的长为 .25. 如图,在中, , D是上一点,经过点A , C , D交于点E . 过点D作 , 分别交于点G , 于点F . (1)、求证;(2)、若 , 求的长.26. 中, , 于D , 于E , 交于F
(1)、求证;(2)、若 , 求的长.26. 中, , 于D , 于E , 交于F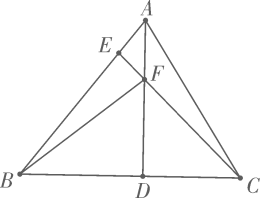 (1)、求证:;(2)、求(用含m的代数式表示);(3)、当时,求的最大值.27. 已知抛物线的解析式y=ax2+bx+3与x轴交于A、B两点,点B的坐标为(﹣1,0)抛物线与y轴正半轴交于点C,△ABC面积为6.
(1)、求证:;(2)、求(用含m的代数式表示);(3)、当时,求的最大值.27. 已知抛物线的解析式y=ax2+bx+3与x轴交于A、B两点,点B的坐标为(﹣1,0)抛物线与y轴正半轴交于点C,△ABC面积为6. (1)、如图1,求此抛物线的解析式;(2)、P为第一象限抛物线上一动点,过P作PG⊥AC,垂足为点G,设点P的横坐标为t,线段PG的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;(3)、如图2,在(2)的条件下,过点B作CP的平行线交y轴上一点F,连接AF,在BF的延长线上取点E,连接PE,若PE=AF,∠AFE+∠BEP=180°,求点P的坐标.
(1)、如图1,求此抛物线的解析式;(2)、P为第一象限抛物线上一动点,过P作PG⊥AC,垂足为点G,设点P的横坐标为t,线段PG的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;(3)、如图2,在(2)的条件下,过点B作CP的平行线交y轴上一点F,连接AF,在BF的延长线上取点E,连接PE,若PE=AF,∠AFE+∠BEP=180°,求点P的坐标.