江苏省苏州市吴中、吴江、相城区2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 下列四个实数中最大的是( )A、-2 B、 C、-1 D、2. 苏州围绕打造“处处皆景、城在园中”的“公园城市”目标,扎实推进民生实事项目口袋公园建设.2022年全年苏州各级园林绿化部门共投入资金145000000元进行新建、改建口袋公园,为市民打造更多家门口的幸福.145000000用科学记数法可以表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,在中, , , 按以下步骤作图:第一步,一点为圆心,适当的长为半径作弧,分别交 , 于、两点;第二步,分别以点、为圆心,大于的长为半径作弧,两弧相交于点;第三步,作射线 , 交于点 . 则的长为( )
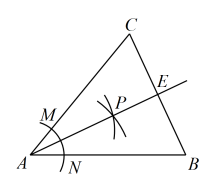 A、 B、8 C、 D、105. 为激励青少年爱读书、读好书、善读书,某校积极开展全员阅读活动.小吴为了了解本班同学一月的课外阅读量,随机选取班上部分同学进行调查,并将调查结果绘制成折线统计图(如图)下列说法中,正确的是( )
A、 B、8 C、 D、105. 为激励青少年爱读书、读好书、善读书,某校积极开展全员阅读活动.小吴为了了解本班同学一月的课外阅读量,随机选取班上部分同学进行调查,并将调查结果绘制成折线统计图(如图)下列说法中,正确的是( )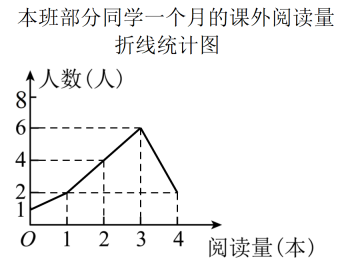 A、随机选取了14名同学 B、中位数是2本 C、众数是4本 D、平均数是2.4本6. 如图,正方形内接于 , 现有一小球可在内自由滚动,则小球停留在阴影部分内(各图形的边界忽略不计)的概率是( )
A、随机选取了14名同学 B、中位数是2本 C、众数是4本 D、平均数是2.4本6. 如图,正方形内接于 , 现有一小球可在内自由滚动,则小球停留在阴影部分内(各图形的边界忽略不计)的概率是( )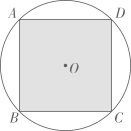 A、 B、 C、 D、7. 定义:两个不相交的函数图象在平行于轴方向上的最短距离称为这两个函数的“完美距离”.抛物线与直线的“完美距离”为( )A、 B、3 C、 D、8. 如图1,点为矩形中边的中点,点从点出发,沿以的速度运动到点 , 图2是点运动时,的面积随时间变化的函数图象,则的值为( )
A、 B、 C、 D、7. 定义:两个不相交的函数图象在平行于轴方向上的最短距离称为这两个函数的“完美距离”.抛物线与直线的“完美距离”为( )A、 B、3 C、 D、8. 如图1,点为矩形中边的中点,点从点出发,沿以的速度运动到点 , 图2是点运动时,的面积随时间变化的函数图象,则的值为( )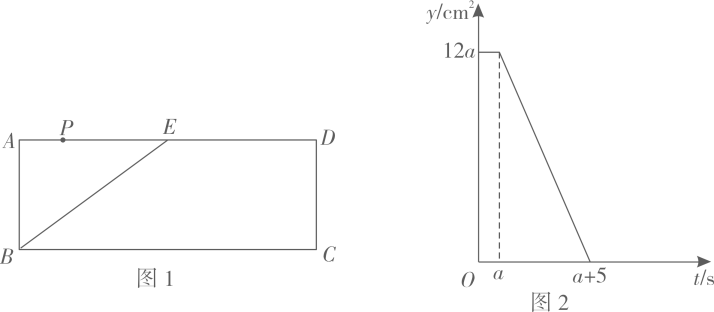 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
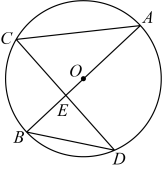
9. 计算: .10. 要使代数式 有意义,则 x 的取值范围是 .11. 若 ,则 = .12. 如图,是的直径,弦交于点 , , 连接 . 若 , , 则 .
 13. 已知圆锥底面圆直径为 , 母线长为 , 该圆锥侧面展开图扇形的圆心角度数为 .14. 关于的一元二次方程有一个大于的非正数根,那么实数的取值范围是 .15. 如图,直线与轴,轴分别交于点 , , 已知点坐标为 , 点是线段(不与点A , 重合)上一点,连接线段 , . 若 , 则点坐标为 .
13. 已知圆锥底面圆直径为 , 母线长为 , 该圆锥侧面展开图扇形的圆心角度数为 .14. 关于的一元二次方程有一个大于的非正数根,那么实数的取值范围是 .15. 如图,直线与轴,轴分别交于点 , , 已知点坐标为 , 点是线段(不与点A , 重合)上一点,连接线段 , . 若 , 则点坐标为 .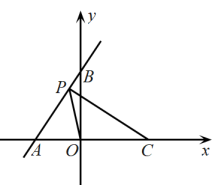 16. 如图,在中, , , 以为边在下方作 , 连接 , 已知 , , 则的最大值为 .
16. 如图,在中, , , 以为边在下方作 , 连接 , 已知 , , 则的最大值为 .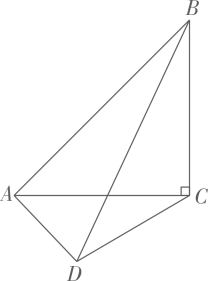
三、解答题
-
17. 计算: .18. 解方程 .19. 已知 , 求的值.20. 为缓减校园周边道路的交通压力,及时调整学生上学时间,某校需要了解本校学生的上学方式,学生可以从“:步行,:骑自行车,:乘坐公共交通,:家用汽车接送,:其他方式”.五个选项中进行选择.(1)、学生甲随机选择“:乘坐公共交通”方式的概率为 .(2)、若两名学生分别从 , , , , 五种上学方式中随机选择一种,求两名学生一人选择“:步行”,另一人选择“:乘坐公共交通”的概率(请用画树状图或列表等方法说明理由).21. 如图, , 交于点 , , .
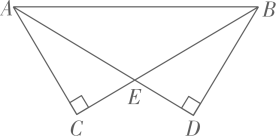 (1)、求证:;(2)、若 , 求的度数.22. 适当的劳动对青少年的成长和发展具有十分重要的意义.为了解八年级学生每周家务劳动的总时长,某校数学社团成员采用随机抽样的方法,抽取了八年级部分学生,对他们一周内家务劳动总时间(单位:小时)进行了调查,并将数据整理后得到下列不完整的统计图表:
(1)、求证:;(2)、若 , 求的度数.22. 适当的劳动对青少年的成长和发展具有十分重要的意义.为了解八年级学生每周家务劳动的总时长,某校数学社团成员采用随机抽样的方法,抽取了八年级部分学生,对他们一周内家务劳动总时间(单位:小时)进行了调查,并将数据整理后得到下列不完整的统计图表:组别
家务劳动总时间分组
频数
5
7
10
19
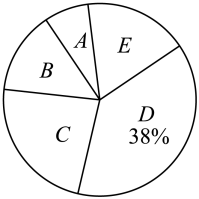
请根据图表信息回答下列问题:
(1)、频数分布表中,(2)、扇形统计图中,组所在扇形的圆心角的度数是 .(3)、请估计该校650名八年级学生中一周内家务劳动总时间不少于8小时的人数.23. 如图,反比例函数的图像经过边长为4的正方形的顶点A , 与正方形的边交于点 , 且 .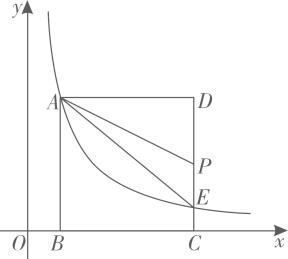 (1)、求的值;(2)、若点是正方形边上不与点重合的点,连接 , , 当的面积为时,求点的坐标.24. 为迎接五一假期的到来,某景区一商户准备了两种当地特产礼盒,按成本价1件A种礼盒和2件种礼盒共需320元,2件A种礼盒和3件种礼盒共需540元.(1)、求A、两种礼盒每件的成本价分别是多少元?(2)、若种礼盒的售价为每件150元,种礼盒的售价为每件120元.商户原计划在五一当天将现有的、两种礼盒共56件按售价全部售出,但在实际销售过程中56件商品没有全部售完,两种礼盒的实际销售利润总和为1320元.五一当天商户最多卖出种礼盒多少件?25. 如图,已知 , 是的两条直径,直径平分 , 的一边与和直径分别交于点 , , 连接 , 且 .
(1)、求的值;(2)、若点是正方形边上不与点重合的点,连接 , , 当的面积为时,求点的坐标.24. 为迎接五一假期的到来,某景区一商户准备了两种当地特产礼盒,按成本价1件A种礼盒和2件种礼盒共需320元,2件A种礼盒和3件种礼盒共需540元.(1)、求A、两种礼盒每件的成本价分别是多少元?(2)、若种礼盒的售价为每件150元,种礼盒的售价为每件120元.商户原计划在五一当天将现有的、两种礼盒共56件按售价全部售出,但在实际销售过程中56件商品没有全部售完,两种礼盒的实际销售利润总和为1320元.五一当天商户最多卖出种礼盒多少件?25. 如图,已知 , 是的两条直径,直径平分 , 的一边与和直径分别交于点 , , 连接 , 且 .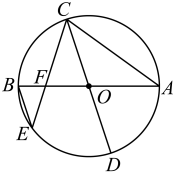 (1)、证明:;(2)、若 , 求的长.26. 如图,拋物线(a是常数且)与轴交于点 , 两点(点位于点右侧),与轴交于点 , 点为拋物线的顶点,且点的坐标为 , 连接 , , .
(1)、证明:;(2)、若 , 求的长.26. 如图,拋物线(a是常数且)与轴交于点 , 两点(点位于点右侧),与轴交于点 , 点为拋物线的顶点,且点的坐标为 , 连接 , , .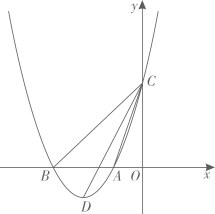 (1)、求该抛物线的表达式;(2)、若点为抛物线上的点,连接 , 当时,求点的坐标;(3)、若在轴上总存在一点 , 且点的横坐标为 , 当时,直接写出的取值范围.27.(1)、【问题探究】
(1)、求该抛物线的表达式;(2)、若点为抛物线上的点,连接 , 当时,求点的坐标;(3)、若在轴上总存在一点 , 且点的横坐标为 , 当时,直接写出的取值范围.27.(1)、【问题探究】课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形中,点 , 分别是边 , 上的点,连接 , , 且于点 , 若 , , 求的值.
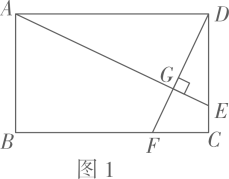
请你帮助同学们解决上述问题,并说明理由.
(2)、【初步运用】如图2,在中, , , 点为的中点,连接 , 过点作于点 , 交于点 , 求的值.
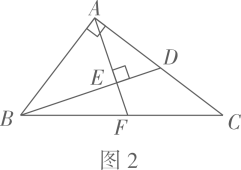 (3)、【灵活运用】
(3)、【灵活运用】如图3,在四边形中, , , , , 点 , 分别在边 , 上,且 , 垂足为 , 则 .
