黑龙江省齐齐哈尔市龙江县2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、2023 C、 D、2. 下列图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是两圆柱形连通容器,向甲容器匀速注水,则下面可以近似地刻画甲容器的水面高度随时间分的变化情况的是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是两圆柱形连通容器,向甲容器匀速注水,则下面可以近似地刻画甲容器的水面高度随时间分的变化情况的是( )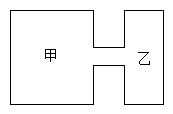 A、
A、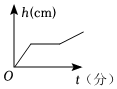 B、
B、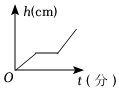 C、
C、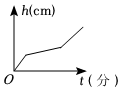 D、
D、 5. 一个由长方体截去一部分后得到的几何体如图水平放置,其俯视图是( )
5. 一个由长方体截去一部分后得到的几何体如图水平放置,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,一个三角板的两个直角边经过矩形相邻的两个顶点,若 , 则的度数为( )
6. 如图,一个三角板的两个直角边经过矩形相邻的两个顶点,若 , 则的度数为( ) A、 B、 C、 D、7. 如图,点在轴的正半轴上,点在第一象限, , 反比例函数的图像经过点 , 反比例函数的图像经过点 . 若 , 则的值为( )
A、 B、 C、 D、7. 如图,点在轴的正半轴上,点在第一象限, , 反比例函数的图像经过点 , 反比例函数的图像经过点 . 若 , 则的值为( ) A、2 B、3 C、4 D、58. 为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率是( )A、 B、 C、 D、9. 国家“双减”政策实施后,某校开展了丰富多彩的社团活动.某班同学报名参加书法和围棋两个社团,班长为参加社团的同学去商场购买毛笔和围棋(两种都购买)共花费360元.其中毛笔每支15元,围棋每副20元,共有多少种购买方案?( )A、5 B、6 C、7 D、810. 如图,已知二次函数(为常数且)图象的顶点为 , 且经过点 . 有以下结论:①;②;③;④时,随的增大而减小;⑤对于任意实数 , 总有 . 其中结论正确的个数有( )
A、2 B、3 C、4 D、58. 为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率是( )A、 B、 C、 D、9. 国家“双减”政策实施后,某校开展了丰富多彩的社团活动.某班同学报名参加书法和围棋两个社团,班长为参加社团的同学去商场购买毛笔和围棋(两种都购买)共花费360元.其中毛笔每支15元,围棋每副20元,共有多少种购买方案?( )A、5 B、6 C、7 D、810. 如图,已知二次函数(为常数且)图象的顶点为 , 且经过点 . 有以下结论:①;②;③;④时,随的增大而减小;⑤对于任意实数 , 总有 . 其中结论正确的个数有( )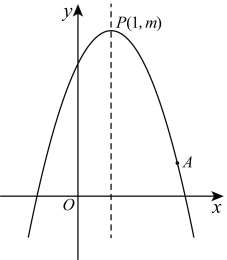 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 商业航天在近几年得到快速成长并初具规模,2022年中国商业航天的市场规模突破1.5万亿元.将1.5万亿用科学记数法表示为 .12. 在函数y=中,自变量x的取值范围是 .
13. 如图,已知 , , 请你添加一个条件 , 使.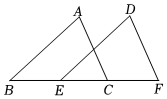 14. 已知圆锥的底面圆的半径为6,高为8,则它的侧面展开图的面积是 .15. 若关于的分式方程有正整数解,则整数 .16. 已知菱形的边长为4, , 点在边上且 , 是菱形边上的一点,若是以为腰的等腰三角形,则的面积为 .17. 平面直角坐标系中,矩形的位置如图,点 , . 连接 , 以为一边作矩形且;连接 , 以为一边作矩形且;连接 , 以为一边作矩形且……按这样的规律进行下去,则点的坐标为 .
14. 已知圆锥的底面圆的半径为6,高为8,则它的侧面展开图的面积是 .15. 若关于的分式方程有正整数解,则整数 .16. 已知菱形的边长为4, , 点在边上且 , 是菱形边上的一点,若是以为腰的等腰三角形,则的面积为 .17. 平面直角坐标系中,矩形的位置如图,点 , . 连接 , 以为一边作矩形且;连接 , 以为一边作矩形且;连接 , 以为一边作矩形且……按这样的规律进行下去,则点的坐标为 .
三、解答题
-
18.(1)、计算:;(2)、分解因式: .19. 解方程: .20. 某市教育局为了解“双减”政策落实情况,随机抽取几所学校部分初中生进行调查,统计他们平均每天完成作业的时间,并根据调查结果绘制如下不完整的统计图:
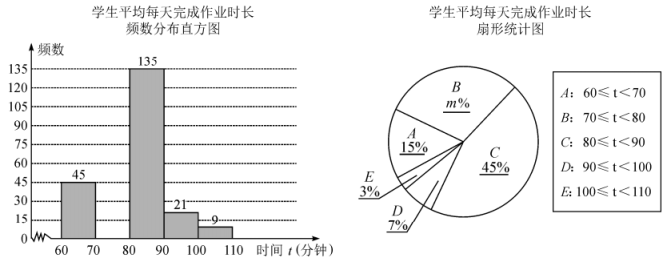
请根据图表中提供的信息,解答下面的问题:
(1)、在调查活动中,教育局采取的调查方式是(填写“普查”或“抽样调查”);(2)、教育局抽取的初中生有人,扇形统计图中m的值是;(3)、已知平均每天完成作业时长在“”分钟的9名初中生中有5名男生和4名女生,若从这9名学生中随机抽取一名进行访谈,且每一名学生被抽到的可能性相同,则恰好抽到男生的概率是;(4)、若该市共有初中生10000名,则平均每天完成作业时长在“”分钟的初中生约有人.21. 如图,是的直径,点在圆上,点在圆外,点和点在直径的同侧,与相交于点 .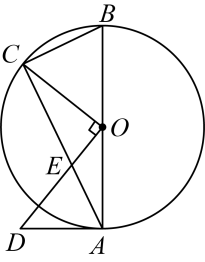 (1)、求证:是的切线;(2)、若的半径为4, , 求的面积.22. 在救灾期间,甲市派一辆货车将蔬菜运往的乙市,途中因故障停留一段时间,之后降速行驶.一辆轿车沿同一条公路从乙市前往甲市,到达甲市停留半小时后,原路原速返回.如图是两车距各自出发地的路程(单位:)与货车出发的时间(单位:)之间的函数图象,结合图象回答下列问题:
(1)、求证:是的切线;(2)、若的半径为4, , 求的面积.22. 在救灾期间,甲市派一辆货车将蔬菜运往的乙市,途中因故障停留一段时间,之后降速行驶.一辆轿车沿同一条公路从乙市前往甲市,到达甲市停留半小时后,原路原速返回.如图是两车距各自出发地的路程(单位:)与货车出发的时间(单位:)之间的函数图象,结合图象回答下列问题: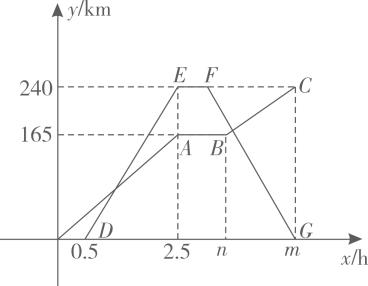 (1)、图中的值是 , 的值是;轿车的速度是;(2)、求货车从甲市前往乙市的过程中,货车距出发地的路程(单位:)与出发时间(单位:h)之间的函数关系式;(3)、直接写出轿车出发多长时间与货车相距 .23. 折纸是一项有趣的活动,有的同学玩过折纸,可能折过小动物、飞机、小船等.在折纸过程中,不仅可以得到一些美丽的图形,而且其中还蕴含着丰富的数学知识.
(1)、图中的值是 , 的值是;轿车的速度是;(2)、求货车从甲市前往乙市的过程中,货车距出发地的路程(单位:)与出发时间(单位:h)之间的函数关系式;(3)、直接写出轿车出发多长时间与货车相距 .23. 折纸是一项有趣的活动,有的同学玩过折纸,可能折过小动物、飞机、小船等.在折纸过程中,不仅可以得到一些美丽的图形,而且其中还蕴含着丰富的数学知识.如图①,菱形纸片中, .
 (1)、活动一:
(1)、活动一:如图②,折叠菱形纸片 , 使点落在点处,则折痕的长为;菱形纸片的面积是;
(2)、活动二:如图③,分别是菱形纸片各边的中点,分别沿着折叠并展开.猜想四边形是什么特殊四边形,并证明你的猜想;
(3)、活动三:如图④,先将菱形纸片沿折叠再展开,点分别在边上且 , 再分别沿着折叠再展开,若四边形是正方形,则;
(4)、活动四:如图⑤,折叠菱形纸片 , 使点落在边的中点处,则折痕的长为 .
24. 综合与探究如图,在平面直角坐标系中,抛物线与轴交于点 , 与轴交于点 , , 为拋物线的顶点,连接 .
 (1)、求抛物线的解析式;(2)、顶点的坐标为;已知点在抛物线上,当时,则的取值范围为;(3)、 是线段上的一个动点,连接 , 当线段最短时,请求出点的坐标;(4)、若是对称轴上的动点,在坐标平面内是否存在点 , 使以为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、顶点的坐标为;已知点在抛物线上,当时,则的取值范围为;(3)、 是线段上的一个动点,连接 , 当线段最短时,请求出点的坐标;(4)、若是对称轴上的动点,在坐标平面内是否存在点 , 使以为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.