黑龙江省龙东地区2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 下列计算中,正确的是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
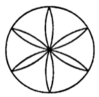 B、
B、 C、
C、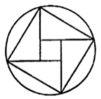 D、
D、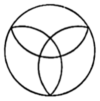 3. 已知一组数据2,a , 4,5的众数为5,则这组数据的平均数为( )A、6 B、5 C、4 D、34. 如图是由一些完全相同的小立方块搭成的几何体从左面、上面看到的形状图.搭成这个几何体所用的小立方块的个数至少是( )
3. 已知一组数据2,a , 4,5的众数为5,则这组数据的平均数为( )A、6 B、5 C、4 D、34. 如图是由一些完全相同的小立方块搭成的几何体从左面、上面看到的形状图.搭成这个几何体所用的小立方块的个数至少是( ) A、3个 B、4个 C、5个 D、6个5. 某种品牌运动服经过两次降价,每件零售价由元降为元.已知两次降价的百分率都是 , 则x的值是( )A、 B、25 C、 D、206. 已知关于x的分式方程的解为负数,则k的取值范围是( )A、 B、且 C、 D、且7. 装乒乓球的盒子有两种,大盒装6个,小盒装4个,若将50个乒乓球都装进盒子且把每个盒子都装满,那么不同的装球方法有( )A、3种 B、4种 C、5种 D、6种8. 如图,A是反比例函数图象上一点,过点A作轴于点D , 且D为线段的中点.若C为x轴上任意一点,且的面积为11,则k的值为( )
A、3个 B、4个 C、5个 D、6个5. 某种品牌运动服经过两次降价,每件零售价由元降为元.已知两次降价的百分率都是 , 则x的值是( )A、 B、25 C、 D、206. 已知关于x的分式方程的解为负数,则k的取值范围是( )A、 B、且 C、 D、且7. 装乒乓球的盒子有两种,大盒装6个,小盒装4个,若将50个乒乓球都装进盒子且把每个盒子都装满,那么不同的装球方法有( )A、3种 B、4种 C、5种 D、6种8. 如图,A是反比例函数图象上一点,过点A作轴于点D , 且D为线段的中点.若C为x轴上任意一点,且的面积为11,则k的值为( ) A、 B、 C、11 D、9. 如图,在四边形中, , , 作于点E , , 连接 , , 则的长为( )
A、 B、 C、11 D、9. 如图,在四边形中, , , 作于点E , , 连接 , , 则的长为( ) A、10 B、8 C、6 D、410. 如图,在正方形中,点E在边上,点H在边上, , 交于点F , 交于点G , 连接 . 下列结论:①;②;③;④当E是的中点时,;⑤当时, . 其中正确结论的序号是( )
A、10 B、8 C、6 D、410. 如图,在正方形中,点E在边上,点H在边上, , 交于点F , 交于点G , 连接 . 下列结论:①;②;③;④当E是的中点时,;⑤当时, . 其中正确结论的序号是( ) A、①②③④ B、①②③⑤ C、①③④⑤ D、②①⑤
A、①②③④ B、①②③⑤ C、①③④⑤ D、②①⑤二、填空题
-
11. 据统计,我国每年浪费粮食约是35000000吨,将35000000用科学记数法表示为 .12. 函数的自变量x的取值范围是 .13. 如图,与相交于点A , 与相交于点B , , 垂足为P , 添加一个条件 , 使≌(填一个即可).
 14. 随机掷一枚均匀的正方体骰子,骰子停止后朝上的点数小于3的概率是 .15. 若关于x的不等式组的解集是 , 则a的取值范围是 .16. 已知是半径为2cm的圆的内接三角形, , 则 .17. 已知圆锥的母线长为 高为 则该圆锥侧面展开图的圆心角是 .18. 如图,在中, , , 交于点D , P为线段上的动点,则的最小值为 .
14. 随机掷一枚均匀的正方体骰子,骰子停止后朝上的点数小于3的概率是 .15. 若关于x的不等式组的解集是 , 则a的取值范围是 .16. 已知是半径为2cm的圆的内接三角形, , 则 .17. 已知圆锥的母线长为 高为 则该圆锥侧面展开图的圆心角是 .18. 如图,在中, , , 交于点D , P为线段上的动点,则的最小值为 .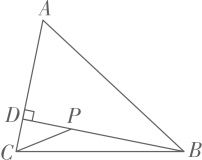 19. 在矩形中, , , M是直线上的一点,将沿折叠,得到 , 连接 , 若 , 则的长为 .20. 如图,射线与x轴所夹的锐角为 , 的长为1, , , , …,均为等边三角形,点 , , , …,在x轴的正半轴上依次排列,点 , , , …,在射线上依次排列,那么点的坐标为 .
19. 在矩形中, , , M是直线上的一点,将沿折叠,得到 , 连接 , 若 , 则的长为 .20. 如图,射线与x轴所夹的锐角为 , 的长为1, , , , …,均为等边三角形,点 , , , …,在x轴的正半轴上依次排列,点 , , , …,在射线上依次排列,那么点的坐标为 .
三、解答题
-
21. 先化简,再求值: , 其中 .22. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
 (1)、若经过平移后得到 , 已知点的坐标为 , 画出 , 并写出点的坐标;(2)、将绕着点O按逆时针方向旋转得到 , 画出 , 并写出点的坐标;(3)、求出(2)中点A旋转到点所经过的路径长.23. 已知抛物线经过点和点 , 与y轴交于点C , P为第二象限内抛物线上一点.
(1)、若经过平移后得到 , 已知点的坐标为 , 画出 , 并写出点的坐标;(2)、将绕着点O按逆时针方向旋转得到 , 画出 , 并写出点的坐标;(3)、求出(2)中点A旋转到点所经过的路径长.23. 已知抛物线经过点和点 , 与y轴交于点C , P为第二象限内抛物线上一点.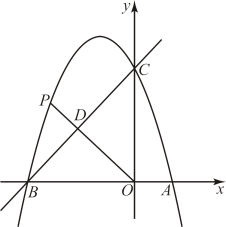 (1)、求抛物线的解析式;(2)、如图,连接交直线于点D , 当时,直接写出点P的横坐标.24. 为了解七年级同学最喜欢看哪一类课外书,某校随机抽取本校七年级部分同学进行问卷调查(每人必选且只选择一种最喜欢的书籍类型).如图是根据调查结果绘制的两幅不完整的统计图.请根据统计图的信息,解答下列问题:
(1)、求抛物线的解析式;(2)、如图,连接交直线于点D , 当时,直接写出点P的横坐标.24. 为了解七年级同学最喜欢看哪一类课外书,某校随机抽取本校七年级部分同学进行问卷调查(每人必选且只选择一种最喜欢的书籍类型).如图是根据调查结果绘制的两幅不完整的统计图.请根据统计图的信息,解答下列问题: (1)、一共有多少名学生参与了本次问卷调查?(2)、补全条形统计图;(3)、扇形统计图中“其他”所在扇形的圆心角度数为;(4)、若该校七年级有1500名学生,请你估计喜欢“科普常识”的学生人数.25. 小张骑摩托车从A地去B地,小王驾车从B地去A地再返回B地.两人同时出发,小张骑摩托车的速度为 , 小王去A地用了 , 返回时速度有所提高,小张、小王两人离A地的路程y(单位:km)与小张出发的时间x(单位:h)之间的函数关系如图所示.
(1)、一共有多少名学生参与了本次问卷调查?(2)、补全条形统计图;(3)、扇形统计图中“其他”所在扇形的圆心角度数为;(4)、若该校七年级有1500名学生,请你估计喜欢“科普常识”的学生人数.25. 小张骑摩托车从A地去B地,小王驾车从B地去A地再返回B地.两人同时出发,小张骑摩托车的速度为 , 小王去A地用了 , 返回时速度有所提高,小张、小王两人离A地的路程y(单位:km)与小张出发的时间x(单位:h)之间的函数关系如图所示. (1)、A , B两地之间的路程为;(2)、求出小王返回追上小张时,他们离B地的距离;(3)、直接写出小王从A地返回B地的过程中,与小张相距12千米时的行驶时间.26. 已知为等边三角形,点D在边上,点F在射线上,以为一边作等边三角形 , 连接 .
(1)、A , B两地之间的路程为;(2)、求出小王返回追上小张时,他们离B地的距离;(3)、直接写出小王从A地返回B地的过程中,与小张相距12千米时的行驶时间.26. 已知为等边三角形,点D在边上,点F在射线上,以为一边作等边三角形 , 连接 . (1)、当点F与点A重合时,如图①,线段 , , 之间的数量关系是;(2)、点F在边上时,如图②;当点F在边的延长线上时,如图③,猜想线段 , , 之间存在怎样的数量关系?写出你的猜想,并对图③的猜想给予证明.27. 某手机经销商计划同时购进甲乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需要资金6000元;若购进3部甲型号手机和2部乙型号手机,共需要资金4600元.(1)、求甲、乙型号手机每部进价各为多少元;(2)、该店预计用不少于1.78万元且不多于1.92万元的资金购进这两种型号手机共20部,请问有多少种进货方案?(3)、若甲型号手机的售价为1500元,乙型号手机的售价为1450元,为了促销,公司决定每售出一台乙型号手机.返还顾客现金a元,甲型号手机售价不变,要使(2)中购进的手机全部售完,每种方案获利相同,求a的值.28. 如图,矩形的顶点A , C分别在x轴和y轴上, , 的长是一元二次方程的两个实数根,点P从点C出发,以每秒个单位长度的速度向终点O运动,同时点Q从点C出发,以每秒1个单位长度的速度向终点B运动,将沿直线折叠得到 , 设与矩形重合部分的面积为S , 运动时间为t秒.
(1)、当点F与点A重合时,如图①,线段 , , 之间的数量关系是;(2)、点F在边上时,如图②;当点F在边的延长线上时,如图③,猜想线段 , , 之间存在怎样的数量关系?写出你的猜想,并对图③的猜想给予证明.27. 某手机经销商计划同时购进甲乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需要资金6000元;若购进3部甲型号手机和2部乙型号手机,共需要资金4600元.(1)、求甲、乙型号手机每部进价各为多少元;(2)、该店预计用不少于1.78万元且不多于1.92万元的资金购进这两种型号手机共20部,请问有多少种进货方案?(3)、若甲型号手机的售价为1500元,乙型号手机的售价为1450元,为了促销,公司决定每售出一台乙型号手机.返还顾客现金a元,甲型号手机售价不变,要使(2)中购进的手机全部售完,每种方案获利相同,求a的值.28. 如图,矩形的顶点A , C分别在x轴和y轴上, , 的长是一元二次方程的两个实数根,点P从点C出发,以每秒个单位长度的速度向终点O运动,同时点Q从点C出发,以每秒1个单位长度的速度向终点B运动,将沿直线折叠得到 , 设与矩形重合部分的面积为S , 运动时间为t秒. (1)、求点B的坐标;(2)、求S与t的函数关系式,并写出自变量的取值范围;(3)、当点D落在上时,点N在x轴上,直线上是否存在点M , 使以D , Q , M , N为顶点的四边形是平行四边形?若存在,直接与出点M的坐标;若不存在,请说明理由.
(1)、求点B的坐标;(2)、求S与t的函数关系式,并写出自变量的取值范围;(3)、当点D落在上时,点N在x轴上,直线上是否存在点M , 使以D , Q , M , N为顶点的四边形是平行四边形?若存在,直接与出点M的坐标;若不存在,请说明理由.