黑龙江省大庆市龙凤区2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 2022年我国的进出口总额超过了6万亿美元,实际使用外资亿美元,规模再创历史新高.将189130000000用科学记数法表示应为( )A、 B、 C、 D、3. 剪纸是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上透空的感觉和艺术享受.春节期间,剪纸爱好者发起“百牛迎新春”剪纸创作活动.下列作品中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是 ( )A、 B、 C、 D、5. 分式的值是零,则的值为( )A、5 B、 C、 D、26. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 某博物馆拟招聘一名优秀志愿讲解员,其中某位志愿者笔试、试讲、面试三轮测试得分分别为90分、94分、92分,综合成绩中笔试占 , 试讲占 , 面试占 , 则该名志愿者的综合成绩为( )A、94分 B、92.4分 C、92分 D、90.5分8. 如图是由三个大小不同的正方体拼成的几何体,其主视图、左视图、俯视图的面积分别为 , , , 则 , , 的大小关系是( )
4. 下列运算正确的是 ( )A、 B、 C、 D、5. 分式的值是零,则的值为( )A、5 B、 C、 D、26. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 某博物馆拟招聘一名优秀志愿讲解员,其中某位志愿者笔试、试讲、面试三轮测试得分分别为90分、94分、92分,综合成绩中笔试占 , 试讲占 , 面试占 , 则该名志愿者的综合成绩为( )A、94分 B、92.4分 C、92分 D、90.5分8. 如图是由三个大小不同的正方体拼成的几何体,其主视图、左视图、俯视图的面积分别为 , , , 则 , , 的大小关系是( )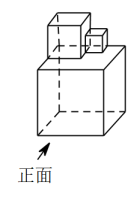 A、 B、 C、 D、9. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( )
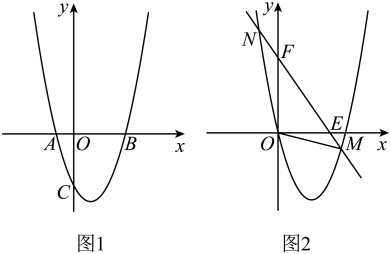
A、 B、 C、 D、9. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( ) A、60° B、75° C、90° D、105°10. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图象如图所示,给出以下判断:①且;②;③;④ . 其中错误的选项是( )
A、60° B、75° C、90° D、105°10. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图象如图所示,给出以下判断:①且;②;③;④ . 其中错误的选项是( ) A、①③ B、①③④ C、②④ D、②③④
A、①③ B、①③④ C、②④ D、②③④二、填空题
-
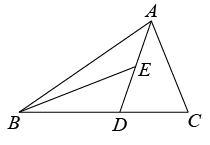
11. 如果单项式与是同类项,那么 .12. 若 , , 则 .13. 关于x的方程有增根,则m的值是 .14. 如图,中,AD是的角平分线,BE是边AD上的中线,若的面积是24, , , 则的面积是 .
 15. 若关于x的一元一次不等式有且只有5个正整数解,则n的取值范围是 .16. 如图,在平面直角坐标系中, , , 点 , , 在直线l上,点 , , , 在轴的正半轴上,若 , , , , 依次均为等腰直角三角形,直角顶点都在轴上,则第个等腰直角三角形顶点的横坐标为 .
15. 若关于x的一元一次不等式有且只有5个正整数解,则n的取值范围是 .16. 如图,在平面直角坐标系中, , , 点 , , 在直线l上,点 , , , 在轴的正半轴上,若 , , , , 依次均为等腰直角三角形,直角顶点都在轴上,则第个等腰直角三角形顶点的横坐标为 . 17. 如图,的顶点 , ),以点B为圆心,长为半径画弧,交于点E , 分别以点A , E为圆心,以大于的长为半径画弧,两弧在的内部相交于点F , 画射线交于点G , 则点G的坐标是 .
17. 如图,的顶点 , ),以点B为圆心,长为半径画弧,交于点E , 分别以点A , E为圆心,以大于的长为半径画弧,两弧在的内部相交于点F , 画射线交于点G , 则点G的坐标是 .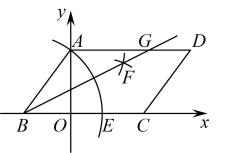 18. 如图,正方形的边长为2,G是对角线上一动点,于点E , 于点F , 连接 . 给出四种情况:①若G为上任意一点,则;②若 , 则;③若G为的中点,则四边形是正方形;④若 , 则 . 则其中正确的是 .
18. 如图,正方形的边长为2,G是对角线上一动点,于点E , 于点F , 连接 . 给出四种情况:①若G为上任意一点,则;②若 , 则;③若G为的中点,则四边形是正方形;④若 , 则 . 则其中正确的是 .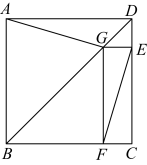
三、解答题
-
19. 计算: .20. 先化简 , 然后在范围内,选择一个合适的整数代入求值.21. 八年(1)班学生周末乘汽车到抗美援朝纪念馆参观,纪念馆距离学校60km.一部分学生乘慢车先行,出发后,另一部分学生乘快车前往,结果他们同时到达纪念馆.已知快车的速度是慢车速度的1.5倍,求慢车的速度.22. “格物致知,叩问苍穹”,年中国航天日活动于4月日在安徽合肥隆重举行.受活动影响,某校航模社团制作了一种固定翼飞机的机翼模型,形状如图所示,经测量 , , , , , 求边的长.(参考数据: , , ; , , )
 23. 池州某中学在落实“双减”的背景下,决定在课后延时服务中组织学生开展社团活动,现准备开设手工、摄影、航模、编程四门校本课程,规定每名学生必须且只能选修一门校本课程,学校对七年级学生选修校本课程的情况进行了抽样调查,根据调查结果绘制了下面两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题.
23. 池州某中学在落实“双减”的背景下,决定在课后延时服务中组织学生开展社团活动,现准备开设手工、摄影、航模、编程四门校本课程,规定每名学生必须且只能选修一门校本课程,学校对七年级学生选修校本课程的情况进行了抽样调查,根据调查结果绘制了下面两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题. (1)、本次调查,一共调查了名学生;(2)、补全条形统计图和扇形统计图;(3)、若本次调查中选择“航模”课程中的女生占20%,则在全校2800名学生中,请你估计约有多少名女生会选择“航模”课程;(4)、手工学生小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端、、三个绳头中随机选两个打一个结,求这三根绳子连接成一根长绳的概率.
(1)、本次调查,一共调查了名学生;(2)、补全条形统计图和扇形统计图;(3)、若本次调查中选择“航模”课程中的女生占20%,则在全校2800名学生中,请你估计约有多少名女生会选择“航模”课程;(4)、手工学生小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端、、三个绳头中随机选两个打一个结,求这三根绳子连接成一根长绳的概率. 24. 已知:如图,是的角平分线,交于点 , 交于点 .
24. 已知:如图,是的角平分线,交于点 , 交于点 .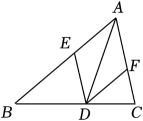 (1)、求证:四边形是菱形;(2)、若 , , 试求四边形的面积.25. 如图,一次函数的图象与y轴交于点A , 与反比例函数的图象交于点和点 , 连接 .
(1)、求证:四边形是菱形;(2)、若 , , 试求四边形的面积.25. 如图,一次函数的图象与y轴交于点A , 与反比例函数的图象交于点和点 , 连接 .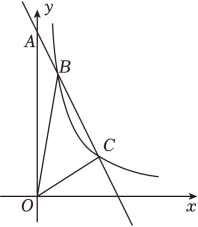 (1)、求的值;(2)、求的面积.26. 某超市购进了一种商品,进价为每件8元,销售过程中发现,该商品每天的销售量(件)与每件售价(元)之间存在某种函数关系(其中 , 且为整数),且当时,;当时,;当时,;…,设超市销售这种消毒用品每天获利为(元).(1)、请判断与符合哪种函数关系,并求与的函数表达式;(2)、若该商店销售这种商品每天获润480元,则每件商品的售价为多少元;(3)、当每件商品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
(1)、求的值;(2)、求的面积.26. 某超市购进了一种商品,进价为每件8元,销售过程中发现,该商品每天的销售量(件)与每件售价(元)之间存在某种函数关系(其中 , 且为整数),且当时,;当时,;当时,;…,设超市销售这种消毒用品每天获利为(元).(1)、请判断与符合哪种函数关系,并求与的函数表达式;(2)、若该商店销售这种商品每天获润480元,则每件商品的售价为多少元;(3)、当每件商品的售价为多少元时,每天的销售利润最大?最大利润是多少元?