广西壮族自治区南宁市2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 2的相反数是( )A、 B、2 C、 D、2. 2023年3月5日十四届全国人大一次会议审议通过的政府工作报告中指出,过去的一年全国粮食产量1370000000000斤,数据1370000000000用科学记数法表示应为( )A、 B、 C、 D、3. 如图所示的几何体是由5个完全相同的小正方体搭成的,它的左视图是( )
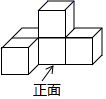 A、
A、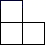 B、
B、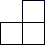 C、
C、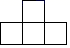 D、
D、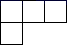 4. 下列计算中,正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、调查南宁邕江的水质情况,适合全面调查 B、调查一架“歼20”战斗机各零部件的质量,适合抽样调查 C、甲、乙两人跳远成绩的方差分别为 , , 说明甲的跳远成绩比乙稳定 D、“经过有交通信号灯的路口,遇到红灯”是随机事件6. 若不等式的解集为x<-2,则以下数轴表示中正确的是( )A、
4. 下列计算中,正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、调查南宁邕江的水质情况,适合全面调查 B、调查一架“歼20”战斗机各零部件的质量,适合抽样调查 C、甲、乙两人跳远成绩的方差分别为 , , 说明甲的跳远成绩比乙稳定 D、“经过有交通信号灯的路口,遇到红灯”是随机事件6. 若不等式的解集为x<-2,则以下数轴表示中正确的是( )A、 B、
B、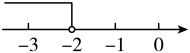 C、
C、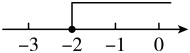 D、
D、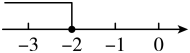 7. 一个口袋中有红球、白球共20个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有40次摸到白球.请你估计这个口袋中有( )个白球.A、12 B、8 C、6 D、48. 计算的结果是( )A、 B、 C、 D、9. 如图,圆规两脚 , 张开的角度 , , 则两脚张开的距离为( )
7. 一个口袋中有红球、白球共20个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有40次摸到白球.请你估计这个口袋中有( )个白球.A、12 B、8 C、6 D、48. 计算的结果是( )A、 B、 C、 D、9. 如图,圆规两脚 , 张开的角度 , , 则两脚张开的距离为( ) A、 B、 C、 D、10. 在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面( )尺.
A、 B、 C、 D、10. 在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面( )尺. A、4 B、3.6 C、4.5 D、4.5511. 小明在拼图时发现8个一样大小的长方形恰好拼成一个大的长方形,如图1所示.小红看见了,说:“我也来试一试.“结果小红七拼八凑,拼成如图2那样的正方形,但中间留下了一个洞,恰好是边长为的小正方形,则每个小长方形的长和宽分别为( )
A、4 B、3.6 C、4.5 D、4.5511. 小明在拼图时发现8个一样大小的长方形恰好拼成一个大的长方形,如图1所示.小红看见了,说:“我也来试一试.“结果小红七拼八凑,拼成如图2那样的正方形,但中间留下了一个洞,恰好是边长为的小正方形,则每个小长方形的长和宽分别为( ) A、 , B、 , C、 , D、 ,12. 如图,在平面直角坐标系中,点P在反比例函数的图象上,点A , B在x轴上,且 , 垂足为P , PA交y轴于点C , , 的面积是2.则k的值是( )
A、 , B、 , C、 , D、 ,12. 如图,在平面直角坐标系中,点P在反比例函数的图象上,点A , B在x轴上,且 , 垂足为P , PA交y轴于点C , , 的面积是2.则k的值是( )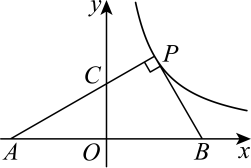 A、1 B、 C、 D、2
A、1 B、 C、 D、2二、填空题
-
13. 如果电梯上升8层记作层,那么下降2层记作层.14. 因式分解: .15. 如图,在中,弦 , 相交于点P . 若 , , 则度数为 .
 16. 某校为开展“永远跟党走、奋进新征程”主题党的二十大教育宣讲活动,学校从2名男老师和2名女老师中随机选取2名教师作为宣讲员,则恰好选中1名男老师和1名女老师的概率为 .17. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日迫及之.”意思是:现有良马每天行走240里,驽马每天行走150里,驽马先走12天,问良马几天可以追上驽马?两匹马行走路程S(里)与行走时间t(日)的函数关系如图所示,则图中交点P的坐标是 .
16. 某校为开展“永远跟党走、奋进新征程”主题党的二十大教育宣讲活动,学校从2名男老师和2名女老师中随机选取2名教师作为宣讲员,则恰好选中1名男老师和1名女老师的概率为 .17. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日迫及之.”意思是:现有良马每天行走240里,驽马每天行走150里,驽马先走12天,问良马几天可以追上驽马?两匹马行走路程S(里)与行走时间t(日)的函数关系如图所示,则图中交点P的坐标是 .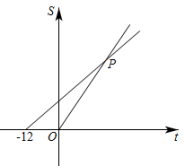 18. 如图,四边形为正方形纸片,E是边的中点,连接 , P是边上一点,将纸片沿着折叠,使点D落在上的F点处,则为 .
18. 如图,四边形为正方形纸片,E是边的中点,连接 , P是边上一点,将纸片沿着折叠,使点D落在上的F点处,则为 .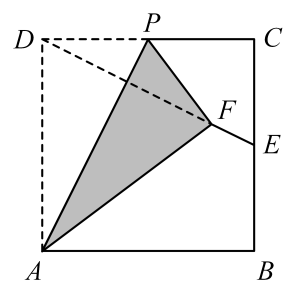
三、解答题
-
19. 计算: .20. 解分式方程: .21. 如图,在的正方形网格中,每个小正方形的边长为1,的顶点都是网格线的交点.
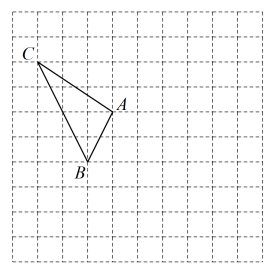
⑴在如图所示的网格平面内画出以A为坐标原点的平面直角坐标系 , 并写出A , B , C三点坐标;
⑵在平面直角坐标系中画出关于y轴对称的(点A , B , C的对应点分别为点 , , ),并求出三角形的面积;
⑶在x轴上确定一个格点D , 使得为直角三角形,请直接写出满足条件的所有格点D的横坐标.
22. 如图,在四边形中, , , 分别过点A、点C作、 , 垂足分别为E、F .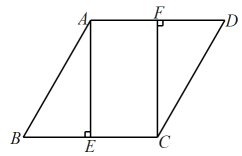 (1)、判断四边形的形状,并说明理由;(2)、若 , , 点E是的中点,求四边形的面积.23. 综合与实践
(1)、判断四边形的形状,并说明理由;(2)、若 , , 点E是的中点,求四边形的面积.23. 综合与实践【问题情境】
南宁是广西种植火龙果面积最大产量最多的区域.火龙果性甘平,营养成分丰富,包括蛋白质、酶、膳食纤维、维生素B2、维生素B3、维生素C等,果核内更含有高浓度天然色素花青素(尤以红肉为最).某学校数学兴趣小组为了解①号、②号两个品种火龙果产量情况.
【实践发现】在某火龙果果园种植基地各随机抽取25株①号、②号两个品种火龙果调查(每株火龙果每年所结的火龙果个数用a表示,共分为三个等级:不合格 , 良好 , 优秀),下面给出了部分信息:
①号品种25株果树所结火龙果个数分别为:36,47,68,82,27,27,35,46,55,48,48,57,66,57,66,58,61,75,36,57,71,47,46,71,38
②号品种25株果树所结火龙果个数处于“良好”等级包含的所有数据为:
64,54,51,62,54,63,51,63,64,54
【实践探究】
抽取的①号、②号品种火龙果树所结火龙果个数的统计表
品种
平均数
众数
中位数
方差
“优秀”等级所占百分比
①号
53
57
55
②号
53
54
x
抽取的②号品种每株果树所结火龙果个数扇形统计图
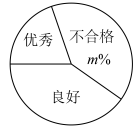 (1)、【问题解决】填空:x= , y= , m= .(2)、请用统计数据分析哪个品种的火龙果产量比较稳定,并说明理由;(3)、根据以上数据,你认为应建议果农选择哪个品种种植?请说明理由(写出一条理由即可).24. 政协第十三届广西95后政协委员赖家益,是北海市合浦县小学教师,也是北海家乡好物推荐官,他帮助当地的村民去销售当地的沃柑、红薯、海鲜等农产品,上一年仅用2天就销售完了村民种的40万斤红薯,小明家前后两次网购沃柑和红薯馈赠亲友,第一次购买沃柑6盒,红薯2盒,共花费420元;第二次购买沃柑2盒,红薯3盒,共花费210元,两次购买单价不变.(1)、求沃柑和红薯每盒各多少元?(2)、若小明家计划再次购买沃柑和红薯两种礼品共13盒,至少有两盒沃柑且要求红薯的数量不少于沃柑数量的一半,请设计出最省钱的方案,并求出最少费用.25. 如图1, , 是等边三角形,且点B、C、E在同一条直线上,连接 , .
(1)、【问题解决】填空:x= , y= , m= .(2)、请用统计数据分析哪个品种的火龙果产量比较稳定,并说明理由;(3)、根据以上数据,你认为应建议果农选择哪个品种种植?请说明理由(写出一条理由即可).24. 政协第十三届广西95后政协委员赖家益,是北海市合浦县小学教师,也是北海家乡好物推荐官,他帮助当地的村民去销售当地的沃柑、红薯、海鲜等农产品,上一年仅用2天就销售完了村民种的40万斤红薯,小明家前后两次网购沃柑和红薯馈赠亲友,第一次购买沃柑6盒,红薯2盒,共花费420元;第二次购买沃柑2盒,红薯3盒,共花费210元,两次购买单价不变.(1)、求沃柑和红薯每盒各多少元?(2)、若小明家计划再次购买沃柑和红薯两种礼品共13盒,至少有两盒沃柑且要求红薯的数量不少于沃柑数量的一半,请设计出最省钱的方案,并求出最少费用.25. 如图1, , 是等边三角形,且点B、C、E在同一条直线上,连接 , .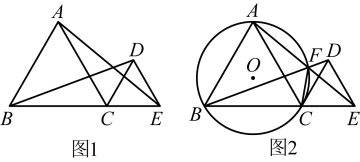 (1)、求证:;(2)、如图2,若的外接圆O交于点F , 请你证明是的切线;(3)、若 , , 求的边长.26. 如图1,抛物线交x轴于A , 两点,与y轴交于点 , 点D为线段上的一个动点,过点D作轴于点E , 交抛物线于点F , 设E点的坐标为 .
(1)、求证:;(2)、如图2,若的外接圆O交于点F , 请你证明是的切线;(3)、若 , , 求的边长.26. 如图1,抛物线交x轴于A , 两点,与y轴交于点 , 点D为线段上的一个动点,过点D作轴于点E , 交抛物线于点F , 设E点的坐标为 .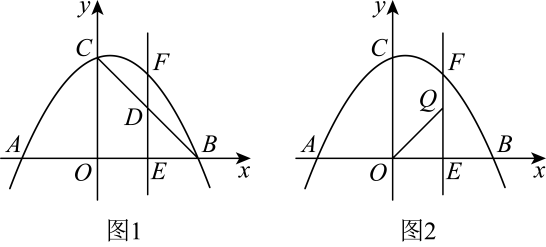 (1)、求抛物线的表达式;(2)、当m为何值时,有最大值,最大值是多少?(3)、如图2,在(2)的条件下,直线上有一动点Q , 连接 , 将线段绕点Q逆时针旋转 , 使点O的对应点P恰好落在该抛物线上,请直接写出的函数表达式.(直接写出结果)
(1)、求抛物线的表达式;(2)、当m为何值时,有最大值,最大值是多少?(3)、如图2,在(2)的条件下,直线上有一动点Q , 连接 , 将线段绕点Q逆时针旋转 , 使点O的对应点P恰好落在该抛物线上,请直接写出的函数表达式.(直接写出结果)