广西柳州柳北区、鱼峰区2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 下列各数中,最小的数是( )A、-1 B、2 C、0 D、2. 下列图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将两本相同的书进行叠放,得到如图所示的几何体,则它的正视图是( )
3. 将两本相同的书进行叠放,得到如图所示的几何体,则它的正视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列事件中,是必然事件的是( )A、疫情期间,对从疫情高风险区归来的人员进行核酸检测,检测结果为阳性 B、任意画一个三角形,其内角和为 C、某校开展“喜迎二十大,筑梦向未来”主题学习活动中,抽到A同学分享发言 D、打开电视机,正在播放“天宫课堂”5. 国产C919飞机,全称 , 是我国按照国际民航规章自行研制、具有自主知识产权的大型喷气式民用飞机,座级158-168座,最大航程达 . 数据5555000用科学记数法表示为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 若关于x的方程有两个不相等的实数根,则a的值可以是( )A、3 B、2 C、1 D、08. 实数在数轴上的对应点的位置如图所示,则正确的结论是( )
4. 下列事件中,是必然事件的是( )A、疫情期间,对从疫情高风险区归来的人员进行核酸检测,检测结果为阳性 B、任意画一个三角形,其内角和为 C、某校开展“喜迎二十大,筑梦向未来”主题学习活动中,抽到A同学分享发言 D、打开电视机,正在播放“天宫课堂”5. 国产C919飞机,全称 , 是我国按照国际民航规章自行研制、具有自主知识产权的大型喷气式民用飞机,座级158-168座,最大航程达 . 数据5555000用科学记数法表示为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 若关于x的方程有两个不相等的实数根,则a的值可以是( )A、3 B、2 C、1 D、08. 实数在数轴上的对应点的位置如图所示,则正确的结论是( ) A、 B、 C、 D、9. 如图,为的切线,A为切点,于点D , 交于点C , 平分 , 则的度数为( )
A、 B、 C、 D、9. 如图,为的切线,A为切点,于点D , 交于点C , 平分 , 则的度数为( ) A、 B、 C、 D、10. 如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , , 则的度数为( ).
A、 B、 C、 D、10. 如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , , 则的度数为( ).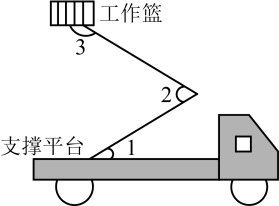 A、 B、 C、 D、11. 如图,正方形的顶点均在坐标轴上,且点的坐标为 , 以为边构造菱形 , 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2025次旋转结束时,点的对应点的坐标为( )
A、 B、 C、 D、11. 如图,正方形的顶点均在坐标轴上,且点的坐标为 , 以为边构造菱形 , 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2025次旋转结束时,点的对应点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、解答题
-
12. 如图,点A在双曲线上,连接 , 作 , 交双曲线于点B , 连接 . 若 , 则k的值为( )
 A、1 B、2 C、 D、16
A、1 B、2 C、 D、16三、填空题
-
13. 分解因式:.14. 若一次函数的图象过点 , 则 .15. 如图,一根树在离地面3米处断裂,树的顶部落在离底部4米处.树折断之前有米.
 16. 分式方程的解是 .17. 如图,这是“太极”图案的一部分,也称为“阴阳鱼”,其柔和而流畅的曲线构造既包含了国人的智慧文化,同时也蕴藏着很多的数学知识.该图案可以看作是三段弧线的组合,即以为直径的半圆弧 , 以为直径的半圆弧 , 以为直径的半圆弧 . 且满足 , A , B , C三点在同一直线上,若 , 则该图案的面积为 .
16. 分式方程的解是 .17. 如图,这是“太极”图案的一部分,也称为“阴阳鱼”,其柔和而流畅的曲线构造既包含了国人的智慧文化,同时也蕴藏着很多的数学知识.该图案可以看作是三段弧线的组合,即以为直径的半圆弧 , 以为直径的半圆弧 , 以为直径的半圆弧 . 且满足 , A , B , C三点在同一直线上,若 , 则该图案的面积为 . 18. 如图,在矩形ABCD中,AB=3,AD=4,点E是AD的中点,点P是BE上的动点,点Q是PC的中点,连接AQ , 则AQ长的最小值为 .
18. 如图,在矩形ABCD中,AB=3,AD=4,点E是AD的中点,点P是BE上的动点,点Q是PC的中点,连接AQ , 则AQ长的最小值为 .
四、解答题
-
19. 计算:20. 解不等式组 .21. 如图,已知的顶点分别为 , , .
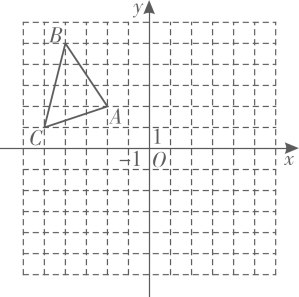 (1)、作出关于x轴对称的图形 .(2)、点P在x轴上运动,当的值最小时,求出点P的坐标.(3)、求的面积.22. 北京时间2022年12月4日,“神舟十四号”载人飞船返回舱在东风着陆场成功着陆,“神舟十四号”载人飞行任务取得圆满成功,某校为了解本校学生对航天科技的关注程度,在该校内随机选取了50名学生进行调查统计,非常关注、比较关注、一般关注和不关注四类,整理好全部调查问卷后.
(1)、作出关于x轴对称的图形 .(2)、点P在x轴上运动,当的值最小时,求出点P的坐标.(3)、求的面积.22. 北京时间2022年12月4日,“神舟十四号”载人飞船返回舱在东风着陆场成功着陆,“神舟十四号”载人飞行任务取得圆满成功,某校为了解本校学生对航天科技的关注程度,在该校内随机选取了50名学生进行调查统计,非常关注、比较关注、一般关注和不关注四类,整理好全部调查问卷后.关注程度频数统计表
类型
人数
非常关注
24
比较关注
14
一般关注
m
不关注
n
 (1)、 , ;(2)、扇形统计图中不关注对应的圆心角的度数为;(3)、若该校共有1200名学生,请估算该校学生中对航天科技比较关注和非常关注的共有多少人.23. 每年4月份,柳州的紫荆花陆续绽放,引来众多游客前往踏青观赏,纷纷拍照留念,记录生活美好时光,小王抓住这一商机,计划从市场购进A、B两种型号的手机自拍杆进行销售,据调查,购进1件A型号和1件B型号自拍杆共需45元,其中1件B型号自拍杆价格是1件A型号自拍杆价格的2倍.(1)、求1件A型号和1件B型号自拍杆的进价各是多少元?(2)、若小王计划购进A、B两种型号自拍杆共100件,并将这两款手机自拍杆分别以20元,50元的价钱进行售卖,为了保证全部售卖完后的总利润不低于1100元,求最多购进A型号自拍杆多少件?24. 综合与实践
(1)、 , ;(2)、扇形统计图中不关注对应的圆心角的度数为;(3)、若该校共有1200名学生,请估算该校学生中对航天科技比较关注和非常关注的共有多少人.23. 每年4月份,柳州的紫荆花陆续绽放,引来众多游客前往踏青观赏,纷纷拍照留念,记录生活美好时光,小王抓住这一商机,计划从市场购进A、B两种型号的手机自拍杆进行销售,据调查,购进1件A型号和1件B型号自拍杆共需45元,其中1件B型号自拍杆价格是1件A型号自拍杆价格的2倍.(1)、求1件A型号和1件B型号自拍杆的进价各是多少元?(2)、若小王计划购进A、B两种型号自拍杆共100件,并将这两款手机自拍杆分别以20元,50元的价钱进行售卖,为了保证全部售卖完后的总利润不低于1100元,求最多购进A型号自拍杆多少件?24. 综合与实践问题情境:在中, , , . 直角三角板中 , 将三角板的直角顶点放在斜边的中点处,并将三角板绕点旋转,三角板的两边 , 分别与边 , 交于点M , N .
 (1)、猜想证明:
(1)、猜想证明:如图①,在三角板旋转过程中,当点M为边的中点时,试判断四边形的形状,并说明理由;
(2)、问题解决:如图②,在三角板旋转过程中,当时,请直接写出的长;
(3)、问题解决:如图③,在三角板旋转过程中,当时,请求出线段的长.
25. 如图,是的直径,是弦,与交于点 . 的切线交的延长线于点 , 且 . (1)、求证:点是弧的中点.(2)、连接 , 取的中点 , 连接 . 若 , 求的长.26. 如图,在平面直角坐标系中,矩形OABC , 点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣ x2+bx+c经过点A和点B .
(1)、求证:点是弧的中点.(2)、连接 , 取的中点 , 连接 . 若 , 求的长.26. 如图,在平面直角坐标系中,矩形OABC , 点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣ x2+bx+c经过点A和点B . (1)、求抛物线解析式;(2)、如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE , DE , 若S△BDE=4S△ABE , 求E点坐标;(3)、如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q , 连接AP , AQ , PQ , 若△APQ为直角三角形,请直接写出P点坐标.
(1)、求抛物线解析式;(2)、如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE , DE , 若S△BDE=4S△ABE , 求E点坐标;(3)、如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q , 连接AP , AQ , PQ , 若△APQ为直角三角形,请直接写出P点坐标.
-