广东省中山市2023年中考三模数学试题
试卷更新日期:2023-06-14 类型:中考模拟
一、单选题
-
1. 0.5的相反数是( )A、0.5 B、-0.5 C、2 D、52. 如图,该几何体的左视图为( )
 A、
A、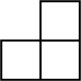 B、
B、 C、
C、 D、
D、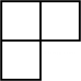 3. 六边形的内角和是( )A、360° B、540° C、720° D、900°4. 如图, , , , 则( )
3. 六边形的内角和是( )A、360° B、540° C、720° D、900°4. 如图, , , , 则( ) A、 B、 C、 D、5. 如图,矩形的对角线 , 相交于点 , 若 , , 则的周长为( )
A、 B、 C、 D、5. 如图,矩形的对角线 , 相交于点 , 若 , , 则的周长为( ) A、16 B、12 C、14 D、116. 如图,在平面直角坐标系中,点的坐标是 , 将线段绕点顺时针旋转得到线段 , 则点的坐标为( )
A、16 B、12 C、14 D、116. 如图,在平面直角坐标系中,点的坐标是 , 将线段绕点顺时针旋转得到线段 , 则点的坐标为( ) A、 B、 C、 D、7. 在一个不透明的口袋中有1个红球和4个白球,它们除颜色外其他均相同.若从袋中任取一个球,取出红球的概率为( )A、0.1 B、0.2 C、0.4 D、0.88. 下列计算正确的是( )A、 B、 C、 D、9. 若关于的一元二次方程有两个不相等的实数根,则的值可以是( )A、 B、1 C、2 D、310. 设线段长为 , 甲、乙两质点同时从点出发朝点做匀速直线运动,到达点后即停止.已知甲质点运动速度比乙质点运动速度快,且甲运动一段时间后停止一会儿又继续按原速度运动,直至到达点.如图,该图表示甲、乙之间的距离(单位:)与时间(单位:min)之间的函数关系,点横坐标为12,点坐标为 , 点横坐标为128.下列说法:①当时,;②的面积为200;③点的横坐标为200;④的最大值为216.其中正确的有( )
A、 B、 C、 D、7. 在一个不透明的口袋中有1个红球和4个白球,它们除颜色外其他均相同.若从袋中任取一个球,取出红球的概率为( )A、0.1 B、0.2 C、0.4 D、0.88. 下列计算正确的是( )A、 B、 C、 D、9. 若关于的一元二次方程有两个不相等的实数根,则的值可以是( )A、 B、1 C、2 D、310. 设线段长为 , 甲、乙两质点同时从点出发朝点做匀速直线运动,到达点后即停止.已知甲质点运动速度比乙质点运动速度快,且甲运动一段时间后停止一会儿又继续按原速度运动,直至到达点.如图,该图表示甲、乙之间的距离(单位:)与时间(单位:min)之间的函数关系,点横坐标为12,点坐标为 , 点横坐标为128.下列说法:①当时,;②的面积为200;③点的横坐标为200;④的最大值为216.其中正确的有( ) A、①② B、①③ C、②③ D、③④
A、①② B、①③ C、②③ D、③④二、填空题
-
11. 分解因式: .12. 若正比例函数的图象经过点 , 则该函数的解析式为 .13. 不等式组的解集为 .14. 如图,以点为圆心,适当长为半径画弧分别交 , 于点 , , 再分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长交于点 . 若 , , , 则 .
 15. 如图,在菱形中, , . 点E、F同时从A、C两点出发,分别沿 , 方向向点匀速移动(到点即停止).点的速度为 , 点的速度为 , 经过后恰为等边三角形,则此时的值为 .
15. 如图,在菱形中, , . 点E、F同时从A、C两点出发,分别沿 , 方向向点匀速移动(到点即停止).点的速度为 , 点的速度为 , 经过后恰为等边三角形,则此时的值为 .
三、解答题
-
16. 解方程组:17. 先化简,再求值: , 其中是方程的根.18. 某市有5个“网红”景点A , B , C , D , E及其他景点.2023年“五一”期间,该市旅游局对本市游客的旅游去向进行了随机抽查,依据调查数据制作成如图所示的统计图,请根据统计图中的信息解答下列问题:
 (1)、扇形统计图中A景点所对应的圆心角度数为;(2)、请补全条形统计图;(3)、若2023年“五一”期间有120万游客来该市旅游,试估计有多少万人去E景点旅游.19. 如图,一次函数 的图象与反比例函数 的图象交于点 和点 .
(1)、扇形统计图中A景点所对应的圆心角度数为;(2)、请补全条形统计图;(3)、若2023年“五一”期间有120万游客来该市旅游,试估计有多少万人去E景点旅游.19. 如图,一次函数 的图象与反比例函数 的图象交于点 和点 . (1)、求一次函数和反比例函数的解析式;(2)、直接写出不等式 的解集.20. 某高铁站入口的双翼闸机如图所示,它的双翼展开时,双翼边缘的端点与之间的距离为 . 双翼的边缘 , 且与闸机侧立面夹角 . 一名旅客携带一件长方体行李箱进站,行帮箱规格为(长×宽×高,单位:cm).当双翼收回进闸机箱内时,该旅客的行书箱是否可以通过闸机?请说明理由.
(1)、求一次函数和反比例函数的解析式;(2)、直接写出不等式 的解集.20. 某高铁站入口的双翼闸机如图所示,它的双翼展开时,双翼边缘的端点与之间的距离为 . 双翼的边缘 , 且与闸机侧立面夹角 . 一名旅客携带一件长方体行李箱进站,行帮箱规格为(长×宽×高,单位:cm).当双翼收回进闸机箱内时,该旅客的行书箱是否可以通过闸机?请说明理由. 21. 某文具店规定:凡一次购买练习本250本以上(含250本),可以按批发价付款;购买250本以下,只能按零售价付款.李老师来该店购买练习本,如果给学校八年级学生每人购买1本,则只能按零售价付款,需用240元;如果多购买60本,则可以按批发价付款,需用260元.(1)、求该校八年级学生人数的范围;(2)、若按批发价购买288本与按零售价购买240本所需金额相同,求该校八年级学生的人数.
21. 某文具店规定:凡一次购买练习本250本以上(含250本),可以按批发价付款;购买250本以下,只能按零售价付款.李老师来该店购买练习本,如果给学校八年级学生每人购买1本,则只能按零售价付款,需用240元;如果多购买60本,则可以按批发价付款,需用260元.(1)、求该校八年级学生人数的范围;(2)、若按批发价购买288本与按零售价购买240本所需金额相同,求该校八年级学生的人数.


