人教版八年级上册数学进阶课堂小测——11.2与三角形有关的角（三阶）

试卷更新日期：2023-06-14 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是平分线，CF交AD于点G，交BE于点H，下列结论①S_△ABE＝S_△BCE；②∠AFG＝∠AGF；③BH＝CH；④∠FAG＝2∠ACF.正确的是（　　）

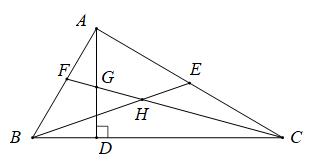A、①②③ B、③④ C、①②④ D、①②③④

查看试题解析
2. 如图，BF是∠ABD的平分线，CE是∠ACD的平分线，BF与CE交于G ，若∠BDC＝130°，∠BGC＝100°，则∠A的度数为（）

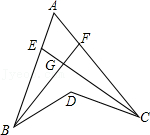A、60° B、70° C、80° D、90°

查看试题解析
3. 如图，△ABC中，∠ACB=90°，D为AB上任一点，过D作AB的垂线，分别交边AC、BC的延长线于EF两点，∠BAC∠BFD的平分线交于点I，AI交DF于点M，FI交AC于点N，连接BI.下列结论：①∠BAC=∠BFD；②∠ENI=∠EMI；③AI⊥FI；④∠ABI=∠FBI；其中正确结论的个数是（）

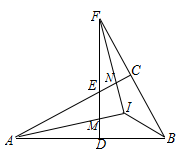A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，∠ABC=∠ACB，AD，BD，CD分别平分△ABC的外角∠EAC，内角∠ABC，外角∠ACF.以下结论：①AD∥BC，②∠ACB=2∠ADB，③∠ADC=90°-∠ABD，④BD平分∠ADC，其中正确结论有（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，已知 $△ A B C$ 的内角 $∠ A = α$ ，分别作内角 $∠ A B C$ 与外角 $∠ A C D$ 的平分线，两条平分线交于点 $A_{1}$ ，得 $∠ A_{1}$ ； $∠ A_{1} B C$ 和 $∠ A_{1} C D$ 的平分线交于点 $A_{2}$ ，得 $∠ A_{2}$ ；……以此类推得到 $∠ A_{2022}$ ，则 $∠ A_{2022}$ 的度数是（）

A、 $\frac{α}{2}$ B、 $\frac{α}{2^{2022}}$ C、 $\frac{α}{2^{2021}}$ D、 $90 + \frac{α}{2}$

查看试题解析

二、填空题

6. 如图，∠ABC＝∠ACB ， BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC ，以下结论：①AD∥BC；②DB⊥BE；③∠BDC+∠ABC＝90°；④∠A+2∠BEC＝180°．其中正确的结论有．（填序号）

查看试题解析
7. 将两张三角形纸片如图摆放，量得∠1+∠2+∠3+∠4=220°，则∠5的度数为.

查看试题解析
8. 如图，△ABC中，∠A=100°，BI、CI分别平分∠ABC，∠ACB，则∠BIC= ，若BM、CM分别平分∠ABC，∠ACB的外角平分线，则∠M= ．

查看试题解析
9. 如图，在△ABC 中，∠ABC=57°， ∠BAD=71° ，∠DAC=30° ，∠ACD=11° ，求∠DBC 的度数.

查看试题解析
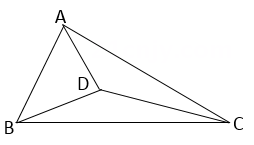10. △ABC中，∠A是最小角，∠B是最大角，且2∠B＝5∠A，若∠B的最大值m°，最小值n°，则m+n＝.

查看试题解析
11. 在△ABC中，若其中一个内角等于另外两个内角的差，则必有一个内角等于°.

查看试题解析
12. 在 $△ A B C$ 中， $∠ A B C$ ， $∠ A C B$ 的平分线交于点 $O$ ， $∠ A C B$ 的外角平分线所在直线与 $∠ A B C$ 的平分线相交于点 $D$ ，与 $∠ A B C$ 的外角平分线相交于点 $E$ ，则下列结论一定正确的是 .（填写所有正确结论的序号）
① $∠ B O C = 90 ° + \frac{1}{2} ∠ A$ ；② $∠ D = \frac{1}{2} ∠ A$ ；③ $∠ E = ∠ A$ ；④ $∠ E + ∠ D C F = 90 ° + ∠ A B D$ .

查看试题解析

三、解答题

13. 学习了平行线的判定与性质后，某兴趣小组提出如下问题：

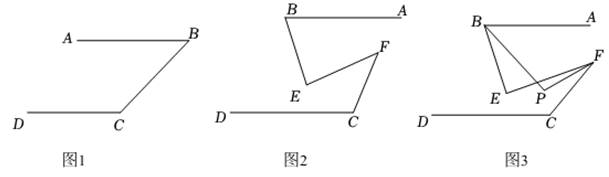
已知：如图， $AB / / CD$ ．

【初步感知】如图1，若 $∠ C = 3 ∠ B$ ，求 $∠ B$ 的度数；

【拓展延伸】如图2，当点 $E$ 、 $F$ 在两平行线之间，且在位于 $BC$ 异侧时，求证： $∠ B + ∠ E = ∠ C + ∠ F$ ；

【类比探究】如图3，若 $∠ ABE = 3 ∠ EBP$ ， $∠ CFE = 3 ∠ EFP$ ，若 $∠ E = 88 °$ ， $∠ C = 130 °$ ，直接写出 $∠ BPF$ 的度数．

查看试题解析
14.

(1)、已知直线AB∥CD，点P为平行线AB，CD之间的一点．如图1，若∠ABP=50°，∠CDP=60°，BE平分∠ABP，DE平分∠CDP，求∠BED的度数．

(2)、（探究）如图2，当点P在直线AB的上方时，若∠ABP=α，∠CDP=β，∠ABP和∠CDP的平分线交于点E₁ ， ∠ABE₁与∠CDE₁的角平分线交于点E₂ ， ∠ABE₂与∠CDE₂的角平分线交于点E₃ ， …以此类推，求∠E_n的度数．

(3)、（变式）如图3，∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，试猜想∠P与∠E的数量关系，并说明理由．

查看试题解析