沪科版数学八年级下册第19章 四边形 基础过关单元卷
试卷更新日期:2023-06-14 类型:单元试卷
一、单选题
-
1. 一个多边形的内角和与外角和相等,则它是( )A、五边形 B、四边形 C、三角形 D、不确定2. 一个n边形从一个顶点可引3条对角线,则n为( )A、6 B、5 C、4 D、33. 如图,的对角线 , 相交于点O,下列等式一定正确的是( )
 A、 B、 C、 D、4. 如图,四边形的对角线交于点 , 下列不能判定其为平行四边形的是( )
A、 B、 C、 D、4. 如图,四边形的对角线交于点 , 下列不能判定其为平行四边形的是( )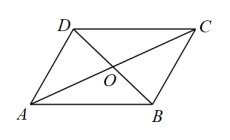 A、 B、 C、 D、5. 如图,在平行四边形中, , 连接 , 作//交延长线于点E , 过点E作交的延长线于点F , 且 , 则的长是( )
A、 B、 C、 D、5. 如图,在平行四边形中, , 连接 , 作//交延长线于点E , 过点E作交的延长线于点F , 且 , 则的长是( ) A、1 B、2 C、 D、6. 如图,在平行四边形中,与交于点O,点E是边的中点, , 则的长是( )
A、1 B、2 C、 D、6. 如图,在平行四边形中,与交于点O,点E是边的中点, , 则的长是( ) A、1 B、2 C、3 D、47. 如图,在菱形中, , , 则菱形的周长是( )
A、1 B、2 C、3 D、47. 如图,在菱形中, , , 则菱形的周长是( )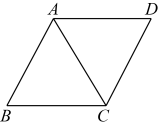 A、10 B、15 C、20 D、308. 如图,把一张长方形纸片沿对角线折叠,若 , 则长方形纸片的长宽比为( )
A、10 B、15 C、20 D、308. 如图,把一张长方形纸片沿对角线折叠,若 , 则长方形纸片的长宽比为( ) A、2:1 B、:1 C、:1 D、2:9. 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
A、2:1 B、:1 C、:1 D、2:9. 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( ) A、40cm B、30cm C、20cm D、10cm10. 用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做平面镶嵌问题.如图,利用相同边长的正三角形可以进行平面镶嵌.请问下列图形或图形组合无法进行平面镶嵌的是( )
A、40cm B、30cm C、20cm D、10cm10. 用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做平面镶嵌问题.如图,利用相同边长的正三角形可以进行平面镶嵌.请问下列图形或图形组合无法进行平面镶嵌的是( ) A、全等三角形 B、边长相等的正方形 C、边长相等的正三角形 D、边长相等的正五边形
A、全等三角形 B、边长相等的正方形 C、边长相等的正三角形 D、边长相等的正五边形二、填空题
-
11. 如果一个边形的内角和等于它的外角和的4倍,则 .12. 正十边形的对角线条数为 .13. 在中,若 , 则°.14. 如图,四边形是平行四边形,其中点 , 点 , 点 , 则点D的坐标是 .
 15. 如图,在正方形中,E,F分别是边 , 上的点, . 若 , , 则的长是 .
15. 如图,在正方形中,E,F分别是边 , 上的点, . 若 , , 则的长是 .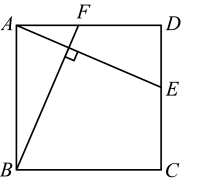
三、作图题
-
16. 如图①、图②均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B均在格点上:只用无刻度的直尺,在给定的网格中按下列要求作图,所作图形的顶点均在格点上且两图形不全等,不要求写作法.
 (1)、在图①中以线段AB为边作一个平行四边形;(2)、在图②中以线段AB为边作一个平行四边形,且有一条对角线长为2 .
(1)、在图①中以线段AB为边作一个平行四边形;(2)、在图②中以线段AB为边作一个平行四边形,且有一条对角线长为2 .四、解答题
-
17. 求图(1)(2)中x的值.
 18. 如图,在中,于点E , 于点F . 求证: .
18. 如图,在中,于点E , 于点F . 求证: .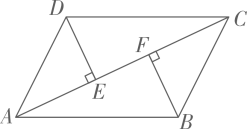 19. 如图, , 平分 , 平分 . , . 求证:四边形是矩形.
19. 如图, , 平分 , 平分 . , . 求证:四边形是矩形.
五、综合题
-
20. 小刚计算一个多边形的内角和求得结果为900°.老师指出他的计算结果不对.小刚重新检查,发现多数了一条边.(1)、你知道这个多边形是几边形吗?你是怎么知道的?(2)、这个多边形的内角和与外角和有什么样的数量关系?21. 如图所示,在▱ABCD中,点E,点F分别是AD,BC的中点,连接BE,DF.
 (1)、求证:四边形BEDF是平行四边形.(2)、若BC=2 , ∠C=105°,∠CBE=45°,求线段DF的长度.22. 已知:如图,在中,D、E、F分别是各边的中点,是高.
(1)、求证:四边形BEDF是平行四边形.(2)、若BC=2 , ∠C=105°,∠CBE=45°,求线段DF的长度.22. 已知:如图,在中,D、E、F分别是各边的中点,是高. (1)、四边形是怎样的特殊四边形?证明你的结论:(2)、问与有怎样的数量关系?证明你的结论.23. 如图,在中, , D、E、F分别是、、的中点.
(1)、四边形是怎样的特殊四边形?证明你的结论:(2)、问与有怎样的数量关系?证明你的结论.23. 如图,在中, , D、E、F分别是、、的中点. (1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.24. 如图,在Rt△ABC中,∠C=30°,AB=5,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F , 连接DE、EF .
(1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.24. 如图,在Rt△ABC中,∠C=30°,AB=5,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F , 连接DE、EF . (1)、求证:AE=DF .(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)、当t为何值时,△DEF为直角三角形?请说明理由.
(1)、求证:AE=DF .(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)、当t为何值时,△DEF为直角三角形?请说明理由.
-