沪科版数学七年级下册10.2 平行线的判定 同步测试
试卷更新日期:2023-06-14 类型:同步测试
一、单选题
-
1. 在数学课上,老师画一条直线a,按如图所示的方法,画一条直线b与直线a平行,再向上推三角尺,画一条直线c也与直线a平行,此时,发现直线b与直线c也平行,这就说明了( )
 A、如果两条直线都和第三条直线平行,那么这两条直线也互相平行 B、两直线平行,同位角相等 C、同旁内角相等,两直线平行 D、过直线外一点,有且只有一条直线与已知直线2. 在学习平行线知识时,甲同学认为“经过一点有且只有一条直线与已知直线平行”;乙同学认为“垂直于同--条直线的两条直线互相平行”,则下列判断正确的是( )A、甲正确,乙错误 B、甲错误,乙正确 C、甲乙都正确 D、甲乙都错误3. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、
A、如果两条直线都和第三条直线平行,那么这两条直线也互相平行 B、两直线平行,同位角相等 C、同旁内角相等,两直线平行 D、过直线外一点,有且只有一条直线与已知直线2. 在学习平行线知识时,甲同学认为“经过一点有且只有一条直线与已知直线平行”;乙同学认为“垂直于同--条直线的两条直线互相平行”,则下列判断正确的是( )A、甲正确,乙错误 B、甲错误,乙正确 C、甲乙都正确 D、甲乙都错误3. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、 B、
B、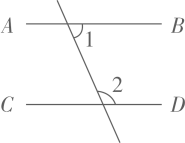 C、
C、 D、
D、 4. 如图所示,点在的延长线上,下列条件中能判断的是( )
4. 如图所示,点在的延长线上,下列条件中能判断的是( )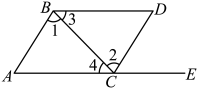 A、 B、 C、 D、5. 如图,下列结论正确的是( )
A、 B、 C、 D、5. 如图,下列结论正确的是( ) A、与是对顶角 B、与是同位角 C、与是同旁内角 D、与是内错角6. 下列图形中,和是同位角的是( )A、
A、与是对顶角 B、与是同位角 C、与是同旁内角 D、与是内错角6. 下列图形中,和是同位角的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列图形中,与互为内错角的是( )A、
7. 下列图形中,与互为内错角的是( )A、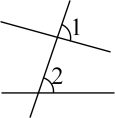 B、
B、 C、
C、 D、
D、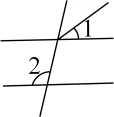 8. 如图,同旁内角是( )
8. 如图,同旁内角是( ) A、和 B、和 C、和 D、和9. 如图,直线被直线和所截,下列说法正确的是( )
A、和 B、和 C、和 D、和9. 如图,直线被直线和所截,下列说法正确的是( ) A、∠3与∠4是同旁内角 B、与是同位角 C、与是内错角 D、与是同旁内角10. 如图,下列说法错误的是( )
A、∠3与∠4是同旁内角 B、与是同位角 C、与是内错角 D、与是同旁内角10. 如图,下列说法错误的是( ) A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以
A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以二、填空题
-
11. 如图,直线、被直线所截,交点分别为M、N,则的同位角是.
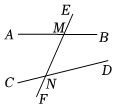 12. 如图,直线和被第三条直线所截,与成内错角的是 .
12. 如图,直线和被第三条直线所截,与成内错角的是 . 13. 如图,一共有对同旁内角.
13. 如图,一共有对同旁内角.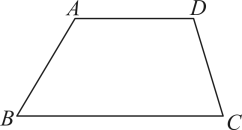 14. 张老师出了一道题目“若PC∥AB,QC∥AB.则点P,C,Q在一条直线上”,点点答出了其中的理由,你认为点点的回答是:。15. 如图,请添加一个合适的条件 , 使 .
14. 张老师出了一道题目“若PC∥AB,QC∥AB.则点P,C,Q在一条直线上”,点点答出了其中的理由,你认为点点的回答是:。15. 如图,请添加一个合适的条件 , 使 .
三、作图题
-
16. 尺规作图:如图在三角形ABC中过点A作边BC的平行线AD.(不写画法,保留作图痕迹)
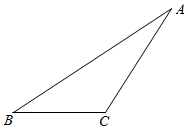
四、解答题
-
17. 已知:如图, , 和互余,于点 , 求证:.
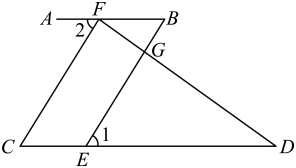 18. 如图,如果 , , 试说明与平行.请完善解答过程,并填空(理由或数学式).
18. 如图,如果 , , 试说明与平行.请完善解答过程,并填空(理由或数学式).
解:∵( )
∴( )(内错角相等,两直线平行.)
∴( )
∵(已知)
∴( )( )
∴( )
五、综合题
-
19.(1)、已知:如图 , 且 , 求证 .
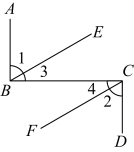
证明:∵ , (已知),
∴( ),
∵(已知)
∵( ),
∴ ▲ ,
∴( );
(2)、已知:如图,直线 , 被所截, , 求证: .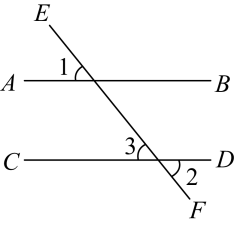
证明:∵( ),
又∵(已知),
∴ ▲ ( ),
∴( ).
20. 如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,且∠1+∠2=90°.
 (1)、求证:AB∥CD;(2)、若∠2:∠3=25,求∠BOF的度数21. 课题学习:平行线的“等角转化”功能.
(1)、求证:AB∥CD;(2)、若∠2:∠3=25,求∠BOF的度数21. 课题学习:平行线的“等角转化”功能. (1)、阅读理解:如图1,已知点A是外一点,连接、 , 求的度数.阅读并补充下面推理过程.
(1)、阅读理解:如图1,已知点A是外一点,连接、 , 求的度数.阅读并补充下面推理过程.解:过点A作 ,

▲ , ▲ ,
,
.
(2)、方法运用:如图2,已知 , 求的度数;(3)、深化拓展:已知 , 点C在点D的右侧, , 平分 , 平分 , , 所在的直线交于点E,点E在直线与之间.①如图3,点B在点A的左侧,若 , 求的度数.
②如图4,点B在点A的右侧,且 , .若 , 求度数.(用含n的代数式表示)
-