2022-2023学年沪科版数学七年级下册10.1 相交线 同步测试
试卷更新日期:2023-06-14 类型:同步测试
一、单选题
-
1. 如图,小李计划把河中的水引到水池C进行蓄水,结果发现沿线段挖渠,即 , 能使水渠最短,其中蕴含的数学原理是( )
 A、垂线段最短 B、经过一点有无数条直线 C、过两点有且仅有一条直线 D、两点之间,线段最短2. 如图, , , 则点B到直线的距离是线段( )
A、垂线段最短 B、经过一点有无数条直线 C、过两点有且仅有一条直线 D、两点之间,线段最短2. 如图, , , 则点B到直线的距离是线段( ) A、的长 B、的长 C、的长 D、的长3. 下列图形中,线段的长度能表示点到直线的距离的是( ).A、
A、的长 B、的长 C、的长 D、的长3. 下列图形中,线段的长度能表示点到直线的距离的是( ).A、 B、
B、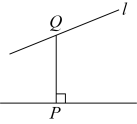 C、
C、 D、
D、 4. 下列各图中,与是对顶角的是( )A、
4. 下列各图中,与是对顶角的是( )A、 B、
B、 C、
C、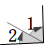 D、
D、 5. 如图,直线、相交于点 , 平分 , 若 , 则的度数为( )
5. 如图,直线、相交于点 , 平分 , 若 , 则的度数为( )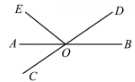 A、 B、 C、 D、6. 如图,直线AB、CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=50°,则∠AOC= ( )
A、 B、 C、 D、6. 如图,直线AB、CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=50°,则∠AOC= ( )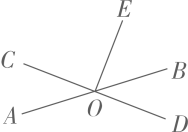 A、140° B、50° C、60° D、40°7. 如图, , , 则的度数为( )
A、140° B、50° C、60° D、40°7. 如图, , , 则的度数为( ) A、50° B、60° C、140° D、160°8. 小红在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线ln(n=1,2,3,4,5,6,7),其中l1、l2互相平行,l3、l4、I5三条直线交于一点,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个9. 平面上不重合的两点确定1条直线,不同三点最多可确定3条直线.若平面上5条直线两两相交,交点最多有a个,最少有b个,则( )A、8 B、9 C、10 D、1110. 如图,两条直线交于点 , 若 , 则的度数为( )
A、50° B、60° C、140° D、160°8. 小红在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线ln(n=1,2,3,4,5,6,7),其中l1、l2互相平行,l3、l4、I5三条直线交于一点,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个9. 平面上不重合的两点确定1条直线,不同三点最多可确定3条直线.若平面上5条直线两两相交,交点最多有a个,最少有b个,则( )A、8 B、9 C、10 D、1110. 如图,两条直线交于点 , 若 , 则的度数为( ) A、 B、 C、100 D、
A、 B、 C、100 D、二、填空题
-
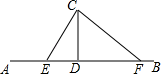
11. 已知,与互为邻补角,且 , 那么为 度12. 在同一平面内的三条直线,它们的交点个数可能是 .13. 如图, , 点E、F在上,且.则点C到的距离是.
 14. 如图,直线相交于点O, , O为垂足,如果 , 则 .
14. 如图,直线相交于点O, , O为垂足,如果 , 则 . 15. 如图,田地的旁边有一条小河 , 要想把小河里的水引到田地处,为了省时省力需要作 , 垂足为 , 沿挖水沟,则水沟最短,理由是.
15. 如图,田地的旁边有一条小河 , 要想把小河里的水引到田地处,为了省时省力需要作 , 垂足为 , 沿挖水沟,则水沟最短,理由是.
三、作图题
-
16. 如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.

⑴从火车站到码头怎样走最近?画图并说明理由;
⑵从码头到铁路怎样走最近?画图并说明理由;
⑶从火车站到河流怎样走最近?画图并说明理由.
四、解答题
-
17. 如图,直线 , 相交于点O, , 若平分且 , 求的度数.
 18. 如图,AO⊥CO,BO⊥DO,∠BOC=43°,求∠AOD和∠AOB的度数.
18. 如图,AO⊥CO,BO⊥DO,∠BOC=43°,求∠AOD和∠AOB的度数.
五、综合题
-


