2022-2023学年浙教版数学八年级下册第六章反比例函数 单元复习
试卷更新日期:2023-06-14 类型:单元试卷
一、单选题
-
1. 若反比例函数 中, 与 的值相等, 则这个相等的值为( )A、2 B、 C、 D、2. 已知反比例函数 ,当自变量 的值从3增加到6时,函数值减少了1,则函数的表达式为( )A、 B、 C、 D、3. 如图,正方形ABCO和正方形CDEF的顶点B、E在双曲线y= (x>0)上,连接OB、OE、BE,则S△OBE的值为( )
 A、2 B、2.5 C、3 D、3.54. , 是反比例函数 的图象上的两点,若 ,则下列结论正确的是( )A、 B、 C、 D、5. 已知反比例函数 , 下列结论中不正确的是( )A、其图象经过点 B、其图象分别位于第一、第三象限 C、当时, D、当时,随的增大而增大6. 如图,已知点P是双曲线上任意一点,过点P作PA⊥y轴于点A,B是x轴上一点,连接AB、PB,若△PAB的面积为2,则双曲线的解析式为( )
A、2 B、2.5 C、3 D、3.54. , 是反比例函数 的图象上的两点,若 ,则下列结论正确的是( )A、 B、 C、 D、5. 已知反比例函数 , 下列结论中不正确的是( )A、其图象经过点 B、其图象分别位于第一、第三象限 C、当时, D、当时,随的增大而增大6. 如图,已知点P是双曲线上任意一点,过点P作PA⊥y轴于点A,B是x轴上一点,连接AB、PB,若△PAB的面积为2,则双曲线的解析式为( ) A、y B、y C、y D、y7. 函数与(k、b为常数,且kb≠0)在同坐标系内的图象大致是( )A、
A、y B、y C、y D、y7. 函数与(k、b为常数,且kb≠0)在同坐标系内的图象大致是( )A、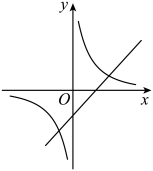 B、
B、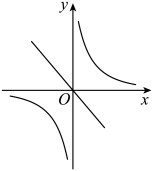 C、
C、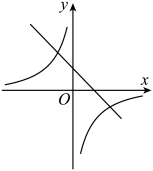 D、
D、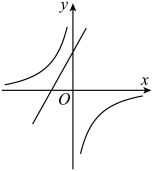 8. 如图,直线y=k1x+b与反比例函数y=(k2<0)相交于点A(-1,m),B(5,n).则不等式>k1x+b的解是( )
8. 如图,直线y=k1x+b与反比例函数y=(k2<0)相交于点A(-1,m),B(5,n).则不等式>k1x+b的解是( ) A、-1<x<0 B、-1<x<0或x>5 C、0<x<5 D、x<-1或0<x<59. 下列关系中,两个量之间为反比例关系的是( )A、正方形的面积S与边长a的关系 B、正方形的周长L与边长a的关系 C、矩形的长为a,宽为20,其面积S与a的关系 D、矩形面积为40,长为a,宽为b,a与b的关系10. 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时.x(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
A、-1<x<0 B、-1<x<0或x>5 C、0<x<5 D、x<-1或0<x<59. 下列关系中,两个量之间为反比例关系的是( )A、正方形的面积S与边长a的关系 B、正方形的周长L与边长a的关系 C、矩形的长为a,宽为20,其面积S与a的关系 D、矩形面积为40,长为a,宽为b,a与b的关系10. 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时.x(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )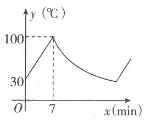 A、27min B、20min C、13min D、7min
A、27min B、20min C、13min D、7min二、填空题
-
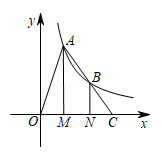
11. 若函数是反比例函数,则m的值是 .12. 把 化为 的形式为比例系数为自变量 的取值范围是.13. 如图,点A,B在反比例函数的图像上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,的面积为6,则k值为
 14. 如果点 , , 都在反比例函数 的图象上,那么 , , 的大小关系是(用“<”连接).15. 如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图像经过两点,已知平行四边形的面积是 , 则点的坐标为.
14. 如果点 , , 都在反比例函数 的图象上,那么 , , 的大小关系是(用“<”连接).15. 如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图像经过两点,已知平行四边形的面积是 , 则点的坐标为. 16. 有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 是体积 的反比例函数,它的图象如图,当 时,气体的密度是 .
16. 有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 是体积 的反比例函数,它的图象如图,当 时,气体的密度是 .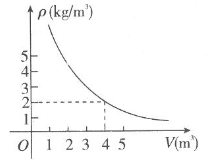 17. 设矩形的一组邻边长分别为x,y,面积是 (S为定值),当 时,矩形的周长为6,则 关于 的函数表达式是 , 自变量 的取值范围是.
17. 设矩形的一组邻边长分别为x,y,面积是 (S为定值),当 时,矩形的周长为6,则 关于 的函数表达式是 , 自变量 的取值范围是.三、综合题
-
18. 如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y= (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y= 的另一个交点.
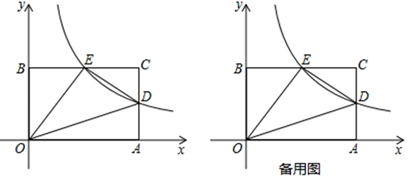 (1)、点D的坐标为 , 点E的坐标为;(2)、动点P在第一象限内,且满足
(1)、点D的坐标为 , 点E的坐标为;(2)、动点P在第一象限内,且满足①若点P在这个反比例函数的图象上,求点P的坐标;
②若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
19. 如图,一次函数的图象与反比例函数的图象交于点 , 且横坐标为1的点P也在反比例函数的图象上,另有一直线l经过点P,C. (1)、 , .(2)、求直线l的函数表达式;(3)、设直线l与y轴交于点A,将直线OC沿射线CP方向平移至点A处停止,请求出直线OC在平移过程中与x轴交点的横坐标的取值范围.20. 小明探究下列问题:商场将单价不同的甲、乙两种糖果混合成什锦糖售卖.若该商场采用以下两种不同方式混合:
(1)、 , .(2)、求直线l的函数表达式;(3)、设直线l与y轴交于点A,将直线OC沿射线CP方向平移至点A处停止,请求出直线OC在平移过程中与x轴交点的横坐标的取值范围.20. 小明探究下列问题:商场将单价不同的甲、乙两种糖果混合成什锦糖售卖.若该商场采用以下两种不同方式混合:方式1:将质量相等的甲、乙糖果进行混合;
方式2:将总价相等的甲、乙糖果进行混合.
哪种混合方式的什锦糖的单价更低?
(1)、小明设甲、乙糖果的单价分别为、 , 用含、的代数式分别表示两种混合方式的什锦糖的单价.请你写出他的解答过程;(2)、为解决问题,小明查阅了资料,发现以下正确结论:结论1:若 , 则;若 , 则;若 , 则;
结论2:反比例函数的图象上的点的横坐标与纵坐标互为倒数;
结论3:若的坐标为 , 的坐标为 , 则线段的中点坐标为 .
小明利用上述结论顺利解决此问题,请你按照他的思路写出解答过程:
①利用结论1求解;
②利用结论2、结论3求解.
21. 如图所示,在同一平面直角坐标系中,直线 与观曲线 相交于A,B两点,已知点 (1)、求 的值;(2)、求 的值.22. 如图所示,在平面直角坐标系中,反比例函数 的图象上有一点 ,过点 作 轴于点 ,将点 向右平移2个单位得到点 ,过点 作 轴的平行线交反比例函数的图象于点 .
(1)、求 的值;(2)、求 的值.22. 如图所示,在平面直角坐标系中,反比例函数 的图象上有一点 ,过点 作 轴于点 ,将点 向右平移2个单位得到点 ,过点 作 轴的平行线交反比例函数的图象于点 . (1)、点 的横坐标为(用含 的代数式表小゙)(2)、当 时,求反比例函数所对应的函数表达式.23. 如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像相交于第一、三象限内的两点,与x轴交于点C.
(1)、点 的横坐标为(用含 的代数式表小゙)(2)、当 时,求反比例函数所对应的函数表达式.23. 如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像相交于第一、三象限内的两点,与x轴交于点C. (1)、求该反比例函数和一次函数的解析式;(2)、不等式的解集是;(3)、在y轴上找一点P使最大,求的最大值及点P的坐标.24. 如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为12m2的矩形劳动基地ABCD,边AD的长不超过墙的长度,在BC边上开设宽为1m的门EF(门不需要篱笆).设AB的长为x(m),BC的长为y(m).
(1)、求该反比例函数和一次函数的解析式;(2)、不等式的解集是;(3)、在y轴上找一点P使最大,求的最大值及点P的坐标.24. 如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为12m2的矩形劳动基地ABCD,边AD的长不超过墙的长度,在BC边上开设宽为1m的门EF(门不需要篱笆).设AB的长为x(m),BC的长为y(m).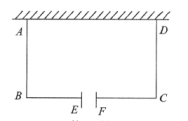 (1)、求y关于x的函数表达式.(2)、若围成矩形劳动基地ABCD三边的篱笆总长为10m,求AB和BC的长度.(3)、若AB和BC的长都是整数(单位:m),且围成矩形劳动基地ABCD三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.25. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?
(1)、求y关于x的函数表达式.(2)、若围成矩形劳动基地ABCD三边的篱笆总长为10m,求AB和BC的长度.(3)、若AB和BC的长都是整数(单位:m),且围成矩形劳动基地ABCD三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.25. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?