2022-2023学年浙教版数学八年级下册第五章特殊平行四边形 单元复习
试卷更新日期:2023-06-14 类型:单元试卷
一、单选题
-
1. 如图,矩形的对角线相交于点O, , , 则边的长为( )
 A、3 B、4 C、 D、2. 矩形具有而一般平行四边形不具有的性质是( )A、对角线相等 B、对边相等 C、对角相等 D、对角线互相垂直平分3. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.那么对于这个图中各部分的面积关系,说法不一定成立的是( )
A、3 B、4 C、 D、2. 矩形具有而一般平行四边形不具有的性质是( )A、对角线相等 B、对边相等 C、对角相等 D、对角线互相垂直平分3. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.那么对于这个图中各部分的面积关系,说法不一定成立的是( )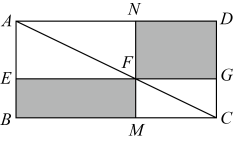 A、 B、 C、 D、4. 在矩形中,对角线、相交于点O,若 , 则等于( )A、16 B、12 C、10 D、85. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A、 B、 C、 D、4. 在矩形中,对角线、相交于点O,若 , 则等于( )A、16 B、12 C、10 D、85. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )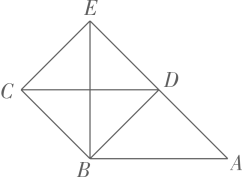 A、AB=BE B、CE⊥DE C、∠ADB=90° D、BE⊥AB6. 如图,小红在作线段的垂直平分线时,是这样操作的:分别以点A , B为圆心,大于线段长度一半的长为半径画弧,相交于点C , D , 则直线即为所求.连接 , , , , 根据她的作图方法可知,四边形定是( )
A、AB=BE B、CE⊥DE C、∠ADB=90° D、BE⊥AB6. 如图,小红在作线段的垂直平分线时,是这样操作的:分别以点A , B为圆心,大于线段长度一半的长为半径画弧,相交于点C , D , 则直线即为所求.连接 , , , , 根据她的作图方法可知,四边形定是( ) A、矩形 B、正方形 C、菱形 D、平行四边形7. 下列说法错误的是( )A、菱形的对角线互相垂直且平分 B、矩形的对角线相等 C、有一组邻边相等的四边形是菱形 D、四条边相等的四边形是菱形8. 如图,以直角三角形的三边为边向外作正方形,根据图中数据,可得出正方形A的面积是( )
A、矩形 B、正方形 C、菱形 D、平行四边形7. 下列说法错误的是( )A、菱形的对角线互相垂直且平分 B、矩形的对角线相等 C、有一组邻边相等的四边形是菱形 D、四条边相等的四边形是菱形8. 如图,以直角三角形的三边为边向外作正方形,根据图中数据,可得出正方形A的面积是( ) A、12 B、24 C、30 D、109. 《周髀算经》中有一种几何方法可以用来解形如:的方程的一个正数解,方法为:如图1,将四个长为x,宽为的长方形纸片(面积均为14)拼成一个大正方形 , 得到大正方形的面积为: , 边长 , 可依据求得是方程的一个正数解.小明按此方法解关于x的方程时,构造出类似的图形,如图2,已知正方形的面积为24,小正方形的面积为8,则方程的正数解为( )
A、12 B、24 C、30 D、109. 《周髀算经》中有一种几何方法可以用来解形如:的方程的一个正数解,方法为:如图1,将四个长为x,宽为的长方形纸片(面积均为14)拼成一个大正方形 , 得到大正方形的面积为: , 边长 , 可依据求得是方程的一个正数解.小明按此方法解关于x的方程时,构造出类似的图形,如图2,已知正方形的面积为24,小正方形的面积为8,则方程的正数解为( ) A、 B、 C、 D、10. 如图,一个由6张直角三角形纸片拼成的(不重叠、无缝隙),其中 , , 若 , 则这个平行四边形的面积为( )
A、 B、 C、 D、10. 如图,一个由6张直角三角形纸片拼成的(不重叠、无缝隙),其中 , , 若 , 则这个平行四边形的面积为( ) A、64 B、96 C、128 D、160
A、64 B、96 C、128 D、160二、填空题
-
11. 如图,矩形的对角线相交于点O , 若 , , 则的长是 .
 12. 如图,在中, , , , P为边上任意一点(点P与点C不重合),连接 , 以 , 为邻边作 , 连接 , 则长的最小值是 .
12. 如图,在中, , , , P为边上任意一点(点P与点C不重合),连接 , 以 , 为邻边作 , 连接 , 则长的最小值是 . 13. 如图,在菱形中, , , 分别为 , 的中点,是对角线上的一个动点,则的最小值是 .
13. 如图,在菱形中, , , 分别为 , 的中点,是对角线上的一个动点,则的最小值是 .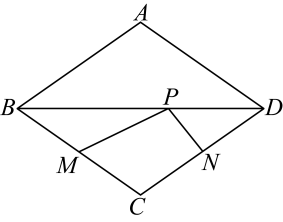 14. 如图,菱形的对角线、相交于点 , 若 , , 则菱形的边长为 .
14. 如图,菱形的对角线、相交于点 , 若 , , 则菱形的边长为 .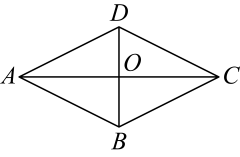 15. 如图,在正方形中,点E,F分别在边上, , , 则 .
15. 如图,在正方形中,点E,F分别在边上, , , 则 . 16. 如图,点O为正方形的中心,平分交于点E,延长到点F,使 , 连接交的延长线于点H,连接交于点G,连接.则以下四个结论中:① , ② , ③ , ④ . 正确结论为.
16. 如图,点O为正方形的中心,平分交于点E,延长到点F,使 , 连接交的延长线于点H,连接交于点G,连接.则以下四个结论中:① , ② , ③ , ④ . 正确结论为.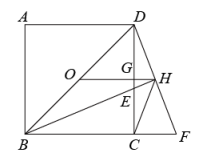
三、作图题
-
17. 如图,已知 .
 (1)、用直尺和圆规作图,作的平分线 , 交边于点E,在上方作 , 使得 , 交边于点F.(不写作法,保留作图痕迹,标注字母)(2)、在(1)的条件下,四边形是怎样的特殊四边形?证明你的结论.
(1)、用直尺和圆规作图,作的平分线 , 交边于点E,在上方作 , 使得 , 交边于点F.(不写作法,保留作图痕迹,标注字母)(2)、在(1)的条件下,四边形是怎样的特殊四边形?证明你的结论.四、解答题
-
18. 如图,矩形纸片中, , 把矩形纸片沿直线折叠,点B落在点E处,交于点F , 若 . 求的面积.
 19. 如图,在中,平分 , 交于点E , 交于点F . 求证: .
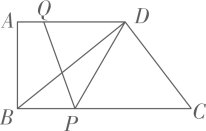
19. 如图,在中,平分 , 交于点E , 交于点F . 求证: .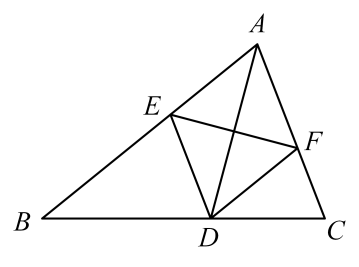 20. 如图,是一个正方形花园,公园内修建了两条小路和 , 且 , 那么这两条小路的长度相等吗?为什么?
20. 如图,是一个正方形花园,公园内修建了两条小路和 , 且 , 那么这两条小路的长度相等吗?为什么?
五、综合题
-
21. 如图所示,在直角梯形ABCD中,AD∥BC , ∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
 (1)、设△DPQ的面积为S , 求S与t之间的关系式;(2)、当t为何值时,四边形PCDQ是平行四边形?(3)、分别求出当t为何值时,①PD=PQ;②DQ=PQ .22. 如图1,小颖将一组平行的纸条折叠,点 分别落在处,线段与交于点.
(1)、设△DPQ的面积为S , 求S与t之间的关系式;(2)、当t为何值时,四边形PCDQ是平行四边形?(3)、分别求出当t为何值时,①PD=PQ;②DQ=PQ .22. 如图1,小颖将一组平行的纸条折叠,点 分别落在处,线段与交于点.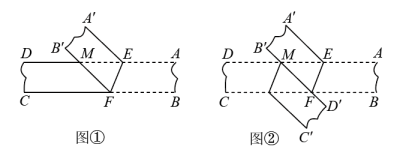 (1)、试判断的形状,并证明你的结论;(2)、如图②,将纸条的另一部分沿折叠,点 , 分别落在 , 处,且使经过点 , 试判断四边形的形状,并证明你的结论;(3)、当度时,四边形是菱形.23. 如图1,已知正方形 , 是边上的一个动点不与点、重合 , 连结 , 点关于直线的对称点为 , 连结并延长交于点 , 连结 , .
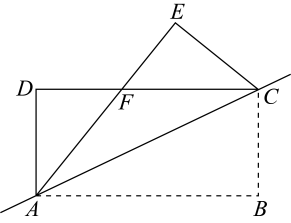
(1)、试判断的形状,并证明你的结论;(2)、如图②,将纸条的另一部分沿折叠,点 , 分别落在 , 处,且使经过点 , 试判断四边形的形状,并证明你的结论;(3)、当度时,四边形是菱形.23. 如图1,已知正方形 , 是边上的一个动点不与点、重合 , 连结 , 点关于直线的对称点为 , 连结并延长交于点 , 连结 , . (1)、求的度数.(2)、如图2,连结 , 若点为中点, , 求的面积.(3)、如图3,过点作于点 , 连结 , 请探究线段与的数量关系,并说明理由.24. 如图,直线y=﹣x+5与y轴、x轴分别交于点A,B,以AB为边在第一象限内作正方形ABCD,E是x轴上一动点,设点E坐标为(m,0)(2<m<).连接AE交BD于点F,作直线CF与y轴相交于点G.
(1)、求的度数.(2)、如图2,连结 , 若点为中点, , 求的面积.(3)、如图3,过点作于点 , 连结 , 请探究线段与的数量关系,并说明理由.24. 如图,直线y=﹣x+5与y轴、x轴分别交于点A,B,以AB为边在第一象限内作正方形ABCD,E是x轴上一动点,设点E坐标为(m,0)(2<m<).连接AE交BD于点F,作直线CF与y轴相交于点G.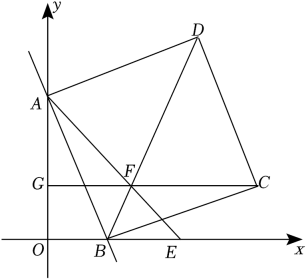 (1)、填空:点A的坐标是 , 点B的坐标是 , 点C的坐标是 , 点D的坐标是;(2)、求证:∠EAB=∠GCB;(3)、是否存在这样的m值,使GC⊥y轴?若存在,请求出此时的m值;若不存在,请说明理由.
(1)、填空:点A的坐标是 , 点B的坐标是 , 点C的坐标是 , 点D的坐标是;(2)、求证:∠EAB=∠GCB;(3)、是否存在这样的m值,使GC⊥y轴?若存在,请求出此时的m值;若不存在,请说明理由.
-