2022-2023学年浙教版数学八年级下册第四章 平行四边形 单元复习
试卷更新日期:2023-06-14 类型:单元试卷
一、单选题
-
1. 一个多边形的内角和与外角和相等,则它是( )A、五边形 B、四边形 C、三角形 D、不确定2. 在同一平面内,设a,b,c是三条互相平行的直线,已知a与b间的距离为5 cm,b与c间的距离为4 cm,则a与c间的距离为( )cm.A、1 B、9 C、4或5 D、1或93. 如图,点是的对角线上一点,连接 , , 设的面积为 , 的面积为 , 则与的大小关系( )
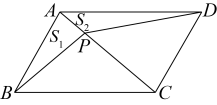 A、 B、 C、 D、无法确定4. 以下是几个银行的图标,其中是中心对称图形的是( )A、
A、 B、 C、 D、无法确定4. 以下是几个银行的图标,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,已知四边形 , 对角线和相交于 , 下面选项不能得出四边形
5. 如图,已知四边形 , 对角线和相交于 , 下面选项不能得出四边形是平行四边形的是( )
 A、 , 且 B、 , C、 , D、 , 且6. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , , 则阴影部分的面积为( )
A、 , 且 B、 , C、 , D、 , 且6. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , , 则阴影部分的面积为( ) A、24 B、17 C、13 D、107. 如图,在中,点 , 分别是 , 边上的中点,连接 , 如果 , 那么的长是( )
A、24 B、17 C、13 D、107. 如图,在中,点 , 分别是 , 边上的中点,连接 , 如果 , 那么的长是( ) A、 B、 C、 D、8. 如图,在中, , 为中线,延长至点E,使 , 连接 , F为的中点,连接 , 若 , , 则的长为( )
A、 B、 C、 D、8. 如图,在中, , 为中线,延长至点E,使 , 连接 , F为的中点,连接 , 若 , , 则的长为( )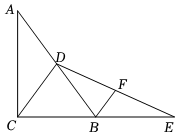 A、 B、 C、 D、9. 如图 , 平行四边形中, , 为锐角.要在对角线上找点N, , 使四边形为平行四边形,现有图中的甲、乙、丙三种方案,则正确的方案是( )
A、 B、 C、 D、9. 如图 , 平行四边形中, , 为锐角.要在对角线上找点N, , 使四边形为平行四边形,现有图中的甲、乙、丙三种方案,则正确的方案是( )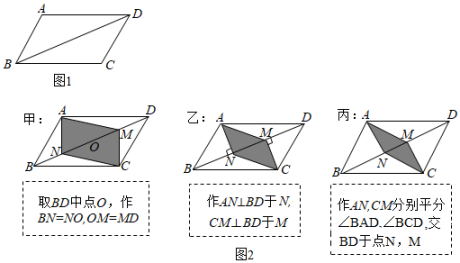 A、只有甲、乙才是 B、只有甲、丙才是 C、只有乙、丙才是 D、甲、乙、丙都是10. 用反证法证明“若实数 , 满足 , 则 , 中至少有一个是”时,应先假设( )A、 , 中至多有一个是0 B、 , 中至少有两个是0 C、 , 中没有一个是0 D、 , 都等于0
A、只有甲、乙才是 B、只有甲、丙才是 C、只有乙、丙才是 D、甲、乙、丙都是10. 用反证法证明“若实数 , 满足 , 则 , 中至少有一个是”时,应先假设( )A、 , 中至多有一个是0 B、 , 中至少有两个是0 C、 , 中没有一个是0 D、 , 都等于0二、填空题
-
11. 如果一个多边形的内角和与外角和相等,那么这个多边形的边数是 .12. 如图,在中, , , , 则 .
 13. 如图,将边长都为的正方形按如图所示的方法摆放,点分别是正方形的对称中心,则2023个这样的正方形重叠部分的面积和为 .
13. 如图,将边长都为的正方形按如图所示的方法摆放,点分别是正方形的对称中心,则2023个这样的正方形重叠部分的面积和为 . 14. 如图,中, , 若D , E是边上的两个动点,F是边上的一个动点, , 则的最小值为 .
14. 如图,中, , 若D , E是边上的两个动点,F是边上的一个动点, , 则的最小值为 . 15. 如图,在中,点D、E、F分别是边、、上的中点,且 , , 则四边形的周长等于 .
15. 如图,在中,点D、E、F分别是边、、上的中点,且 , , 则四边形的周长等于 .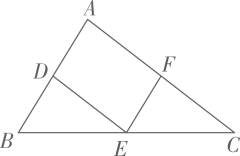 16. 如图,等腰中, , 四边形是平行四边形,连结 , , , , , 则 .
16. 如图,等腰中, , 四边形是平行四边形,连结 , , , , , 则 .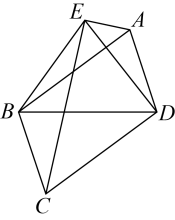
三、作图题
-
17. 图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,点A、B均在格点上,仅用无刻度的直尺在下列网格中按要求作图.
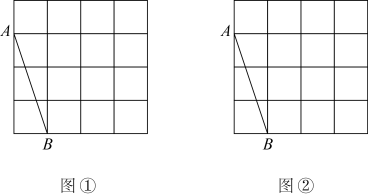 (1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.
(1)、在图①中,画出一个以AB为边的四边形ABCD,使其是中心对称图形不是轴对称图形且边长均为无理数.(2)、在图②中,画出一个以线段AB为边的四边形ABMN,使其既是轴对称图形又是中心对称图形.四、解答题
-
18. 如图,平行四边形的对角线、交于点O,点E、F在上,且求证: .
 19. 用反证法证明:等腰三角形的底角必定是锐角.20. 如图,在中,交于点E,交于点F,连接交于点M,连接交于点N,连接 . 求证 .
19. 用反证法证明:等腰三角形的底角必定是锐角.20. 如图,在中,交于点E,交于点F,连接交于点M,连接交于点N,连接 . 求证 .
五、综合题
-
21. 小刚计算一个多边形的内角和求得结果为900°.老师指出他的计算结果不对.小刚重新检查,发现多数了一条边.(1)、你知道这个多边形是几边形吗?你是怎么知道的?(2)、这个多边形的内角和与外角和有什么样的数量关系?22. 如图,在平行四边形中,对角线 , 相交于点 , 点 , 在上,点 , 在上.
 (1)、若 , , 求的度数;(2)、若四边形是平行四边形,求证: .23. 如图,在平面直角坐标系中, , , , , 并且a , b满足 . 动点P从点A出发,在线段上以每秒2个单位长度的速度向点B运动;动点Q从点O出发,在线段上以每秒1个单位长度的速度向点C运动,点P , Q分别从点A , O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t秒.
(1)、若 , , 求的度数;(2)、若四边形是平行四边形,求证: .23. 如图,在平面直角坐标系中, , , , , 并且a , b满足 . 动点P从点A出发,在线段上以每秒2个单位长度的速度向点B运动;动点Q从点O出发,在线段上以每秒1个单位长度的速度向点C运动,点P , Q分别从点A , O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t秒. (1)、直接写出B , C两点的坐标;(2)、当t为何值时,四边形是平行四边形?(3)、当t为何值时,是以为腰的等腰三角形?并求出P , Q两点的坐标.24. 中,D、E分别是 , 的中点,O是内任意一点,连接、 .
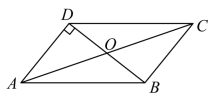
(1)、直接写出B , C两点的坐标;(2)、当t为何值时,四边形是平行四边形?(3)、当t为何值时,是以为腰的等腰三角形?并求出P , Q两点的坐标.24. 中,D、E分别是 , 的中点,O是内任意一点,连接、 .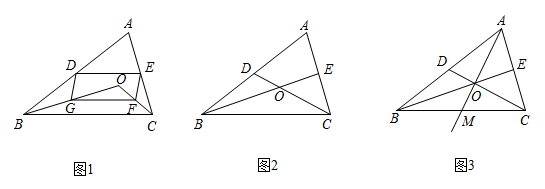 (1)、如图1,点G、F分别是、的中点,连接 , , , , 求证:四边形是平行四边形;(2)、如图2,若点O恰为和交点,求证: , ;(3)、如图3,若点O恰为和交点,射线与交于点M , 求证: .
(1)、如图1,点G、F分别是、的中点,连接 , , , , 求证:四边形是平行四边形;(2)、如图2,若点O恰为和交点,求证: , ;(3)、如图3,若点O恰为和交点,射线与交于点M , 求证: .
-