2022-2023学年浙教版数学八年级下册6.2反比例函数课后测验

试卷更新日期：2023-06-14 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 若点 $A (- 5 ， y_{1})$ ， $B (- 3 ， y_{2})$ ， $C (4 ， y_{3})$ 在反比例函数 $y = - \frac{7}{x}$ 的图像上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{1} < y_{2} < y_{3}$

查看试题解析
2. 若反比例函数 $y = \frac{k}{x}$ 的图象经过 $(2 ， 5)$ ，则下列说法正确的是（）

A、 $k = \frac{5}{2}$ B、图象在二、四象限 C、当 $x < 0$ ， y随x的增大而减小 D、当 $x > 0$ ， y随x的增大而增大

查看试题解析
3. 已知点 $(- 2 ， a)$ ； $(2 ， b)$ ； $(3 ， c)$ 在函数 $y = \frac{k}{x} (k > 0)$ 的图像上，则下列判断正确的是（）

A、 $a < b < c$ B、 $b < a < c$ C、 $a < c < b$ D、 $c < b < a$

查看试题解析
4. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点 $A (- 3 ， - \frac{1}{3})$ ，则关于 $x$ 的分式方程 $\frac{k}{x - 1} - 1 = \frac{k - 1}{x - 1}$ 的解为（）

A、 $x = - 2$ B、 $x = 2$ C、 $x = - 3$ D、 $x = 3$

查看试题解析
5. 下列说法中不正确的是（）

A、函数 $y = - 2 x$ 的图象经过原点 B、函数 $y = \frac{3}{x}$ 的图象位于第一、三象限 C、函数 $y = - \frac{2}{x}$ 的值随 $x$ 值增大而增大 D、函数 $y = 3 x - 2$ 的图象不经过第二象限

查看试题解析
6. 若点 $(- 2 ， y_{1})$ ， $(1 ， y_{2})$ ， $(3 ， y_{3})$ 在反比例函数 $y = \frac{2 + k^{2}}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{3} > y_{2} > y_{1}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{2} > y_{3} > y_{1}$

查看试题解析
7. 若点 $(- 1 ， y_{1})$ ， $(- 3 ， y_{2})$ ， $(2 ， y_{3})$ 在反比例函数 $y = \frac{k^{2} + 1}{x}$ 图象上，则下列结论正确的是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
8. 如图，A、B是反比例函数 $y = \frac{6}{x}$ 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和3．则 $△ O A B$ 的面积是（）

A、2 B、2.5 C、3 D、6

查看试题解析
9. 反比例函数 $y = \frac{k}{x}$ 的图像的两个分支分别位于第二、四象限，则一次函数 $y = k x - 2$ 的图像大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，函数 $y = - x$ 与函数 $y = - \frac{4}{x}$ 的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D．则四边形ACBD的面积为（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题（每空4分，共24分）

11. 若反比例函数 $y = \frac{m + 1}{x}$ 的图象在二、四象限，则m的取值范围为.

查看试题解析
12. 若反比例函数 $y = \frac{k}{x}$ 图象经过第一、三象限，则k的取值范围是.

查看试题解析
13. 点A（1，y₁），B（3，y₂）是反比例函数 $y = - \frac{6}{x}$ 图象上的两点，那么y₁ ， y₂的大小关系是y₁y₂ ．（填“＞”或“＜”）

查看试题解析
14. 已知反比例函 $y = \frac{k - 1}{x}$ ，在每个象限内y随x的增大而增大，则k的取值范围为．

查看试题解析
15. 如图，点A是反比例函数 $y = \frac{6}{x} (x > 0)$ 上的一点，过点A作 $A C ⊥ y$ 轴，垂足为点C， $A C$ 交反比例函数 $y = \frac{2}{x}$ 的图象于点B，点P是x轴上的动点，则 $△ P A B$ 的面积为．

查看试题解析
16. 点 $P (2 ， 4)$ 在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，则反比例函数的解析式为.

查看试题解析

三、综合题（共8题，共66分）

17. 已知反比例函数 $y = - \frac{3}{x}$ .

(1)、若 $x > 1$ ，则 $y$ 的取值范围为.

(2)、若 $x ⩽ 3$ 且 $x \neq 0$ ，则 $y$ 的取值范围为.

(3)、若 $y > 1$ ，则自变量 $x$ 的取值范围为.

查看试题解析
18. 已知 $A (2 ， 1)$ 、 $B (a ， b)$ 是反比例函数 $y = \frac{k}{x}$ 的图象上的点．

(1)、求 $k$ 的值；

(2)、求证： $a^{2} + b^{2} \geq 4$ ．

查看试题解析
19. 如图，在平面直角坐标系中，已知点 $A (8 ， 1)$ ， $B (0 ， - 3)$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点A，动直线 $x = t (0 < t < 8)$ 与反比例函数的图象交于点M，与直线 $A B$ 交于点N.

(1)、求k的值；

(2)、当 $t = 4$ 时，求 $△ B M A$ 面积.

查看试题解析
20. 如图，点 $A$ 、 $B$ 分别在反比例函数 $y_{1} = \frac{k_{1}}{x} (x > 0)$ 和 $y_{2} = \frac{k_{2}}{x} (x > 0)$ 的图象上，线段 $A B$ 与 $x$ 轴相交于点 $P$ ．

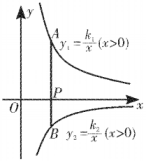
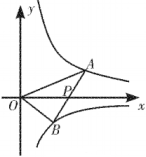
图① 图②

(1)、如图①，若 $A B ⊥ x$ 轴，且 $| A P | = 2 | P B |$ ， $k_{1} + k_{2} = 1$ ．求 $k_{1}$ 、 $k_{2}$ 的值；

(2)、如图②，若点 $P$ 是线段 $A B$ 的中点，且 $△ O A B$ 的面积为2．求 $k_{1} - k_{2}$ 的值．

查看试题解析
21. 综合与探究
如图，已知， $A (0 ， 4)$ ， $B (- 3 ， 0)$ ， $C (2 ， 0)$ ， D为B点关于 $A C$ 的对称点，反比例函数 $y = \frac{k}{x}$ 的图象经过D点．

(1)、证明四边形 $A B C D$ 为菱形；

(2)、求此反比例函数的解析式；

(3)、已知在 $y = \frac{k}{x}$ 的图象（ $x > 0$ ）上有一点N，y轴正半轴上有一点M，且四边形 $A B M N$ 是平行四边形，求M点的坐标．

查看试题解析
22. 如图，经过坐标原点O的直线交反比例函数 $y = \frac{k}{x} (k ＜ 0)$ 的图象于点A（﹣2，3），B．点C是x轴上异于点O的动点，点D与点C关于y轴对称，射线AC交y轴于点E，连结AD，BC，BD．

(1)、①写出点B的坐标．
②求证：四边形ACBD是平行四边形．

(2)、当四边形ACBD是矩形时，求点C的坐标．

(3)、点C在运动过程中，当A，C，E三点中的其中一点到另两点的距离相等时，求 $\frac{O E}{B C}$ 的值．

查看试题解析
23. 如图，菱形ABCD的顶点A、B分别在y轴与x轴正半轴上，C、D在第一象限， $A C ∥ x$ 轴，反比例函数 $y = \frac{k}{x}$ 的图象经过顶点D．

(1)、若 $A (0 ， 2)$ ， $B (1 ， 0)$
①求反比例函数的解析式；

②证明：点C落在反比例函数 $y = \frac{k}{x}$ 的图象上；

(2)、若 $k = 18 \sqrt{3}$ ， $∠ A B D = 30 °$ ，求菱形ABCD的边长．

查看试题解析
24. 如图，点M（0，m）为y轴上一点，m＜0，过点M作y轴的垂线l，与反比例函数 $y = \frac{1}{x}$ 的图象交于点P.把直线l下方反比例函数的图象沿着直线l翻折，其它部分保持不变，所形成的新图象称为“G图象”.

(1)、当m＝－1时，求“G图象”与x轴交点横坐标；

(2)、过y轴上另一点N（0，n）作y轴垂线，与“G图象”交于点A、B.
①若n＝2，且AN＝2BN，求m的值；
②若AN＝2BN，求m与n的数量关系.

查看试题解析

2022-2023学年浙教版数学八年级下册6.2反比例函数 课后测验

一、单选题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、综合题（共8题，共66分）

2022-2023学年浙教版数学八年级下册6.2反比例函数课后测验