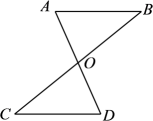(人教版)吉林地区七年级升八年级2023年暑假衔接 专题9 全等三角形的判定
试卷更新日期:2023-06-13 类型:同步测试
一、单选题
-
1. 如图是用尺规作的平分线的示意图,那么这样作图的依据是( )
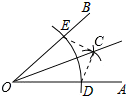 A、SSS B、SAS C、ASA D、AAS2. 如图,有一块三角形的玻璃,不小心掉在地上打成三块,现要到玻璃店重新划一块与原来形状、大小一样的玻璃,只需带到玻璃店( )
A、SSS B、SAS C、ASA D、AAS2. 如图,有一块三角形的玻璃,不小心掉在地上打成三块,现要到玻璃店重新划一块与原来形状、大小一样的玻璃,只需带到玻璃店( ) A、① B、② C、③ D、①、②、③其中任一块3. 如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
A、① B、② C、③ D、①、②、③其中任一块3. 如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( ) A、∠A=∠D B、AC=DB C、∠ABC=∠DCB D、AB=DC4. 如图,已知 , 以点B为圆心,适当长为半径作弧,分别交于D,P;作一条射线 , 以点F圆心,长为半径作弧l,交于点H;以H为圆心,长为半径作弧,交弧于点Q;作射线.这样可得 , 其依据是( )
A、∠A=∠D B、AC=DB C、∠ABC=∠DCB D、AB=DC4. 如图,已知 , 以点B为圆心,适当长为半径作弧,分别交于D,P;作一条射线 , 以点F圆心,长为半径作弧l,交于点H;以H为圆心,长为半径作弧,交弧于点Q;作射线.这样可得 , 其依据是( ) A、 B、 C、 D、5. 如图, , 那么添加下列选项中的一个条件后,仍无法判定的是( )
A、 B、 C、 D、5. 如图, , 那么添加下列选项中的一个条件后,仍无法判定的是( )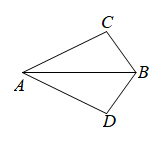 A、 B、 C、 D、6. 如图,点E、F在线段AC上,AF=CE,AD=CB,下列不能推断△ADF≌△CBE是( )
A、 B、 C、 D、6. 如图,点E、F在线段AC上,AF=CE,AD=CB,下列不能推断△ADF≌△CBE是( ) A、∠D=∠B B、∠A=∠C C、BE=DF D、AD//BC7. 如图,点E、F在上, , , 相交于点G,添加下列哪一个条件,可使得( )
A、∠D=∠B B、∠A=∠C C、BE=DF D、AD//BC7. 如图,点E、F在上, , , 相交于点G,添加下列哪一个条件,可使得( ) A、 B、 C、 D、8. 如图,已知 , 添加下列条件不能判定的是( )
A、 B、 C、 D、8. 如图,已知 , 添加下列条件不能判定的是( ) A、 B、 C、 D、9. 如图,在中, , , , 一条线段 , , 两点分别在线段和的垂线上移动,若以 , , 为顶点的三角形与以 , , 为顶点的三角形全等,则的值为( )
A、 B、 C、 D、9. 如图,在中, , , , 一条线段 , , 两点分别在线段和的垂线上移动,若以 , , 为顶点的三角形与以 , , 为顶点的三角形全等,则的值为( ) A、6cm B、12cm C、12cm或6cm D、以上答案都不对10. 如图, , , , 则不正确的结论是( )
A、6cm B、12cm C、12cm或6cm D、以上答案都不对10. 如图, , , , 则不正确的结论是( ) A、与互为余角 B、 C、≌ D、
A、与互为余角 B、 C、≌ D、二、填空题
-
11. 如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知 , , 则两张凳子的高度之和为.
 12. 如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为°.
12. 如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为°.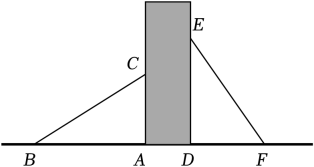 13. 如图,已知 , 要证明 , 还需添加的一个条件是 .(只填一个条件即可)
13. 如图,已知 , 要证明 , 还需添加的一个条件是 .(只填一个条件即可) 14. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm .
14. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm . 15. 如图,在中, , D,E,F分别是边 , , 上的点,且 , . 若 , 则的度数为°.
15. 如图,在中, , D,E,F分别是边 , , 上的点,且 , . 若 , 则的度数为°.
三、解答题
-
16. 如图,在和中,点、、在一条直线上, , , .求证:.
 17. 如图,已知在△ABC和△DBE中,AB=DB,∠1=∠2,∠A=∠D.求证:BC=BE.
17. 如图,已知在△ABC和△DBE中,AB=DB,∠1=∠2,∠A=∠D.求证:BC=BE.
 18. 已知:如图,点在同一条直线上,.求证:.
18. 已知:如图,点在同一条直线上,.求证:. 19. 已知:如图,点B,F,C,E在一条直线上, , , 且.求证:.
19. 已知:如图,点B,F,C,E在一条直线上, , , 且.求证:.
四、综合题
-
20. 如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
 (1)、求证:AC∥DE;(2)、若BF=21,EC=9,求BC的长.
(1)、求证:AC∥DE;(2)、若BF=21,EC=9,求BC的长.