(人教版)吉林地区七年级升八年级2023年暑假衔接 专题8 全等三角形
试卷更新日期:2023-06-13 类型:同步测试
一、单选题
-
1. 如图, , A的对应顶点是B,C的对应顶点是D,若 , , , 则的长为( )
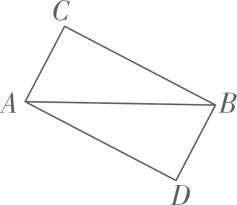 A、3 B、7 C、8 D、以上都不对2. 如图,点A,B,C,D在同一条直线上,且 , , , 若 , 则的度数为( )
A、3 B、7 C、8 D、以上都不对2. 如图,点A,B,C,D在同一条直线上,且 , , , 若 , 则的度数为( ) A、 B、 C、 D、3. 如图 , , . 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为 . 当与全等时,的值是( )
A、 B、 C、 D、3. 如图 , , . 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为 . 当与全等时,的值是( )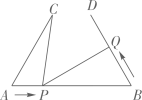 A、2 B、1或 C、2或 D、1或24. 如图,已知 , 若 , 则的度数为( )
A、2 B、1或 C、2或 D、1或24. 如图,已知 , 若 , 则的度数为( ) A、80° B、90 C、100° D、1105. 如图, , 若 , 则的度数是( )
A、80° B、90 C、100° D、1105. 如图, , 若 , 则的度数是( ) A、80° B、70° C、65° D、60°6. 如图,△ABC≌△DEF,若∠A=100°,∠F=47°,则∠E的度数为( )
A、80° B、70° C、65° D、60°6. 如图,△ABC≌△DEF,若∠A=100°,∠F=47°,则∠E的度数为( )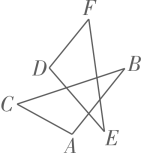 A、100° B、53° C、47° D、33°7. 如图, , 若 , 则的度数为( )
A、100° B、53° C、47° D、33°7. 如图, , 若 , 则的度数为( ) A、20° B、25° C、30° D、50°8. 如图,点A,E,C在同一直线上, , , , 则BC的长为( )
A、20° B、25° C、30° D、50°8. 如图,点A,E,C在同一直线上, , , , 则BC的长为( ) A、3 B、5 C、8 D、119. 如图,若 , 则等于( )
A、3 B、5 C、8 D、119. 如图,若 , 则等于( ) A、 B、 C、 D、10. 如图, , 若 , , 则的度数为( )
A、 B、 C、 D、10. 如图, , 若 , , 则的度数为( )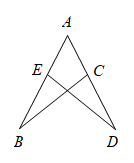 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知△ACE≌△DBF,∠A=66°,∠E=78°,则∠FBD的度数为
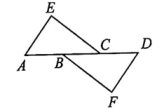 12. 如图, , 如果 , 则的长是 .
12. 如图, , 如果 , 则的长是 .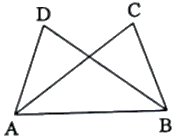 13. 如图:△ABC≌△DEF,BC=7,EC=4,那么CF的长为 .
13. 如图:△ABC≌△DEF,BC=7,EC=4,那么CF的长为 . 14. 如图,已知 ABD≌ ACE,∠A=53°,∠B=21°,则∠BEC=°.
14. 如图,已知 ABD≌ ACE,∠A=53°,∠B=21°,则∠BEC=°.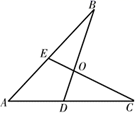 15. 如图,若 , , , 则的长是 .
15. 如图,若 , , , 则的长是 .
三、解答题
-
16. 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=CE.求证:AC∥DF.
 17. 如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.求∠F的度数与DH的长
17. 如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.求∠F的度数与DH的长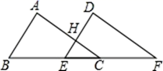 18. 如图,已知 , 点D在上,与交于点P.若 , , 求的度数.
18. 如图,已知 , 点D在上,与交于点P.若 , , 求的度数. 19. 如图,点D在上,点E在上, , 求证: .
19. 如图,点D在上,点E在上, , 求证: .
四、综合题
-
20. 如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
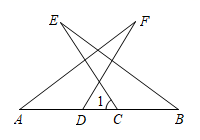 (1)、∠1的度数;
(1)、∠1的度数;
(2)、AC的长.


