(人教版)吉林地区七年级升八年级2023年暑假衔接 专题5 三角形的外角
试卷更新日期:2023-06-13 类型:同步测试
一、单选题
-
1. 下列说法正确的是( )A、如果两个角相等,那么这两个角是对顶角 B、三角形的一个外角大于任何一个内角 C、在同一平面内,经过一点有且只有一条直线与已知直线平行 D、从直线外一点到这条直线上的垂线段的长度,叫做点到直线的距离2. 如图, , , 连接 , 若 , 则的度数为 ( )
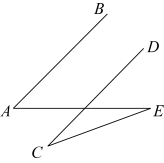 A、 B、 C、 D、3. 如图,将一副直角三角板,按如图所示叠放在一起,则图中的度数是( )
A、 B、 C、 D、3. 如图,将一副直角三角板,按如图所示叠放在一起,则图中的度数是( ) A、 B、 C、 D、4. 如图, , 则的度数( )
A、 B、 C、 D、4. 如图, , 则的度数( )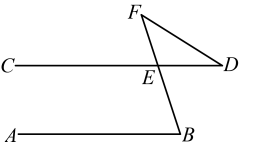 A、 B、 C、 D、5. 将一块三角板和一块直尺如图放置,若 , 则的度数为( )
A、 B、 C、 D、5. 将一块三角板和一块直尺如图放置,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,直线 , 直线c交直线a于点A,交直线b于点B,直线c,若 , 则的度数为( )
A、 B、 C、 D、6. 如图,直线 , 直线c交直线a于点A,交直线b于点B,直线c,若 , 则的度数为( ) A、100° B、120° C、130° D、160°7. 如图平行四边 , 对角线相交于O点,∠ACB=30°,∠AOB=45°,∠DBC=( )
A、100° B、120° C、130° D、160°7. 如图平行四边 , 对角线相交于O点,∠ACB=30°,∠AOB=45°,∠DBC=( ) A、 B、 C、 D、8. 如图,直线 , 的顶点C在直线b上,边与直线b相交于点D.若是等边三角形, , 则( )
A、 B、 C、 D、8. 如图,直线 , 的顶点C在直线b上,边与直线b相交于点D.若是等边三角形, , 则( ) A、 B、 C、 D、9. 图1是一路灯的实物图,图2是该路灯的平面示意图, , , 则图2中的度数为( )
A、 B、 C、 D、9. 图1是一路灯的实物图,图2是该路灯的平面示意图, , , 则图2中的度数为( ) A、 B、 C、 D、10. 如图,是的一个外角,E是边AB上一点,下列结论错误的是( )
A、 B、 C、 D、10. 如图,是的一个外角,E是边AB上一点,下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一副三角尺,按如图所示叠放在一起,则图中的度数为.
 12. 如图,在中,延长至D,延长至E,如果 , 则 .
12. 如图,在中,延长至D,延长至E,如果 , 则 . 13. 如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=50°,则∠BOE的度数为.
13. 如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=50°,则∠BOE的度数为. 14. 如图,在中,点在边上, . 若 , 则的大小为度.
14. 如图,在中,点在边上, . 若 , 则的大小为度.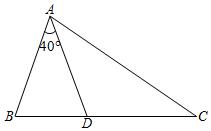 15. 如图,把一副三角板的两个直角三角形叠放在一起,则α的度数为 .
15. 如图,把一副三角板的两个直角三角形叠放在一起,则α的度数为 .
三、解答题
-
16. 如图,在中, , , 的外角的平分线交的延长线于点E.求的度数.
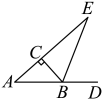 17. 如图, , , 平分 , 求的度数.
17. 如图, , , 平分 , 求的度数. 18. 如图,在中,平分 , , .求 , 的度数.
18. 如图,在中,平分 , , .求 , 的度数.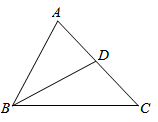 19. 如图, , , , 求的度数.
19. 如图, , , , 求的度数.
四、综合题
-
20. 已知中,于点D,AE平分 , 过点A作直线 , 且 , .
 (1)、求的外角的度数;(2)、求的度数.
(1)、求的外角的度数;(2)、求的度数.


