(人教版)吉林地区七年级升八年级2023年暑假衔接 专题4 三角形的内角
试卷更新日期:2023-06-13 类型:同步测试
一、单选题
-
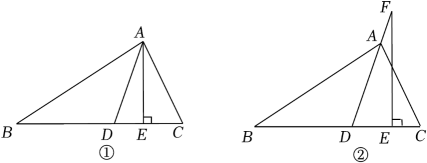
1. 若三角形三个内角度数比为 , 则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定2. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°3. 如图,在中, , 是的高线,是的角平分线,则的度数是( )
 A、 B、 C、 D、4. 如图,在中, , 的度数为α.点P在边上(点P不与点B,点C重合),作于点D,连接 , 取上一点E,使得 , 连接 , 并延长交于点F之后,有 . 若记的度数为x,则下列关于的表达式正确的是( )
A、 B、 C、 D、4. 如图,在中, , 的度数为α.点P在边上(点P不与点B,点C重合),作于点D,连接 , 取上一点E,使得 , 连接 , 并延长交于点F之后,有 . 若记的度数为x,则下列关于的表达式正确的是( )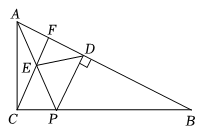 A、 B、 C、 D、5. 如图,在中,、的平分线 , 相交于点F, , 则( )
A、 B、 C、 D、5. 如图,在中,、的平分线 , 相交于点F, , 则( )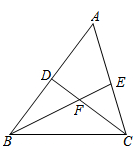 A、 B、 C、 D、6. 如图,在中, , 中线与角平分线相交于点 , 已知 , 则的度数为( )
A、 B、 C、 D、6. 如图,在中, , 中线与角平分线相交于点 , 已知 , 则的度数为( )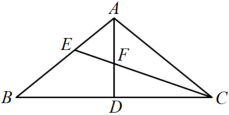 A、 B、 C、 D、7. 一个三角形可以被剖分为两个等腰三角形,已知原三角形的一个内角为36°,则原三角形最大内角的所有可能值的总和是( )A、 B、 C、 D、8. 如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )
A、 B、 C、 D、7. 一个三角形可以被剖分为两个等腰三角形,已知原三角形的一个内角为36°,则原三角形最大内角的所有可能值的总和是( )A、 B、 C、 D、8. 如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )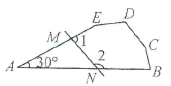 A、210° B、110° C、150° D、100°9. 如下图, , BP、CP分别平分∠ABC和∠ACB,则∠P的度数是( )
A、210° B、110° C、150° D、100°9. 如下图, , BP、CP分别平分∠ABC和∠ACB,则∠P的度数是( ) A、125° B、115° C、110° D、35°10. 如图,在△ABC中,AD是高,AE是角平分线,AF是中线.则下列结论错误的是( )
A、125° B、115° C、110° D、35°10. 如图,在△ABC中,AD是高,AE是角平分线,AF是中线.则下列结论错误的是( ) A、BF=CF B、∠BAF=∠CAF C、∠B+∠BAD=90° D、
A、BF=CF B、∠BAF=∠CAF C、∠B+∠BAD=90° D、二、填空题
-
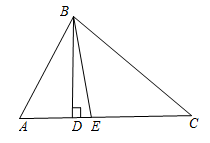
11. 如图,直线 , 且于点C,若 , 则的度数为.
 12. 如图,是的角平分线, , 垂足为 , 连结 . 若 , , 则的度数为 .
12. 如图,是的角平分线, , 垂足为 , 连结 . 若 , , 则的度数为 . 13. 已知△ABC中,∠A=∠B=∠C,则△ABC是 三角形.14. 将一副三角尺按如图所示的方式叠放在一起,则图中的度数是 .
13. 已知△ABC中,∠A=∠B=∠C,则△ABC是 三角形.14. 将一副三角尺按如图所示的方式叠放在一起,则图中的度数是 . 15. 如图,在中,平分 , 于点E, , , 则°.
15. 如图,在中,平分 , 于点E, , , 则°.
三、解答题
-
16. 如图,在中, , , 平分交于点M,求证: .
 17. 如图:已知在△ABC中,AD平分∠BAC,AE⊥BC,垂足为E,∠B=38°,∠C=70°,求∠DAE的度数.
17. 如图:已知在△ABC中,AD平分∠BAC,AE⊥BC,垂足为E,∠B=38°,∠C=70°,求∠DAE的度数.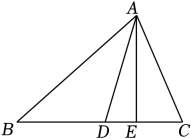 18. 如图,在△ABC中,AD⊥BC,垂直为D,∠1=∠B,∠C=67°,求∠BAC的度数
18. 如图,在△ABC中,AD⊥BC,垂直为D,∠1=∠B,∠C=67°,求∠BAC的度数 19. 如图,中,点D在边上, , E为的中点, , 求的度数.
19. 如图,中,点D在边上, , E为的中点, , 求的度数.
四、综合题
-
20. 如图,AE平分∠BAC,∠CAE=∠CEA.
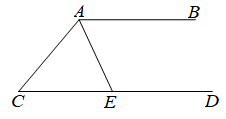 (1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.21. 如图
(1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.21. 如图 (1)、如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30︒,则∠ABC+∠ACB=︒,∠XBC+∠XCB=︒(2)、如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
(1)、如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30︒,则∠ABC+∠ACB=︒,∠XBC+∠XCB=︒(2)、如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.