(人教版)吉林地区七年级升八年级2023年暑假衔接 专题2 三角形的高、中线与角平分线
试卷更新日期:2023-06-13 类型:同步测试
一、单选题
-
1. 如图,从各顶点作平行线 , 各与其对边或其延长线相交于点D,E,F.若的面积为 , 的面积为 , 的面积为 , 只要知道下列哪个值就可以求出的面积( )
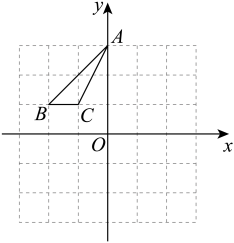
 A、 B、 C、 D、2. 如图,的顶点A,B,C在边长为1的正方形网格的格点上,则边上的高为( )
A、 B、 C、 D、2. 如图,的顶点A,B,C在边长为1的正方形网格的格点上,则边上的高为( ) A、 B、 C、 D、3. 利用直角三角板,作的高线,下列作法正确的是( )A、
A、 B、 C、 D、3. 利用直角三角板,作的高线,下列作法正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,是的中线,点是上一点,若 , , 则的长为( )
4. 如图,是的中线,点是上一点,若 , , 则的长为( ) A、5 B、6 C、7 D、85. 如图,D、E分别是BC、AC的中点, , 则的面积为( )
A、5 B、6 C、7 D、85. 如图,D、E分别是BC、AC的中点, , 则的面积为( ) A、4 B、8 C、10 D、126. 如图,是的中线, , 则的长为( )
A、4 B、8 C、10 D、126. 如图,是的中线, , 则的长为( )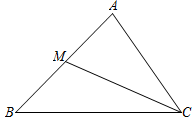 A、 B、 C、 D、7. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是4,则△BEF的面积等于( )
A、 B、 C、 D、7. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是4,则△BEF的面积等于( ) A、0.75 B、1.25 C、2 D、18. 下列图形中,线段表示的高线的是( )A、
A、0.75 B、1.25 C、2 D、18. 下列图形中,线段表示的高线的是( )A、 B、
B、 C、
C、 D、
D、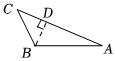 9. 如图,的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高为( )
9. 如图,的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高为( )
 A、 B、 C、 D、10. 如图,是的的中线,是的△的中线,若的面积为 , 则的面积为( )
A、 B、 C、 D、10. 如图,是的的中线,是的△的中线,若的面积为 , 则的面积为( )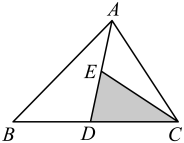 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,的三条中线AD,BE,CF交于点O,若的面积为20,那么阴影部分的面积之和为.
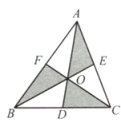 12. 如图中,已知D、E、F分别是BC、AD、CE的中点,且 , 那么阴影部分的面积为.
12. 如图中,已知D、E、F分别是BC、AD、CE的中点,且 , 那么阴影部分的面积为. 13. 已知、是的高,直线、相交所成的锐角为40°,则的度数是 .14. 如图,是的中线,是的中线,若 , 则 .
13. 已知、是的高,直线、相交所成的锐角为40°,则的度数是 .14. 如图,是的中线,是的中线,若 , 则 .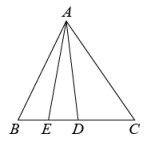 15. 如图,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△AEF=4 cm2 , 则△ABC的面积为cm2 .
15. 如图,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△AEF=4 cm2 , 则△ABC的面积为cm2 .
三、解答题
-
16. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
 17. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.
17. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数. 18. 如图,在中, , 点D是的中点,点E在上, , 若 , 求的度数.
18. 如图,在中, , 点D是的中点,点E在上, , 若 , 求的度数. 19. 如图,中, , 为边上的高,平分 , 且分别交 , 于点 , . 求证: .
19. 如图,中, , 为边上的高,平分 , 且分别交 , 于点 , . 求证: .
四、综合题
-
20. 如图,在四边形中, , 平分 , .
 (1)、画出的高;(2)、的面积等于 .
(1)、画出的高;(2)、的面积等于 .