（人教版）吉林地区七年级升八年级2023年暑假衔接专题1 三角形的边

试卷更新日期：2023-06-13 类型：同步测试

进入出卷网下载

一、单选题

1. 两根长度分别为2，10的木棒，若想钉一个三角形木架，第三根木棒的长度可以是（）

A、13 B、10 C、7 D、6

查看试题解析
2. 若长度为x，2，3的三条线段能组成一个三角形，则x的值可能为（　　）

A、6 B、5 C、1 D、3

查看试题解析
3. 三角形的两边长分别为 $4 c m$ 和 $7 c m$ ，此三角形第三边长可能是（）

A、 $2 c m$ B、 $3 c m$ C、 $6 c m$ D、 $11 c m$

查看试题解析
4. 乐乐要从下面四组木棒中选择一组制作一个三角形作品，你认为他应该选（）

A、3，5，6 B、2，3，5 C、2，4，7 D、3，8，4

查看试题解析
5. 两根木棒的长度分别为5cm，8cm，取第三根木棒，使它们首尾顺次相接组成一个三角形，则第三根木棒的长度可以是（）

A、2cm B、3cm C、6cm D、15cm

查看试题解析
6. 嘉兴某校项目化学习小组研究“三角形周长”的课题，将3根木棒首尾相连围成一个三角形，其中两根木棒的长分别为3cm、10cm，则该三角形的周长可能是（）

A、18cm B、19cm C、20cm D、21cm

查看试题解析
7. 为估计池塘两岸A、B间的距离，如图，小明在池塘一侧选取了点O，测得 $O A = 8 m ， O B = 15 m$ ，那么A、B间的距离不可能是（）

A、 $7 m$ B、 $13 m$ C、 $14 m$ D、 $15 m$

查看试题解析
8. 已知 $△ A B C$ 中， $A B = 3$ ， $B C = 4$ ，则第三边AC的取值范围是（）

A、 $3 < A C < 4$ B、 $0 < A C < 12$ C、 $1 \leq A C \leq 7$ D、 $1 < A C < 7$

查看试题解析
9. 在 $△ A B C$ 中， $A B = 2 n - 5$ ， $A C = 4$ ， $B C = 13$ ，则 $n$ 的取值范围是（）

A、 $n < 11$ B、 $7 < n < 11$ C、 $9 < n < 17$ D、 $n > 7$

查看试题解析
10. 如图，在△ABC中，AD为BC边上的中线，若AB＝4，AC＝2，则AD的取值范围是（）

A、1＜AD＜3 B、2＜AD＜4 C、2＜AD＜6 D、2＜AD＜3

查看试题解析

二、填空题

11. 周长为30，各边互不相等且都是整数的三角形共有个．

查看试题解析
12. 已知a，b，c是 $△ A B C$ 的三边长，a，b满足 $| a - 2 | + {(b - 5)}^{2} = 0$ ， c为奇数，则c=.

查看试题解析
13. 已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形有个．

查看试题解析
14. 用材质规格相同的火柴棒搭一个三角形，现用24根火柴棒搭一个三角形（全部用完），则一共可搭个形状不同的三角形．

查看试题解析
15. 如图所示，三角形的两边长分别是4cm和6cm，则第三边长x的范围是

查看试题解析

三、解答题

16. 已知：a，b，c是三角形的三条边，化简： $| a - b - c | + | - a + b - c | + | a - c + b |$ ．

查看试题解析
17. 已知三角形三边长分别为a ， b ， c ，其中a ， b满足（a﹣8）²+|b﹣6|＝0，求这个三角形的第三边长c的取值范围．

查看试题解析
18. 一个三角形的三边长分别是xcm、（x+2）cm、（x+5）cm.它的周长不超过37cm.求x的取值范围.

查看试题解析
19. 在 $Δ A B C$ 中，已知 $A B = 3, A C = 7$ ，若第三边 $B C$ 的长为偶数，求 $Δ A B C$ 的周长.

查看试题解析

四、综合题

20. 若△ABC的三边长分别为m－2，2m＋1，8．

(1)、求m的取值范围；

(2)、若△ABC的三边均为整数，求△ABC的周长．

查看试题解析
21. 如图

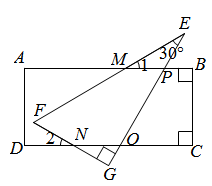(1)、如图所示，直角三角板和直尺如图放置．若 $∠ 1 = 20 °$ ，试求出 $∠ 2$ 的度数．

(2)、已知 $△$ ABC的三边长a、b、c，化简 $| a + b - c | - | b - a - c |$ ．

查看试题解析
22. “佳园工艺店”打算制作一批有两边长分别是7分米，3分米，第三边长为奇数（单位：分米）的不同规格的三角形木框．

(1)、要制作满足上述条件的三角形木框共有种．

(2)、若每种规格的三角形木框只制作一个，制作这种木框的木条的售价为8元╱分米，问至少需要多少钱购买材料？（忽略接头）

查看试题解析
23. 已知 △ABC 的周长为 37cm ， AD 是 BC 边上的中线， $A C = \frac{2}{3} A B$ ．

(1)、如图，当AB=15cm 时，求 BD 的长．

(2)、若 $A C = 14 c m$ ，能否求出 $D C$ 的长？为什么？

查看试题解析

（人教版）吉林地区七年级升八年级2023年暑假衔接 专题1 三角形的边

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）吉林地区七年级升八年级2023年暑假衔接专题1 三角形的边