2023年高考物理全国甲卷真题变式·分层精准练：第12题

试卷更新日期：2023-06-13 类型：二轮复习

进入出卷网下载

一、原题

1. 如图，水平桌面上固定一光滑U型金属导轨，其平行部分的间距为1，导轨的最右端与桌子右边缘对齐，导轨的电阻忽略不计。导轨所在区域有方向竖直向上的匀强磁场，磁感应强度大小为B。一质量为m、电阻为R、长度也为l的金属棒P静止在导轨上。导轨上质量为3m的绝缘棒Q位于P的左侧，以大小为v₀的速度向P运动并与P发生弹性碰撞，碰撞时间很短。碰撞一次后，P和Q先后从导轨的最右端滑出导轨，并落在地面上同一地点。P在导轨上运动时，两端与导轨接触良好，P与Q始终平行。不计空气阻力。求

(1)、金属棒P滑出导轨时的速度大小；

(2)、金属体P在导轨上运动过程中产生的热量；

(3)、与P碰撞后，绝缘棒Q在导轨上运动的时间。

查看试题解析

二、基础

2. 据报道，海南琼中法院审结了一起高空抛物致人身体损害案件，七旬老人纪某被盒装牛奶砸伤，9岁男童高空抛物，其家属被判赔偿7万余元。城市进入高楼时代后，高空坠物已成为危害极大的社会安全问题。小张同学想用所学的物理知识来作检验，他建立了如下的情景：如图，250mL牛奶的质量为300g，高度为10cm，设想从18楼（离地45m高）由静止开始释放，直立落地后高度减为原来的一半时速度变为0，此过程把牛奶顶端的运动处理为匀减速运动并作为撞击地面的时间。不计空气阻力，g取10m/s²。帮小张同学求：

(1)、牛奶落地时的速度大小；

(2)、牛奶在撞击地面过程中对地面的平均冲击力大小。

查看试题解析
3. 2022年，球王梅西率阿根廷队获得卡塔尔世界杯冠军，捧起了大力神杯。图中球王梅西练习用头颠球的场景。某一次足球由静止下落到头顶的速度大小 $v_{1} = 3 m/s$ ，被重新竖直向上顶起离开头顶时的速度大小 $v_{2} = 4 m/s$ 。已知足球与头部的作用时间为 $0.1 s$ ，足球的质量为 $0.6 k g$ ，空气阻力不计，重力加速度 $g$ 取 ${10m/s}^{2}$ ，在足球与头顶相互作用的过程中，求：

(1)、足球的动量变化量的大小；

(2)、头顶受到足球的平均作用力的大小。

查看试题解析
4. 短道速滑接力赛是北京冬奥会上极具观赏性的比赛项目之一，如图所示为A、B两选手在比赛中的某次交接棒过程。A的质量 $m_{A} = 60 k g$ ， B的质量 $m_{B} = 75 k g$ ，交接开始时A在前接棒，B在后交棒，交棒前两人均以 $v_{0} = 10 m / s$ 的速度向前滑行。交棒时B从后面用力推A，当两人分开时B的速度变为 $v_{1} = 6 m / s$ ，方向仍然向前，不计两人所受冰面的摩擦力，且交接棒前后瞬间两人均在一条直线上运动。

(1)、求两人分开时A的速度大小；

(2)、交接棒过程要消耗B体内的生物能，设这些能量全部转化为两人的动能，且不计其它力做功，求B消耗的生物能E。

查看试题解析
5. 某地有一风力发电机，它的叶片转动时可形成半径为 $R$ 的圆面。某时间内该地区的风速恒定为 $v_{0}$ ，风向恰好跟叶片转动的圆面垂直，已知空气的密度为 $ρ$ ，假设这个风力发电机能将此圆面内10%的空气动能转化为电能。求：

(1)、单位时间内冲击风力发电机叶片圆面的气流的动能；

(2)、此风力发电机的发电功率。

查看试题解析
6. 如图所示为某公园的大型滑梯，滑梯长度L=9m，滑梯平面与水平面夹角θ=37°，滑梯底端与水平面平滑连接。某同学从滑梯顶端由静止滑下，与倾斜接触面间的动摩擦因数μ₁=0.5，与水平接触面之间的动摩擦因数μ₂=0.6。已知sin37°=0.6，cos37°=0.8，g=10m/s² ，求：

(1)、该同学在斜面上下滑时的加速度大小；

(2)、该同学滑到斜面底端时的速度大小；

(3)、该同学在水平面上滑行的距离。

查看试题解析

三、巩固

7. 如图所示为某精密电子器件防撞装置，电子器件T和滑轨PQNM固定在一起，总质量为 $m_{1}$ ，滑轨内置磁场的磁感应强度为B。受撞滑块K套在PQ，MN滑轨内，滑块K上嵌有闭合线圈abcd，线圈abcd总电阻为R，匝数为n，bc边长为L，滑块K（含线圈）质量为 $m_{2}$ ，设T、K一起在光滑水平面上以速度 $v_{0}$ 向左运动，K与质量为 $m_{3}$ 的静止障碍物C相撞后结为一体后继续运动。不计滑块与滑轨间的摩擦作用，ab大于滑轨长度。

(1)、求滑块K与C碰撞后瞬间速度大小和bc边受到的最大安培力；

(2)、设滑轨足够长，防撞装置和障碍物C所吸收的总机械能；

(3)、为使保险杠线圈bc边不与器件T发生直接碰撞，求滑轨的长度满足的条件。

查看试题解析
8. 2023年1月15日，长征二号丁运载火箭以“一箭十四星”发射方式成功将齐鲁二号、三号等14颗卫星发射升空。已知火箭的总质量 $m = 2.5 \times 1 0^{5} k g$ ，火箭发动机点火后从尾部竖直向下喷出高温高压气体而获得动力。火箭尾部喷口横截面积 $S = 0.75 m^{2}$ ，喷出气体的密度 $ρ = 1 k g / m^{3}$ ，火箭点火瞬间竖直向下喷出气体相对地面的速度大小 $v = 2 \times 1 0^{3} m / s$ ，此后火箭向上做匀加速直线运动，取重力加速度大小 $g = 10 m / s^{2}$ ，不考虑火箭由于喷气带来的质量变化，忽略地球的自转以及高度的变化对重力加速度的影响，空气阻力不计。求：

(1)、点火瞬间，火箭因喷出气体获得的动力大小F；

(2)、从点火开始计时，火箭运行 $t = 10 s$ 过程中火箭动力所做的功W。

查看试题解析
9. 如图，L形滑板A静止在粗糙水平面上，在A上距离其左端为3l处静置小木块B，AB之间光滑；水平面上距离A右端处静止着一滑块C，A和C与水平面之间的动摩擦因数均为μ。ABC的质量均为m，AB、AC之间的碰撞都属于完全非弹性碰撞且不粘连。现对A施加水平向右的恒定推力，当AC相碰瞬间撤去，碰撞后瞬间AC的速度 $v_{A C} = 4 \sqrt{μ g l}$ ，由于A板足够长，所以不考虑BC的相碰。已知重力加速度为g。求：

(1)、水平推力F的大小；

(2)、当AC都停下时C离A板右端的距离d。

查看试题解析
10. 如图所示，一对平行的光滑金属导轨固定在同一水平面内，导轨间距L=0.5m，左端接有阻值 $R = 0.3 Ω$ 的电阻。一质量m=0.2kg、电阻 $r = 0.1 Ω$ 的金属棒MN放置在导轨上，整个装置置于竖直向上的匀强磁场中，磁场的磁感应强度大小B=0.4T。棒在水平向右的拉力F作用下，由静止开始以 $a = 2 {m/s}^{2}$ 的加速度做匀加速直线运动。当棒的位移x=9m时撤去力F，棒继续运动一段距离后静止。若导轨足够长且电阻不计，棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求：

(1)、力F撤去前其大小随时间变化的关系；

(2)、撤去力F后电阻R上产生的焦耳热Q；

(3)、撤去力F后金属棒MN继续向前运动的距离。

查看试题解析

四、提升

11. 如图，水平面中间夹有一水平传送带，水平面与传送带上表面平齐且平滑连接，左侧水平面上c点左侧部分粗糙，右侧部分光滑，传送带右侧水平面光滑。质量为 $m_{1} = 2 k g$ 的小滑块P与固定挡板间有一根劲度系数为k=29.12N/m的轻弹簧（P与弹簧不拴接），初始时P放置在c点静止且弹簧处于原长。传送带初始静止，在传送带左端点a处停放有一质量为 $m_{2} = 1 k g$ 的小滑块Q。现给P施加一水平向左、大小为F=20.2N的恒力，使P向左运动，当P速度为零时立即撤掉恒力，一段时间后P将与Q发生弹性碰撞（不计碰撞时间），以后P、Q间的碰撞都是弹性碰撞，在P、Q第一次碰撞时传送带由静止开始做顺时针方向的匀加速运动，加速度大小为 $a_{1} = 1 m / s^{2}$ ，当速度达到v=4m/s时传送带立即做匀减速运动直至速度减为零，加速度大小为 $a_{2} = 2 m / s^{2}$ ，当传送带速度减为零时，Q恰好运动到传送带右端点b处。已知P与水平面、传送带间的动摩擦因数均为 $μ_{1} = 0.1$ ， Q与传送带间的动摩擦因数 $μ_{2} = 0.3$ ，最大静摩擦力等于滑动摩擦力，弹簧的形变在弹性限度内，弹簧的弹性势能表达式为 $E_{p} = \frac{1}{2} k x^{2}$ ， x为弹簧的形变量，重力加速度g取 $10 m / s^{2}$ ，不计空气阻力。求：

(1)、P与Q第一次碰前P的速度大小；

(2)、为保证P与Q能够相碰，求恒力的最小值；

(3)、P、Q最终的速度大小；

(4)、P、Q由于与传送带间的摩擦，系统产生的热量。

查看试题解析
12. 竖直面内的水平轨道上有一半径为 $R = 1.5 m$ 、圆心角为 $θ = 60 °$ 的固定光滑圆弧轨道，其底端紧靠一质量为 $M = 0.2 kg$ 的长木板，长木板上表面与圆弧轨道底端平齐，长木板右端放置一小物块P，如图甲所示。用足够长轻绳拴接的两个小滑块A、B分别置于圆弧轨道两侧，A刚好被锁定在圆弧轨道上端，B悬停在空中。现解除锁定，A下滑至圆弧轨道底端时与P发生弹性碰撞（碰撞时间极短），碰撞后，A立即又被锁定，P开始运动的v-t图像如图乙所示，图中的 $v_{0}$ 、 $t_{0}$ 、 $t_{1}$ 均为未知量，整个运动过程中P始终未滑离长木板。已知A的质量为 $m_{0} = 1.2 kg$ ， B、P的质量均为 $m = 0.4 kg$ ， P与长木板之间的动摩擦因数为 $μ_{1} = 0.5$ ，长木板与水平轨道之间的动摩擦因数为 $μ_{2} = 0.3$ ， P、A、B均可视为质点，重力加速度大小为 $g = 10 {m/s}^{2}$ 。求

(1)、 $v_{0}$ 、 $t_{0}$ 的值；

(2)、 $0 ~ t_{0}$ 与 $t_{0} ~ t_{1}$ 过程，小物块P、长木板和水平轨道组成的系统因摩擦产生内能的比值。

查看试题解析
13. 如图所示，表面水平的小车B静止在光滑水平面上，小物块A（可视为质点）以初速度v从小车左端水平滑上小车，此后当A、B恰好共速时，B与正前方静置在墙内水平均匀孔道中的细杆C发生碰撞。已知：A、B、C的质量为m，所有的碰撞均为弹性碰撞，碰撞时间极短可忽略不计，A、B间和C与墙内孔道间的滑动摩擦力大小均为 $k m g$ ，重力加速度为g，小车表面及墙内孔道均足够长。不计空气阻力，则：

(1)、求B、C的起始间距；

(2)、若B、C可以发生二次碰撞，求第一次碰撞后到第二次碰撞前的过程中，B匀速运动的位移和C所运动的位移；

(3)、若B、C只能发生二次碰撞，求细杆原来裸露在墙外的长度满足的条件。

查看试题解析
14. 一游乐设施简化模型如图所示，挡板1、2分别固定在光滑斜面的顶端和底端，相距为L，A为一小滑块，B为不计质量的板（在外力的作用下可以瞬间获得或失去速度），长度 $\frac{L}{2}$ ， AB间的滑动摩擦力大小恒等于A的重力，A、B与挡板的碰撞都是弹性碰撞，已知斜面的倾角 $θ = 30 °$ ，重力加速度为g。

(1)、若将置于板上端的滑块A以初速度为零释放，求滑块A到达挡板2时的速度大小。

(2)、在挡板1处有发射装置，可以将置于板上端的滑块A沿平行于斜面的方向发向发射，要使滑块A恰能回到挡板1处，求滑块A需要的发射速度大小。

(3)、在（2）中，若使滑块A以初速度 $v = \sqrt{g L}$ 发射，求滑块A做周期性运动时的周期。

查看试题解析
15. 如图所示，质量 $m_{1} = 1 k g$ 的长木板静置于光滑水平面上，木板左端有挡板，水平轻弹簧左端固定于挡板上，质量 $m_{2} = 1 k g$ 可视为质点的小物块置于木板右端，物块与弹簧右端相距 $L = 1 m$ 。现给物块一大小 $I = 4 N \cdot s$ 、方向水平向左的瞬时冲量，物块向左运动，与弹簧发生作用后，距木板右端 $d = 0.6 m$ 处相对木板静止。已知物块与木板间的动摩擦因数 $μ = 0.25$ ，弹簧始终处于弹性限度内，重力加速度大小g取10 $m / s^{2}$ 。求：

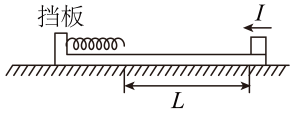(1)、物块刚获得冲量后的速度大小v；

(2)、系统在整个过程中产生的热量Q；

(3)、弹簧具有的弹性势能的最大值 $E_{p m}$ 。

查看试题解析
16. 有一质量 $m = 1 k g$ 的长木板静止在光滑水平面上，某时刻A、B两个可视为质点的滑块同时从左右两端滑上木板，两个滑块的初始速度大小相等且 $v_{0} = 4 m / s$ ，两个滑块刚好没有相碰。已知两个滑块与木板的动摩擦因数 $μ = 0.5$ ，两个滑块的质量 $m_{A} = 2 m_{B} = 2 k g$ ，当地重力加速度 $g = 10 m / s^{2}$ 。求：

(1)、滑块A最后的速度；

(2)、此过程中系统产生的热量；

(3)、木板的长度。

查看试题解析