【高考真题】2023年普通高等学校招生全国统一考试(天津卷)数学

试卷更新日期：2023-06-12 类型：高考真卷

进入出卷网下载

一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 已知集合 $U = {1 ， 2 ， 3 ， 4 ， 5} ， A = {1 ， 3} ， B = {1 ， 2 ， 4}$ ，则 $∁_{U} B ∪ A =$ （）

A、 ${1 ， 3 ， 5}$ B、 ${1 ， 3}$ C、 ${1 ， 2 ， 4}$ D、 ${1 ， 2 ， 4 ， 5}$

查看试题解析
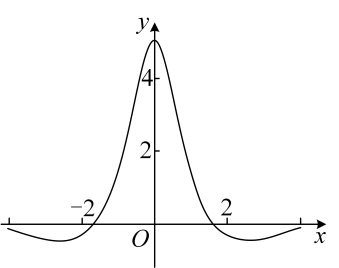
2. “ $a^{2} = b^{2}$ ”是“ $a^{2} + b^{2} = 2 a b$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分又不必要条件

查看试题解析
3. 若 $a = 1.0 1^{0.5} ， b = 1.0 1^{0.6} ， c = 0 . 6^{0.5}$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $c > a > b$ B、 $c > b > a$ C、 $a > b > c$ D、 $b > a > c$

查看试题解析
4. 函数 $f (x)$ 的图象如下图所示，则 $f (x)$ 的解析式可能为（）

A、 $\frac{5 (e^{x} - e^{- x})}{x^{2} + 2}$ B、 $\frac{5 s i n x}{x^{2} + 1}$ C、 $\frac{5 (e^{x} + e^{- x})}{x^{2} + 2}$ D、 $\frac{5 c o s x}{x^{2} + 1}$

查看试题解析
5. 已知函数 $f (x)$ 的一条对称轴为直线 $x = 2$ ，一个周期为4，则 $f (x)$ 的解析式可能为（）

A、 $s i n (\frac{π}{2} x)$ B、 $c o s (\frac{π}{2} x)$ C、 $s i n (\frac{π}{4} x)$ D、 $c o s (\frac{π}{4} x)$

查看试题解析
6. 已知 ${a_{n}}$ 为等比数列， $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和， $a_{n + 1} = 2 S_{n} + 2$ ，则 $a_{4}$ 的值为（）

A、3 B、18 C、54 D、152

查看试题解析
7. 调查某种群花萼长度和花瓣长度，所得数据如图所示，其中相关系数 $r = 0.8245$ ，下列说法正确的是（）

A、花瓣长度和花萼长度没有相关性 B、花瓣长度和花萼长度呈现负相关 C、花瓣长度和花萼长度呈现正相关 D、若从样本中抽取一部分，则这部分的相关系数一定是 $0.8245$

查看试题解析
8. 在三棱锥 $P - A B C$ 中，线段 $P C$ 上的点 $M$ 满足 $P M = \frac{1}{3} P C$ ，线段 $P B$ 上的点 $N$ 满足 $P N = \frac{2}{3} P B$ ，则三棱锥 $P - A M N$ 和三棱锥 $P - A B C$ 的体积之比为（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看试题解析
9. 双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} 、 F_{2}$ ．过 $F_{2}$ 作其中一条渐近线的垂线，垂足为 $P$ ．已知 $P F_{2} = 2$ ，直线 $P F_{1}$ 的斜率为 $\frac{\sqrt{2}}{4}$ ，则双曲线的方程为（）

A、 $\frac{x^{2}}{8} - \frac{y^{2}}{4} = 1$ B、 $\frac{x^{2}}{4} - \frac{y^{2}}{8} = 1$ C、 $\frac{x^{2}}{4} - \frac{y^{2}}{2} = 1$ D、 $\frac{x^{2}}{2} - \frac{y^{2}}{4} = 1$

查看试题解析

二、填空题：本大题共6小题，每小题5分，共30分．试题中包含两个空的，答对1个的给3分，全部答对的给5分．

10. 已知 $i$ 是虚数单位，化简 $\frac{5 + 14 i}{2 + 3 i}$ 的结果为．

查看试题解析
11. 在 ${(2 x^{3} - \frac{1}{x})}^{6}$ 的展开式中， $x^{2}$ 项的系数为．

查看试题解析
12. 过原点的一条直线与圆 $C ： (x + 2)^{2} + y^{2} = 3$ 相切，交曲线 $y^{2} = 2 p x (p > 0)$ 于点 $P$ ，若 $| O P | = 8$ ，则 $p$ 的值为．

查看试题解析
13. 甲乙丙三个盒子中装有一定数量的黑球和白球，其总数之比为 $5 ： 4 ： 6$ ．这三个盒子中黑球占总数的比例分别为 $40 % ， 25 % ， 50 %$ ．现从三个盒子中各取一个球，取到的三个球都是黑球的概率为；将三个盒子混合后任取一个球，是白球的概率为．

查看试题解析
14. 在 $△ A B C$ 中， $∠ A = 6 0^{∘}$ ， $B C = 1$ ，点 $D$ 为 $A B$ 的中点，点 $E$ 为 $C D$ 的中点，若设 $\vec{A B} = \vec{a} ， \vec{A C} = \vec{b}$ ，则 $\vec{A E}$ 可用 $\vec{a} ， \vec{b}$ 表示为；若 $\vec{B F} = \frac{1}{3} \vec{B C}$ ，则 $\vec{A E} \cdot \vec{A F}$ 的最大值为．

查看试题解析
15. 若函数 $f (x) = a x^{2} - 2 x - | x^{2} - a x + 1 |$ 有且仅有两个零点，则 $a$ 的取值范围为．

查看试题解析

三、解答题：本大题共5小题，共75分，解答应写出文字说明，证明过程或演算步骤．

16. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分別是 $a ， b ， c$ ．已知 $a = \sqrt{39} ， b = 2 ， ∠ A = 12 0^{∘}$ ．

(1)、求 $s i n B$ 的值；

(2)、求 $c$ 的值；

(3)、求 $s i n (B - C)$ ．

查看试题解析
17. 三棱台 $A B C - A_{1} B_{1} C_{1}$ 中，若 $A_{1} A ⊥$ 面 $A B C ， A B ⊥ A C ， A B = A C = A A_{1} = 2 ， A_{1} C_{1} = 1$ ， $M ， N$ 分别是 $B C ， B A$ 中点.

(1)、求证： $A_{1} N$ //平面 $C_{1} M A$ ；

(2)、求平面 $C_{1} M A$ 与平面 $A C C_{1} A_{1}$ 所成夹角的余弦值；

(3)、求点 $C$ 到平面 $C_{1} M A$ 的距离．

查看试题解析
18. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右顶点分别为 $A_{1} ， A_{2}$ ，右焦点为 $F$ ，已知 $| A_{1} F | = 3 ， | A_{2} F | = 1$ ．

(1)、求椭圆方程及其离心率；

(2)、已知点 $P$ 是椭圆上一动点（不与端点重合），直线 $A_{2} P$ 交 $y$ 轴于点 $Q$ ，若三角形 $A_{1} P Q$ 的面积是三角形 $A_{2} F P$ 面积的二倍，求直线 $A_{2} P$ 的方程．

查看试题解析
19. 已知 ${a_{n}}$ 为等差数列， $a_{2} + a_{5} = 16 ， a_{5} - a_{3} = 4$ ．

(1)、求 ${a_{n}}$ 的通项公式和 $\sum_{i = 2^{n - 1}}^{2^{n} - 1} a_{i}$ ．

(2)、已知 ${b_{n}}$ 为等比数列，对于任意 $k \in N^{*}$ ，若 $2^{k - 1} \leq n \leq 2^{k} - 1$ ，则 $b_{k} < a_{n} < b_{k + 1}$ ，
（Ⅰ）当 $k \geq 2$ 时，求证： $2^{k} - 1 < b_{k} < 2^{k} + 1$ ；

（Ⅱ）求 ${b_{n}}$ 的通项公式及其前 $n$ 项和．

查看试题解析
20. 已知函数 $f (x) = (\frac{1}{x} + \frac{1}{2}) l n (x + 1)$ ．

(1)、求曲线 $y = f (x)$ 在 $x = 2$ 处切线的斜率；

(2)、当 $x > 0$ 时，证明： $f (x) > 1$ ；

(3)、证明： $\frac{5}{6} < l n (n!) - (n + \frac{1}{2}) l n (n) + n \leq 1$ ．

查看试题解析