鲁教版(五四学制) 2022-2023学年六年级数学下册 第九章 变量之间的关系 单元测试
试卷更新日期:2023-06-12 类型:单元试卷
一、单选题
-
1. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/
-20
-10
0
10
20
30
声速/
318
324
330
336
342
348
下列说法错误的是( )
A、在这个变化中,自变量是温度,因变量是声速 B、温度越高,声速越快 C、当空气温度为时,声速为 D、当温度每升高 , 声速增加2. 周一,小南爸爸开车送小南去上学,匀速行驶了一段后,遇上了早高峰,停滞不前,之后为了不迟到,立即以较快的速度匀速到达学校.在小南爸爸开车送小南过程中x表示小南爸爸开车的时间,y表示他们离学校的距离,下面能反映y与x的关系的大致图像是( )A、 B、
B、 C、
C、 D、
D、 3. 下列各情景分别可以用哪一幅图来近似的刻画?正确的顺序是( )
3. 下列各情景分别可以用哪一幅图来近似的刻画?正确的顺序是( )①汽车紧急刹车(速度与时间的关系)
②人的身高变化(身高与年龄的关系)
③跳过运动员跳跃横杆(高度与时间的关系)
④一面冉冉上升的红旗(高度与时间的关系) A、 B、 C、 D、4. 山西某煤矿一个水池存有1000L水,现在水泵以每分钟抽水20L的速度把水池的水抽出,下图能近似的表示水池剩余水量y与抽水时间x的关系的是( )A、
A、 B、 C、 D、4. 山西某煤矿一个水池存有1000L水,现在水泵以每分钟抽水20L的速度把水池的水抽出,下图能近似的表示水池剩余水量y与抽水时间x的关系的是( )A、 B、
B、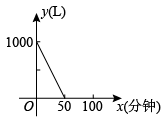 C、
C、 D、
D、 5. 某天学校组织学生到市文化宫参观学习,早上,大客车从学校出发到市文化宫,匀速行驶一段时间后,途中遇到堵车,原地等了一会,然后大客车加快速度行驶,按时到达文化宫参观学习后,大客车匀速行驶返回.其中t表示客车从学校出发后所用的时间,s表示客车离学校的距离.下面能反映s与t的函数关系的大致图象是( )A、
5. 某天学校组织学生到市文化宫参观学习,早上,大客车从学校出发到市文化宫,匀速行驶一段时间后,途中遇到堵车,原地等了一会,然后大客车加快速度行驶,按时到达文化宫参观学习后,大客车匀速行驶返回.其中t表示客车从学校出发后所用的时间,s表示客车离学校的距离.下面能反映s与t的函数关系的大致图象是( )A、 B、
B、 C、
C、 D、
D、 6. 某施工队修一段长度为360米的公路,施工队每天的效率相同,如表根据每天工程进度制作而成的.
6. 某施工队修一段长度为360米的公路,施工队每天的效率相同,如表根据每天工程进度制作而成的.施工时间/天
1
2
3
4
5
6
7
……
累计完成施工量/米
30
60
90
120
150
180
210
……
下列说法错误的是( )
A、随着施工时间的逐渐增大,累计完成施工量也逐渐增大 B、施工时间每增加1天,累计完成施工量就增加30米 C、当施工时间为9天时,累计完成施工量为270米 D、若累计完成施工量为330米,则施工时间为10天7. 若x=2m+1,y=4m﹣3,则下列x,y关系式成立的是( )A、y=(x﹣1)2﹣4 B、y=x2﹣4 C、y=2(x﹣1)﹣3 D、y=(x﹣1)2﹣38. 瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )层数n/层
1
2
3
4
5
……
物体总数y/个
1
3
6
10
15
……
 A、在这个变化过程中层数是自变量,物体总数是因变量 B、当堆放层数为7层时,物体总数为28个 C、物体的总数随着层数的增加而均匀增加 D、物体的总数y与层数n之间的关系式为
A、在这个变化过程中层数是自变量,物体总数是因变量 B、当堆放层数为7层时,物体总数为28个 C、物体的总数随着层数的增加而均匀增加 D、物体的总数y与层数n之间的关系式为二、填空题
-
9. 某复印店用电脑编辑并打印一张文稿收费2元,再每复印一张收费0.3元,则总收费y(元)与同样文稿的数量x(张)之间的关系式是 .10. 小红用一根长为60cm的铁丝围成一个长方形,若一边长为 , 相邻的另一边长为 , 则与的关系为 .11. 某汽车生产厂对其生产的型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量(升)与行驶时间(小时)之间的关系如下表:
(小时)
0
1
2
3
(升)
100
92
84
76
由表格中与的关系可知,当汽车行驶小时,油箱的余油量为40升.
12. 如图,正方形边长为12cm,在四个角分别剪去全等的等腰直角三角形.当三角形的直角边由小变大时,阴影部分的面积变化如下表所示:三角形的直角边/cm
1
2
3
4
5
6
阴影部分的面积
142
136
126
112
94
72
若等腰直角三角形的直角边长为3cm,则图中阴影部分的面积是 .

三、解答题
-
13.
下表给出了橘农王林去年橘子的销售额(元)随橘子卖出质量(千克)的变化的有关数据:

(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是多少?
(3)估计当橘子卖出50千克时,销售额是多少?
14. 分析并指出下列关系中的变量与常量:(1)球的表面积S cm2与球的半径R cm的关系式是S=4πR2;
(2)以固定的速度v0米/秒向上抛一个小球,小球的高度h米与小球运动的时间t秒之间的关系式是h=v0t﹣4.9t2;
(3)一物体自高处自由落下,这个物体运动的距离h m与它下落的时间t s的关系式是h=gt2(其中g取9.8m/s2);
(4)已知橙子每千克的售价是1.8元,则购买数量W千克与所付款x元之间的关系式是x=1.8W.
四、综合题
-
15. 根据心理学家研究发现,学生对一个新概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系(其中0≤x≤30)
提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)、上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、根据表格中的数据,提出概念所用时间是多少时,学生的接受能力最强?(3)、学生对一个新概念的接受能力在什么时间段内逐渐增强?在什么时间段内逐渐减弱?16. 下表是某商行某商品的销售情况,该商品原价为600元,随着不同幅度的降价(单位:元),日销量(单位:件)发生相应变化如下:降价(元)
5
10
15
20
25
30
35
日销量(件)
780
810
840
870
900
930
960
(1)、上表反映了哪两个变量之间的关系?哪个是自变量,哪个是因变量?(2)、每降价5元,日销量增加多少件?降价之前的日销量是多少?(3)、如果售价为540元时,日销量为多少?