鲁教版(五四学制) 2022-2023学年六年级数学下册 第七章 平行线与相交线 单元测试
试卷更新日期:2023-06-12 类型:单元试卷
一、单选题
-
1. 如图,当剪刀口减小时,的度数( )
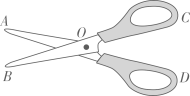 A、增大 B、不变 C、减小 D、减小2. 下列说法不正确的是( )A、两直线被第三条直线所截,所得的同位角相等 B、两平行线被第三条直线所截,一组内错角的角平分线互相平行 C、两平行线被第三条直线所截,一组同位角的角平分线互相平行 D、两平行线被第三条直线所截,一组同旁内角的角平分线互相垂直3. 如图,直线直线 , 在中, , 顶点A在上,顶点B在上,且平分 . 若 , 求的度数.下面是嘉琪在作业本上写出的解答过程,他故意把部分步骤内容用小图标遮挡.
A、增大 B、不变 C、减小 D、减小2. 下列说法不正确的是( )A、两直线被第三条直线所截,所得的同位角相等 B、两平行线被第三条直线所截,一组内错角的角平分线互相平行 C、两平行线被第三条直线所截,一组同位角的角平分线互相平行 D、两平行线被第三条直线所截,一组同旁内角的角平分线互相垂直3. 如图,直线直线 , 在中, , 顶点A在上,顶点B在上,且平分 . 若 , 求的度数.下面是嘉琪在作业本上写出的解答过程,他故意把部分步骤内容用小图标遮挡.
关于小图标遮挡的内容,下面的回答错误的是( )
 A、
A、 代表
B、
代表
B、 代表
C、
代表
C、 代表
D、
代表
D、 代表
4. 如图,下列条件中,不能判断AB∥CD的是 ( )
代表
4. 如图,下列条件中,不能判断AB∥CD的是 ( )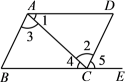 A、∠3=∠2 B、∠1=∠4 C、∠B=∠5 D、∠D+∠BAD=180°5. 下列命题:①相等的角是对顶角;②互补的角就是邻补角;③两条直线被第三条直线所截,同位角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直;⑤邻补角的平分线互相垂直,其中真命题的个数为( )A、0个 B、1个 C、2个 D、3个6. 如图,相交于点O, , , 有如下四个结论:
A、∠3=∠2 B、∠1=∠4 C、∠B=∠5 D、∠D+∠BAD=180°5. 下列命题:①相等的角是对顶角;②互补的角就是邻补角;③两条直线被第三条直线所截,同位角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直;⑤邻补角的平分线互相垂直,其中真命题的个数为( )A、0个 B、1个 C、2个 D、3个6. 如图,相交于点O, , , 有如下四个结论:①;②;③;④ .
上面结论中,所有正确结论的序号是( )
 A、①② B、①②④ C、①②③ D、①②③④7. 如图,已知 , 小华把三角板的直角顶点放在直线上,若 , 则的度数为( )
A、①② B、①②④ C、①②③ D、①②③④7. 如图,已知 , 小华把三角板的直角顶点放在直线上,若 , 则的度数为( )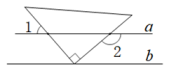 A、131 B、121 C、139 D、1298. 在同一平面内,已知 , 若直线、之间的距离为 , 直线、之间的距离为 , 则直线、间的距离为( )A、或 B、 C、 D、不确定9. 如图, , , 平分 , 平分 , 则( )
A、131 B、121 C、139 D、1298. 在同一平面内,已知 , 若直线、之间的距离为 , 直线、之间的距离为 , 则直线、间的距离为( )A、或 B、 C、 D、不确定9. 如图, , , 平分 , 平分 , 则( )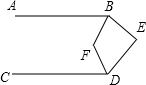 A、 B、 C、 D、10. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A、 B、 C、 D、10. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.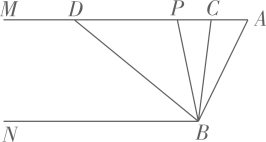 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,点C在射线上,只需添加一个条件即可证明 , 这个条件可以是(写出一个即可).
 12. 如图, , 直线平分 , 则 .
12. 如图, , 直线平分 , 则 .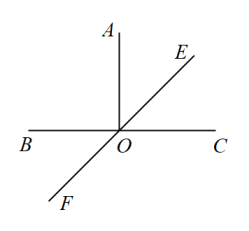 13. 如图,直线m与∠AOB的一边射线OB相交,∠3=120°,向上平移直线m得到直线n,与∠AOB的另一边射线OA相交,则∠2-∠1=°.
13. 如图,直线m与∠AOB的一边射线OB相交,∠3=120°,向上平移直线m得到直线n,与∠AOB的另一边射线OA相交,则∠2-∠1=°.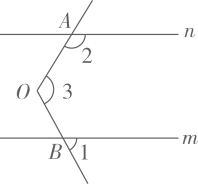 14. 如图,直线AB∥CD,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分∠CEF,则∠1的度数为 °.
14. 如图,直线AB∥CD,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分∠CEF,则∠1的度数为 °.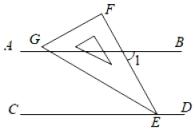 15. 如图,已知 , 、分别在、上,点在、之间,连接、 , , 平分 , 平分 , 在的下方有一点 , 平分 , 平分 , 求的度数为 .
15. 如图,已知 , 、分别在、上,点在、之间,连接、 , , 平分 , 平分 , 在的下方有一点 , 平分 , 平分 , 求的度数为 .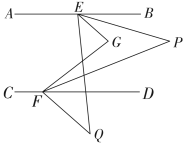
三、作图题
-
16. 已知: , 线段b.
求作: , 使 , , .

四、解答题
-
17. 已知:如图,AD∥BC,AE是∠BAD的角平分线,AE交CD于点F,交BC的延长线于点E,且∠E=∠CFE,请说明∠ABF=∠BFC的理由.
 18. 已知:如图 , , 度,度,求∠C的度数.
18. 已知:如图 , , 度,度,求∠C的度数.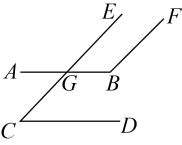
五、综合题
-
19. 【概念认识】
两条直线相交所形成的锐角或直角称为这两条直线的夹角,如果两条直线的夹角为α,那么我们称这两条直线是“α相交线”例如;如图①,直线m和直线n为“α相交线”我们已经知道两条平行线被第三条直线所截,同位角相等、内错角相等、同旁内角互补,那么若两条直线为“α相交线”,它们被第三条直线所截后形成的同位角、内错角、同旁内角之间有什么关系呢?
(1)、【初步研究】如图②,直线m与直线n是“α相交线”,求证:
小明的证法如图③.若直线m与直线n交于点O,
直线m与直线n是“α相交线”.
∵ .
∴是的外角,
∴ .
即 .
请补充完整小明的证明过程,并用另一种不同的方法进行证明
 (2)、【深入思考】
(2)、【深入思考】如图④,直线m与直线n是α相交线,
①找出直线m与直线n被直线l所截得的内错角,并直接写出内错角与α的关系;
②找出直线m与直线n被直线l所截得的同旁内角,并直接写出每对同旁内角与α的关系;
 (3)、【综合运用】
(3)、【综合运用】如图⑤,已知∠α,用直尺和圆规按下列要求作图,
如图⑥,直线外求作一点M,使得直线与直线是“α相交线”(不写作图过程,保留作图痕迹).
 20. 如图,线段交线段 , 于点H,G,已知 , ,
20. 如图,线段交线段 , 于点H,G,已知 , ,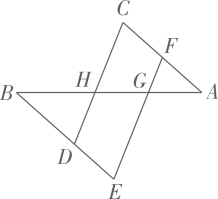 (1)、求证: .(2)、若 , 求证: .(3)、在(2)的条件下,若 , 求的度数.
(1)、求证: .(2)、若 , 求证: .(3)、在(2)的条件下,若 , 求的度数.
-