鲁教版(五四学制) 2022-2023学年六年级数学下册 6.8 整式的除法同步测试

试卷更新日期：2023-06-11 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，用含m，n的代数式表示阴影部分的周长为（）

A、 $10 m + 10 n$ B、 $8 m + 10 n$ C、 $10 m + 22 n$ D、 $8 m + 22 n$

查看试题解析
2. 夏夏在检查作业时，发现有一道题的部分内容被墨水侵染了， $\times \frac{2}{3} a b = 2 a^{2} b^{3} + \frac{1}{3} a^{3} b^{2}$ ，那么这部分内容可能是（）

A、 $(3 a b^{2} + 2 a^{2} b)$ B、 $(3 a^{2} b + \frac{1}{2} a b^{2})$ C、 $(3 a b^{2} + \frac{1}{2} a^{2} b)$ D、 $(\frac{1}{3} a^{2} b^{2} + \frac{1}{2} a^{2} b)$

查看试题解析
3. 下列运算正确的是（）

A、 $3 a^{2} + 4 a^{2} = 7 a^{4}$ B、 ${(3 a^{2})}^{2} \div 4 a^{2} = \frac{3}{4} a^{2}$ C、 $3 a \cdot 4 a^{2} = 12 a^{2}$ D、 $3 a^{2} - 4 a^{2} = - a^{2}$

查看试题解析
4. 小双制作了如图所示的卡片A类，B类，C类各50张，其中A，B两类卡片都是正方形，C类卡片是长方形，现要拼一个长为(5a+7b)，宽为(7a+b)的大长方形，那么所准备的C类卡片的张数（）

A、够用，剩余4张 B、不够用，还缺4张 C、够用，剩余5张 D、不够用，还缺5张

查看试题解析
5. 设 $x$ ， $y$ 是实数，定义@的一种运算如下： $x$ @ $y = (x + y)^{2} - (x - y)^{2}$ ，则下列结论：①若 $x$ @ $y$ =0，则 $x = 0$ 或 $y = 0$ ；② $x$ @( $y$ +z)= $x$ @ $y$ + $x$ @z；③不存在实数 $x$ ， $y$ ，满足 $x$ @ $y = x^{2} + 5 y^{2}$ ；④设 $x$ ， $y$ 是矩形的长和宽，若矩形的周长固定，则当 $x = y$ 时， $x$ @ $y$ 最大，其中正确的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
6. 在矩形ABCD内，将两张边长分别为 a和b (a>b) 的正方形纸片按图1，图2两种方式放置(两张正方形纸片均有部分重叠) ，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S₁ ，图2中阴影部分的面积为S₂ ．当AD-AB=3时， S₂ -S₁的值是（）

A、3a B、3a-3b C、3b D、-3a

查看试题解析
7. 若定义表示xyz，表示 $4 a^{d} c^{b}$ ，则运算的结果为（）

A、 $2 m^{2} n$ B、 $4 m^{2} n$ C、 $2 m n^{2}$ D、 $4 m n^{2}$

查看试题解析

二、填空题

8. 若 $3 x + 5 y = 7$ ，用含有 $x$ 的代数式表示 $y$ ，则 $y =$

查看试题解析
9. 若一个多项式与 $- \frac{1}{2} m n$ 的乘积为 $3 m^{2} n - m n^{2} + \frac{1}{2} m n$ ，则这个多项式为．

查看试题解析
10. 一个长方形的面积为 $3 x^{2} + 2 x$ ，它的一条边长为x，则它的周长为．

查看试题解析
11. 定义一种新运算： a★b=ab-a² ，则x★(x+y)= ．

查看试题解析
12. 定义运算 $a * b = a b + a + b$ ，比如 $1 * 2 = 1 \times 2 + 1 + 2 = 5$ ， $1 * a = 1 \times a + 1 + a = 2 a + 1$ ，那么关于“ $*$ ”运算，以下等式成立的是 $. ① a * b = b * a$ ； $② (a + 1) * b = a * b + 1 * b$ ； $③ (a * b) * c = a * (b * c)$ ．

查看试题解析

三、计算题

13. 计算：

(1)、 $- x y^{2} z^{3} ﹒ {(- x^{2} y)}^{3}$

(2)、 $- 2 a^{2} (\frac{1}{2} a b + b^{2})$

(3)、 $[{(3 a + b)}^{2} - b^{2}] \div a$

(4)、 $[{(x + y)}^{2} - {(x - y)}^{2}] \div 2 x y$

查看试题解析

四、解答题

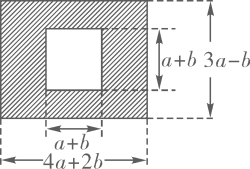
14. 眉山市三苏雕像广场是为了纪念三苏父子而修建的．原是一块长为(4a+2b)米，宽为(3a-b)米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为（a+b）米的正方形三苏父子雕像，则绿化的面积是多少平方米？并求出当a=20，b=10时的绿化面积．

查看试题解析
15. 菜单位为响应政府发出的全民健身的号召，打算在长宽分别为20米和11米的长方形大厅内修建一长方形健身房ABCD，该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为a元/m² ，比新建（含装修）墙壁的费用每平方米少50元，设健身房的高为3米，一面旧墙壁AB的长为x米，BC为 $(x - 5)$ 米，则修建健身房墙壁的总投入为多少元？（用含a、x的代数式表示）

查看试题解析

鲁教版(五四学制) 2022-2023学年六年级数学下册 6.8 整式的除法 同步测试

一、单选题

二、填空题

三、计算题

四、解答题

鲁教版(五四学制) 2022-2023学年六年级数学下册 6.8 整式的除法同步测试