人教版八年级下数学期末复习知识点扫盲满分计划——18.2.3正方形二
试卷更新日期:2023-06-11 类型:复习试卷
一、正方形性质与判定的证明
-
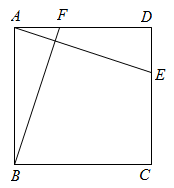
1. 已知:如图,在矩形ABCD中,E、F分别是边CD、AD上的点, , 且 . 求证:矩形ABCD是正方形.
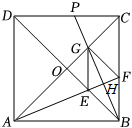
 2. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
2. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:. 3. 如图,是的垂直平分线,交于点M,过点M作 , 垂足分别为点E,F,已知 . 求证:四边形是正方形.
3. 如图,是的垂直平分线,交于点M,过点M作 , 垂足分别为点E,F,已知 . 求证:四边形是正方形.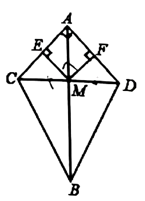 4. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .
4. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .求证:四边形是正方形.
 5. 如图,四边形ABCD和四边形CEFG都是正方形,连接BG、DE.求证:
5. 如图,四边形ABCD和四边形CEFG都是正方形,连接BG、DE.求证: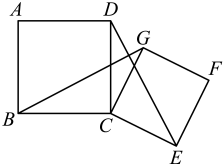 (1)、BG=DE;(2)、BG⊥DE.
(1)、BG=DE;(2)、BG⊥DE.二、(特殊)平行四边形的动点问题
-
6. 如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为xcm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
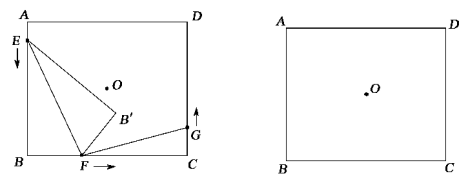 (1)、当t=s时,四边形EBFB'为正方形;(2)、当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?(3)、是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.7. 已知,如图:在直角坐标系中,正方形AOBC的边长为4,点D,E分别是线段AO,BO上的动点,D点由A点向O点运动,速度为每秒1个单位,E点由B点向O点运动,速度为每秒2个单位,当一个点停上运动时,另一个点也随之停止,设运动时间为t(秒)
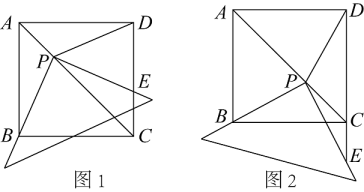
(1)、当t=s时,四边形EBFB'为正方形;(2)、当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?(3)、是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.7. 已知,如图:在直角坐标系中,正方形AOBC的边长为4,点D,E分别是线段AO,BO上的动点,D点由A点向O点运动,速度为每秒1个单位,E点由B点向O点运动,速度为每秒2个单位,当一个点停上运动时,另一个点也随之停止,设运动时间为t(秒)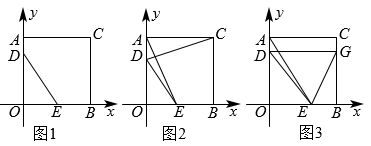 (1)、如图1,当t为何值时,△DOE的面积为6;(2)、如图2,连接CD,与AE交于一点,当t为何值时,CD⊥AE;(3)、如图3,过点D作DGOB,交BC于点G,连接EG,当D,E在运动过程中,使得点D,E,G三点构成等腰三角形,求出此时t的值.8. 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以4cm/秒的速度由B点向C点运动,同时,点Q在线段CD上以acm/秒的速度由C点向D点运动,设运动的时间为t秒,
(1)、如图1,当t为何值时,△DOE的面积为6;(2)、如图2,连接CD,与AE交于一点,当t为何值时,CD⊥AE;(3)、如图3,过点D作DGOB,交BC于点G,连接EG,当D,E在运动过程中,使得点D,E,G三点构成等腰三角形,求出此时t的值.8. 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以4cm/秒的速度由B点向C点运动,同时,点Q在线段CD上以acm/秒的速度由C点向D点运动,设运动的时间为t秒,①CP的长为 _▲_ cm(用含t的代数式表示);
②若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,求a的值.
 9. 如图,在Rt△ABC中,∠C=90°,∠A=45°,AC=10cm,点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动,同时点E从点B出发沿BA方向以 cm/s的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0<1≤10)s.过点E作EF⊥BC于点F,连接DE,DF。
9. 如图,在Rt△ABC中,∠C=90°,∠A=45°,AC=10cm,点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动,同时点E从点B出发沿BA方向以 cm/s的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0<1≤10)s.过点E作EF⊥BC于点F,连接DE,DF。 (1)、用含t的式子填空:BE= cm ,CD= cm。(2)、试说明,无论t为何值,四边形ADEF都是平行四边形;(3)、当t为何值时,△DEF为直角三角形?请说明理由。10. 已知,AB=18,动点P从点A出发,以每秒1个单位的速度向点B运动,分别以AP、BP为边在AB的同侧作正方形.设点P的运动时间为t.
(1)、用含t的式子填空:BE= cm ,CD= cm。(2)、试说明,无论t为何值,四边形ADEF都是平行四边形;(3)、当t为何值时,△DEF为直角三角形?请说明理由。10. 已知,AB=18,动点P从点A出发,以每秒1个单位的速度向点B运动,分别以AP、BP为边在AB的同侧作正方形.设点P的运动时间为t. (1)、如图1,若两个正方形的面积之和S,当t=6时,求出S的大小;(2)、如图2,当t取不同值时,判断直线AE和BC的位置关系,说明理由;(3)、如图3,用t表示出四边形EDBF的面积y.
(1)、如图1,若两个正方形的面积之和S,当t=6时,求出S的大小;(2)、如图2,当t取不同值时,判断直线AE和BC的位置关系,说明理由;(3)、如图3,用t表示出四边形EDBF的面积y.三、四边形中的线段最值问题
-
11. 如图,正方形ABCD的边长为4cm,动点E、F分别从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为cm.
 12. 在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,则运动时间t为秒时,P、C两点间的距离最小.
12. 在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,则运动时间t为秒时,P、C两点间的距离最小. 13. 如图,正方形的边长为3,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
13. 如图,正方形的边长为3,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )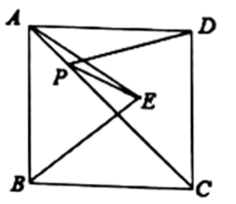 A、 B、 C、3 D、214. 如图,正方形ABCD的边长为4,点M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为( )
A、 B、 C、3 D、214. 如图,正方形ABCD的边长为4,点M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为( ) A、4 B、 C、 D、515. 如图,在边长为5的正方形中,点M为线段上一点,且 , 点P是对角线上一动点,过点P作于点E,于点F,则的最小值为( )
A、4 B、 C、 D、515. 如图,在边长为5的正方形中,点M为线段上一点,且 , 点P是对角线上一动点,过点P作于点E,于点F,则的最小值为( ) A、 B、 C、 D、16. 如图,已知正方形ABCD的边长为4,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是.
A、 B、 C、 D、16. 如图,已知正方形ABCD的边长为4,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是.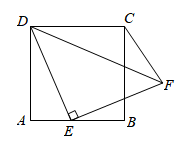
四、存在性问题
-
17. 如图,正方形ABCD的四个顶点分别在正方形EFGH的四条边上,我们称正方形EFGH是正方形ABCD的外接正方形.

探究一:已知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍?如图,假设存在正方形EFGH,它的面积是正方形ABCD的2倍.
因为正方形ABCD的面积为1,则正方形EFGH的面积为2,
所以EF=FG=GH=HE= , 设EB=x,则BF=﹣x,
∵Rt△AEB≌Rt△BFC
∴BF=AE=﹣x
在Rt△AEB中,由勾股定理,得
x2+(﹣x)2=12
解得,x1=x2=
∴BE=BF,即点B是EF的中点.
同理,点C,D,A分别是FG,GH,HE的中点.
所以,存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍
探究二:已知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的3倍?(仿照上述方法,完成探究过程)
探究三:已知边长为1的正方形ABCD, ▲ 一个外接正方形EFGH,它的面积是正方形ABCD面积的4倍?(填“存在”或“不存在”)
探究四:已知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的n倍?(n>2)(仿照上述方法,完成探究过程)
18. 在平面直角坐标系 中有 四点,其中 , .
(Ⅰ)在下图中描出 四点,再连接 ;
(II)直接写出线段 与线段 的位置关系;
(Ⅲ)若 与 轴交于点 与 轴交于点 ,在线段 上是否存在一点 ,使得三角形 与三角形 的面积相等.若存在,求点 的坐标;若不存在,请说明理由.
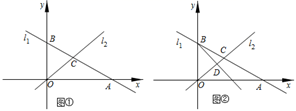
19. 在平面直角坐标系中,直线 : 分别与x轴、y轴交于点A、点B,且与直线 : 于点C.Ⅰ 如图 ,求出B、C两点的坐标;
Ⅱ 若D是线段OC上的点,且 的面积为4,求直线BD的函数解析式.
Ⅲ 如图 ,在 Ⅱ 的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
 20. 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
20. 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论 。
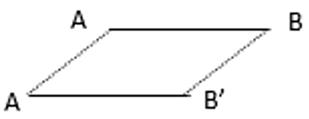
21. 如图所示,一条线段AB平移一段距离后得到线段A’B’,连接AA’,BB’可以得到一个平行四边形ABB’A’请据此回答下面问题:在平面直角坐标系中有A点(1,0),B点(-2,1),C点(-1,-3),若坐标平面内存在点D,使得A,B,C,D四点恰好能构成一个平行四边形,求D点的坐标.
五、综合训练
-
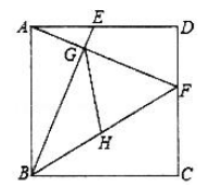
22. 如图,正方形 ABCD的边长为2,点E从点A出发沿着线段AD向点D运动(不与点A,D重合),同时点F从点D出发沿着线段DC向点C运动(不与点D,C重合,点E与点F的运动速度相同.BE与AF相交于点G,H为BF中点、则有下列结论:
①∠BGF是定值;②FB平分∠AFC:③当E运动到AD中点时,GH=:④当AG+BG= 时,四边形GEDF的面积是 ,其中正确的是( )
 A、①②④ B、①②③ C、①③④ D、②③④23. 如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
A、①②④ B、①②③ C、①③④ D、②③④23. 如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.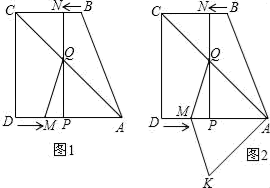 (1)、AM= , AP=.(用含t的代数式表示)(2)、当四边形ANCP为平行四边形时,求t的值(3)、如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
(1)、AM= , AP=.(用含t的代数式表示)(2)、当四边形ANCP为平行四边形时,求t的值(3)、如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,求AC.
24. 如图,正方形内有一点A ,以 , 为边向形外作正方形和正方形 , 连接 , .求证:.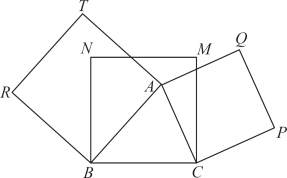 25. 如图,点在正方形的边上(不与 , 重合),连接 , 将线段绕点逆时针旋转得到 , 连接 . 求证:的面积 .
25. 如图,点在正方形的边上(不与 , 重合),连接 , 将线段绕点逆时针旋转得到 , 连接 . 求证:的面积 . 26. 如图1,已知正方形 , 是边上的一个动点不与点、重合 , 连结 , 点关于直线的对称点为 , 连结并延长交于点 , 连结 , .
26. 如图1,已知正方形 , 是边上的一个动点不与点、重合 , 连结 , 点关于直线的对称点为 , 连结并延长交于点 , 连结 , . (1)、求的度数.(2)、如图2,连结 , 若点为中点, , 求的面积.(3)、如图3,过点作于点 , 连结 , 请探究线段与的数量关系,并说明理由.27. 如图,正方形ABCD的顶点B在矩形AEFG的边EF上运动.
(1)、求的度数.(2)、如图2,连结 , 若点为中点, , 求的面积.(3)、如图3,过点作于点 , 连结 , 请探究线段与的数量关系,并说明理由.27. 如图,正方形ABCD的顶点B在矩形AEFG的边EF上运动.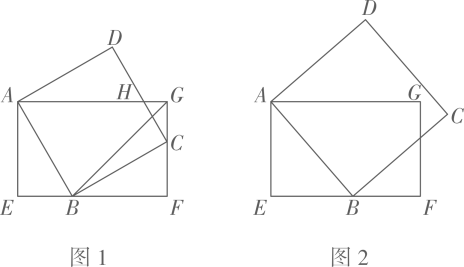 (1)、如图1,点C在FG上,求的大小;(2)、如图1,若C是FG的中点,求证:;(3)、如图2,若 , , 设 , , 直接写出y与x的函数解析式(不需要写自变量的取值范围).28.
(1)、如图1,点C在FG上,求的大小;(2)、如图1,若C是FG的中点,求证:;(3)、如图2,若 , , 设 , , 直接写出y与x的函数解析式(不需要写自变量的取值范围).28. (1)、【问题初探】如图1,E是正方形的边上一点,延长至点F,使 , 连接 , .求证:.(2)、【问题再探】如图2,E,M分别是正方形的边 , 上一点,分别过点M,E作于点P,于点Q,线段 , 相交于点N.连接 , , , , 若.
(1)、【问题初探】如图1,E是正方形的边上一点,延长至点F,使 , 连接 , .求证:.(2)、【问题再探】如图2,E,M分别是正方形的边 , 上一点,分别过点M,E作于点P,于点Q,线段 , 相交于点N.连接 , , , , 若.①求证:.
②探究和的面积关系,并说明理由.
(3)、【问题延伸】如图3,在正方形中,E,M分别是射线 , 上一点,【问题再探】中的其余条件不变,请直接判断和的面积关系是否仍成立.