人教版八年级下数学期末复习知识点扫盲满分计划——18.2.3正方形一
试卷更新日期:2023-06-11 类型:复习试卷
一、根据正方形性质求解角度数
-
1. 如图,E是正方形边延长线上的一点,且 .
 (1)、求的度数;(2)、若 , 求的面积.2. 如图,在正方形中,点E,F分别在边上, , , 则 .
(1)、求的度数;(2)、若 , 求的面积.2. 如图,在正方形中,点E,F分别在边上, , , 则 . 3. “勾股图”有着悠久的历史,欧几里得在《几何原本》中曾对它做了深入研究.如图,在△ABC中,∠ACB=90°,分别以△ABC的三条边为边向外作正方形.连接EB,CM,DG,CM分别与AB,BE相交于点P,Q.若∠AMP=30°,则∠ABE=°,的值为 .
3. “勾股图”有着悠久的历史,欧几里得在《几何原本》中曾对它做了深入研究.如图,在△ABC中,∠ACB=90°,分别以△ABC的三条边为边向外作正方形.连接EB,CM,DG,CM分别与AB,BE相交于点P,Q.若∠AMP=30°,则∠ABE=°,的值为 . 4. 如图,在正方形内作等边 , 连接 , , 则的度数为 .
4. 如图,在正方形内作等边 , 连接 , , 则的度数为 . 5. 如图,在正方形中,点在对角线上,且 , 延长交于点 , 连接 , 则的度数为 .
5. 如图,在正方形中,点在对角线上,且 , 延长交于点 , 连接 , 则的度数为 . 6. 如图,点M是正方形内位于对角线上方的一点, , 则的度数为 .
6. 如图,点M是正方形内位于对角线上方的一点, , 则的度数为 .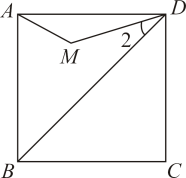
二、根据正方形性质求角长度
-
7. 如图 , 在正方形中,M是边上的一点,连接 , 作于点M,交正方形的外角的平分线于点N
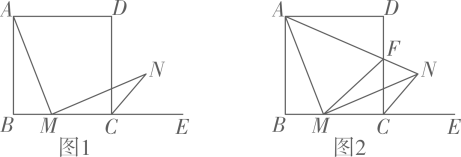 (1)、若正方形的边长为 , 当M是边上的中点时,求的长;(2)、求证:;(3)、如图2,连接 , 交边于点F,连接 , 探究线段、和之间的数量关系,并说明理由.8. 在正方形中,E为射线上一动点(点E不与A , B重合),作 , 交直线于点F , 连接 .
(1)、若正方形的边长为 , 当M是边上的中点时,求的长;(2)、求证:;(3)、如图2,连接 , 交边于点F,连接 , 探究线段、和之间的数量关系,并说明理由.8. 在正方形中,E为射线上一动点(点E不与A , B重合),作 , 交直线于点F , 连接 .
 (1)、如图1,当点E在线段上时,用等式表示线段 , , 的数量关系;(2)、如图2,当点E在线段的延长线上时,
(1)、如图1,当点E在线段上时,用等式表示线段 , , 的数量关系;(2)、如图2,当点E在线段的延长线上时,①依题意补全图2;
②用等式表示线段 , , 的数量关系,并证明.
9. 如图1,四边形ABCD为正方形,点M是对角线BD上的一点(0<BM<BD),连接AM,过点M作MN.⊥AM交CD于点N. (1)、求证:AM=MN.(2)、如图2,以MA,MN为邻边作矩形AMNP,连接PD.
(1)、求证:AM=MN.(2)、如图2,以MA,MN为邻边作矩形AMNP,连接PD.①求证:BM= PD;
②若正方形ABCD的边长为 , PD=4,求AM的长.
10. 如图1,把一个含角的直角三角板和一个正方形摆放在一起,使三角板的直角顶点和正方形的顶点重合,点、分别在正方形的边、上,连接 , 取中点 , 的中点 , 连接、. (1)、如图1,连接 , 求证:;(2)、在(1)的条件下,请判断线段与之间的数量关系,并加以证明;(3)、如图2,将这个含角的直角三角板的直角顶点和正方形的顶点重合,点、分别在正方形的边、的延长线上,其他条件不变,当 , 时,求的长.11. 如图,正方形边长为4,点E在边上(点E与点A、B不重合),过点A作 , 垂足为G,与边相交于点F.
(1)、如图1,连接 , 求证:;(2)、在(1)的条件下,请判断线段与之间的数量关系,并加以证明;(3)、如图2,将这个含角的直角三角板的直角顶点和正方形的顶点重合,点、分别在正方形的边、的延长线上,其他条件不变,当 , 时,求的长.11. 如图,正方形边长为4,点E在边上(点E与点A、B不重合),过点A作 , 垂足为G,与边相交于点F.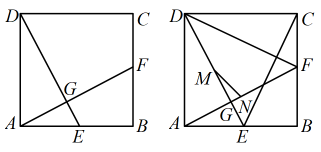 (1)、求证:;(2)、若的面积为 , 求的长;(3)、在(2)的条件下,取 , 的中点M,N,连接 , 求的长.
(1)、求证:;(2)、若的面积为 , 求的长;(3)、在(2)的条件下,取 , 的中点M,N,连接 , 求的长.三、根据正方形性质求面积
-
12. 如图,已知正方形的边长为 , 点E为对角线上一动点,连接 , 过 点E作 , 交射线于点F , 以 , 为邻边作矩形 , 连接 .
 (1)、 ;(2)、若 , 则矩形面积= .13. 如图,在四边形中, , 分别以四边形的四条边为边向外作四个正方形,面积依次为 , 下列结论正确的是( )
(1)、 ;(2)、若 , 则矩形面积= .13. 如图,在四边形中, , 分别以四边形的四条边为边向外作四个正方形,面积依次为 , 下列结论正确的是( )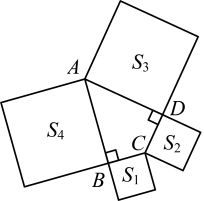 A、 B、 C、 D、14. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( )
A、 B、 C、 D、14. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( ) A、4 B、6 C、8 D、1215. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载,图(a)是由边长均为1的小正方形和Rt△BAC构成,可以用其面积关系验证勾股定理,将图(a)按图(b)所示的方式“嵌入”长方形LMJK,则该长方形的面积为( ).
A、4 B、6 C、8 D、1215. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载,图(a)是由边长均为1的小正方形和Rt△BAC构成,可以用其面积关系验证勾股定理,将图(a)按图(b)所示的方式“嵌入”长方形LMJK,则该长方形的面积为( ). A、60 B、100 C、110 D、12116. 如图,四边形中, , 且 , 以、、为边向外作正方形,其面积分别为 , , , 若 , 则的值为.
A、60 B、100 C、110 D、12116. 如图,四边形中, , 且 , 以、、为边向外作正方形,其面积分别为 , , , 若 , 则的值为. 17.(1)、【阅读理解】如图1, , 的面积与的面积相等吗?为什么?
17.(1)、【阅读理解】如图1, , 的面积与的面积相等吗?为什么?
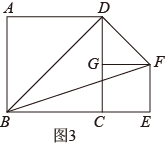
 (2)、【类比探究】问题①,如图2,在正方形的右侧作等腰 , , , 连接 , 求的面积.
(2)、【类比探究】问题①,如图2,在正方形的右侧作等腰 , , , 连接 , 求的面积.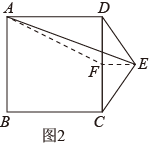 (3)、【拓展应用】问题②,如图3,在正方形的右侧作正方形 , 点B,C,E在同一直线上, , 连接 , , , 直接写出的面积.
(3)、【拓展应用】问题②,如图3,在正方形的右侧作正方形 , 点B,C,E在同一直线上, , 连接 , , , 直接写出的面积.
四、正方形的折叠问题
-
18. 如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE,折叠该纸片,使点A恰好落在AE上的G处,得到折痕BF,与AD交于点F.
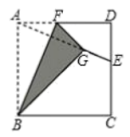 (1)、当E是CD的中点时,求AF的长;(2)、若 , 求GE的长.19. 如图,在正方形中,E是边的中点,将沿折叠,得到 , 延长交于G,连接 , .(1)、;(2)、;(3)、正方形的边长为 .
(1)、当E是CD的中点时,求AF的长;(2)、若 , 求GE的长.19. 如图,在正方形中,E是边的中点,将沿折叠,得到 , 延长交于G,连接 , .(1)、;(2)、;(3)、正方形的边长为 . 20. 如图,在正方形 中, ,点 在边 上,且 ,将 沿 折叠得到 ,延长 交边 于点 ,则 的长为( )
20. 如图,在正方形 中, ,点 在边 上,且 ,将 沿 折叠得到 ,延长 交边 于点 ,则 的长为( ) A、2 B、 C、3 D、21. 综合与实践
A、2 B、 C、3 D、21. 综合与实践折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图①:点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN , MN , AN , 如图②
 (1)、图②中,.线段F=.(2)、图②中,试判断的形状,并给出证明.
(1)、图②中,.线段F=.(2)、图②中,试判断的形状,并给出证明.剪一剪、折一折:将图②中的剪下来,将其沿直线GH折叠,使点A落在点处,分别得到图③、图④.
(3)、图③中,若 , 则°22. 如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD= .
五、正方形的判定
-
23. 如图,在中, , D、E、F分别是、、的中点.
 (1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.24. 如图,在中, , 过点C的直线 , D为边上一点,过点D作 , 交直线于E,垂足为F,连接、 .
(1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.24. 如图,在中, , 过点C的直线 , D为边上一点,过点D作 , 交直线于E,垂足为F,连接、 .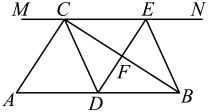 (1)、求证:;(2)、当D在中点时,四边形是什么特殊四边形?请说明你的理由;(3)、若D为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.25. 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)、求证:;(2)、当D在中点时,四边形是什么特殊四边形?请说明你的理由;(3)、若D为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.25. 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.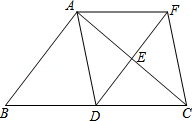 (1)、求证:四边形ADCF是平行四边形;(2)、当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.26. 如图所示,在正方形ABCD中,对角线BD所在的直线上有两点E,F满足BE=DF,连接AE,AF,CE,CF.
(1)、求证:四边形ADCF是平行四边形;(2)、当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.26. 如图所示,在正方形ABCD中,对角线BD所在的直线上有两点E,F满足BE=DF,连接AE,AF,CE,CF. (1)、求证:△CBE≌△CDF;(2)、试判断四边形AECF的形状,并说明理由.27. 如图,是的角平分线, , , 垂足分别是E、F,连接 , 与相交千点H.
(1)、求证:△CBE≌△CDF;(2)、试判断四边形AECF的形状,并说明理由.27. 如图,是的角平分线, , , 垂足分别是E、F,连接 , 与相交千点H. (1)、求证:;(2)、满足什么条件时,四边形是正方形?说明理由.
(1)、求证:;(2)、满足什么条件时,四边形是正方形?说明理由.六、中点四边形
-
28. 我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.(1)、如图1,在四边形中,点 , , , 分别为边 , , , 的中点.求证中点四边形是平行四边形;
 (2)、如图2,点是四边形内一点,且满足 , , , 点 , , , 分别为边 , , , 的中点,猜想中点四边形的形状,并证明你的猜想;
(2)、如图2,点是四边形内一点,且满足 , , , 点 , , , 分别为边 , , , 的中点,猜想中点四边形的形状,并证明你的猜想; (3)、若改变(2)中的条件,使 , 其他条件不变,请判断中点四边形的形状,并说明理由.29. 我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.如图,E、F、G、H分别是四边形各边的中点.
(3)、若改变(2)中的条件,使 , 其他条件不变,请判断中点四边形的形状,并说明理由.29. 我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.如图,E、F、G、H分别是四边形各边的中点. (1)、求证:四边形是平行四边形;(2)、如果我们对四边形的对角线与添加一定的条件,则可使四边形成为特殊的平行四边形,请你经过探究后直接填写答案:
(1)、求证:四边形是平行四边形;(2)、如果我们对四边形的对角线与添加一定的条件,则可使四边形成为特殊的平行四边形,请你经过探究后直接填写答案:①当时,四边形为;
②当时,四边形为矩形;
③当且时,四边形为 .
30. 顺次连接四边形各边中点所得的四边形叫中点四边形.回答下列问题:(1)、只要原四边形的两条对角线 , 就能使中点四边形是菱形;(2)、只要原四边形的两条对角线 , 就能使中点四边形是矩形;(3)、请你设计一个中点四边形为正方形,但原四边形又不是正方形的四边形,把它画出来.31. 综合与实践问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E , F , G , H分别为边AB , BC , CD , DA的中点.试说明中点四边形EFGH是平行四边形.

探究展示:勤奋小组的解题思路:
反思交流:
(1)、①上述解题思路中的“依据1”、“依据2”分别是什么?依据1:;依据2:;
②连接AC , 若AC=BD时,则中点四边形EFGH的形状为;
(2)、如图(2),点P是四边形ABCD内一点,且满足PA=PB , PC=PD , ∠APB=∠CPD , 点E , F , G , H分别为边AB , BC , CD , DA的中点,猜想中点四边形EFGH的形状,并说明理由;(3)、若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .七、利用(特殊)平行四边形的对称性求阴影面积
-
32. 如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( )
 A、2 B、4 C、8 D、33. 如图,中∠ACB是直角,分别以的三边向外作正方形,G为边EF的中点,若要求出图中阴影的面积,只需要知道线段( )
A、2 B、4 C、8 D、33. 如图,中∠ACB是直角,分别以的三边向外作正方形,G为边EF的中点,若要求出图中阴影的面积,只需要知道线段( ) A、AB的长度 B、AC的长度 C、BC的长度 D、BG的长度
A、AB的长度 B、AC的长度 C、BC的长度 D、BG的长度


