人教版八年级下数学期末复习知识点扫盲满分计划——18.2.1矩形的判定
试卷更新日期:2023-06-11 类型:复习试卷
一、矩形的判定
-
1. 如图,平行四边形中,点E,F分别在边 , 上, , . 连接 , .
 (1)、求证:四边形是矩形;(2)、若 , , 平分 , 求的长.2. 如图, , 平分 , 平分 . , . 求证:四边形是矩形.
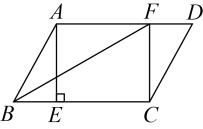
(1)、求证:四边形是矩形;(2)、若 , , 平分 , 求的长.2. 如图, , 平分 , 平分 . , . 求证:四边形是矩形. 3. 如图,在平行四边形中,过点作于点点在边上,连接AF,BF.
3. 如图,在平行四边形中,过点作于点点在边上,连接AF,BF.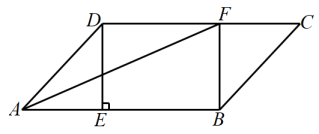 (1)、求证:四边形是矩形;(2)、若平分求四边形的面积.4. 如图,中,点O是边上的一个动点,过点O作直线 , 交的平分线于点E , 交的外角平分线于点F .
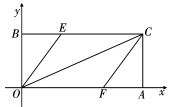
(1)、求证:四边形是矩形;(2)、若平分求四边形的面积.4. 如图,中,点O是边上的一个动点,过点O作直线 , 交的平分线于点E , 交的外角平分线于点F . (1)、判断与的大小关系?并说明理由;(2)、当点O运动到何处时,四边形是矩形?并说出你的理由;5. 如图1,在中, , 于点C,点E是的中点,连接并延长,使 , 连接.
(1)、判断与的大小关系?并说明理由;(2)、当点O运动到何处时,四边形是矩形?并说出你的理由;5. 如图1,在中, , 于点C,点E是的中点,连接并延长,使 , 连接.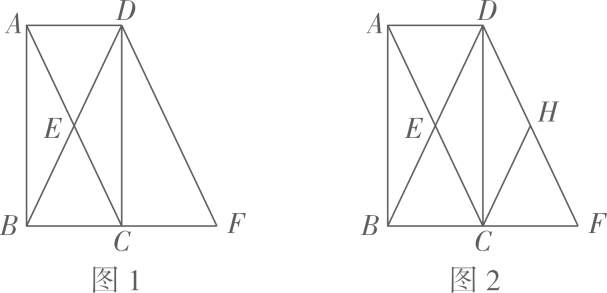 (1)、求证:四边形是矩形.(2)、如图2,点H为的中点,连结 , 若 , , 求四边形的面积.
(1)、求证:四边形是矩形.(2)、如图2,点H为的中点,连结 , 若 , , 求四边形的面积.二、添一条件使四边形是矩形
-
6. 如图,在△ABC中,点D是BC的中点,点E是AD边的中点,过点A作AF∥CB交CE的延长线于点F,连接BF.
 (1)、求证:AF=BD;(2)、当△ABC满足什么条件时,四边形BDAF为矩形,并说明理由.7. 如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
(1)、求证:AF=BD;(2)、当△ABC满足什么条件时,四边形BDAF为矩形,并说明理由.7. 如图,要使平行四边形ABCD成为矩形,需添加的条件是( ) A、AB=BC B、AC⊥BD C、∠1=∠2 D、∠ABC=90°8. 要使平行四边形 成为矩形,需要添加的条件是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,点E,点F分别是AC,BC的中点,D是斜边AB上一点,则添加下列条件可以使四边形DECF成为矩形的是( )
A、AB=BC B、AC⊥BD C、∠1=∠2 D、∠ABC=90°8. 要使平行四边形 成为矩形,需要添加的条件是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,点E,点F分别是AC,BC的中点,D是斜边AB上一点,则添加下列条件可以使四边形DECF成为矩形的是( ) A、∠ACD=∠BCD B、AD=BD C、CD⊥AB D、CD=AC10. 如图,在中,AE⊥BC于点E,点F在BC边的延长线上,只需再添加一个条件即可证明四边形AEFD是矩形,这个条件可以是(写出一个即可).
A、∠ACD=∠BCD B、AD=BD C、CD⊥AB D、CD=AC10. 如图,在中,AE⊥BC于点E,点F在BC边的延长线上,只需再添加一个条件即可证明四边形AEFD是矩形,这个条件可以是(写出一个即可).
三、线段最小值问题
-
11. 如图,在中, , , , P为边上任意一点(点P与点C不重合),连接 , 以 , 为邻边作 , 连接 , 则长的最小值是 .
 12. 如图,在矩形中, , 点M,N,P分别在 , , 上运动,且四边形的面积始终等于24,则的最小值是 ( )
12. 如图,在矩形中, , 点M,N,P分别在 , , 上运动,且四边形的面积始终等于24,则的最小值是 ( ) A、10 B、12 C、14 D、1613. 如图,在矩形中,为线段上一动点,于点于点Q,则的最小值为( )
A、10 B、12 C、14 D、1613. 如图,在矩形中,为线段上一动点,于点于点Q,则的最小值为( ) A、 B、 C、 D、14. 如图,在矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值为( )
A、 B、 C、 D、14. 如图,在矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值为( ) A、 B、3 C、 D、15. 如图,在矩形中, , , 为边的中点,点在线段上运动,是的中点,则的周长的最小值是.
A、 B、3 C、 D、15. 如图,在矩形中, , , 为边的中点,点在线段上运动,是的中点,则的周长的最小值是.
四、矩形性质和判定综合
-
16. 如图,在矩形中,O为中点,过O点且分别交于F , 交于E , 点G是中点且 , 则下列结论正确的个数为( )
 (1)、 ;(2);(3)是等边三角形;(4)A、1个 B、2个 C、3个 D、4个17. 已知中, , F是的中点,作 , 垂足E在线段上,不与点C重合,连接 , 下列结论:①;②;③;④中一定成立的是( )
(1)、 ;(2);(3)是等边三角形;(4)A、1个 B、2个 C、3个 D、4个17. 已知中, , F是的中点,作 , 垂足E在线段上,不与点C重合,连接 , 下列结论:①;②;③;④中一定成立的是( ) A、①②④ B、①③④ C、①②③ D、①②③④18. 如图,BE,BF分别是与它的邻补角的平分线, , 垂足为点E, , 垂足为点F,EF分别交边AB,AC于点M和N.若 , , 则的长为 .
A、①②④ B、①③④ C、①②③ D、①②③④18. 如图,BE,BF分别是与它的邻补角的平分线, , 垂足为点E, , 垂足为点F,EF分别交边AB,AC于点M和N.若 , , 则的长为 .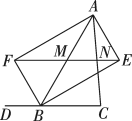 19. 如图,在矩形中, , E是的中点,于点F,则的长是( )
19. 如图,在矩形中, , E是的中点,于点F,则的长是( ) A、1 B、1.2 C、 D、220. 如图,四边形和四边形是两个矩形,点在边上,若 , , 则矩形的面积为
A、1 B、1.2 C、 D、220. 如图,四边形和四边形是两个矩形,点在边上,若 , , 则矩形的面积为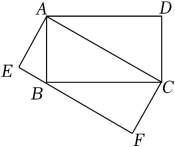 A、2 B、 C、 D、
A、2 B、 C、 D、五、综合训练
-
21. 如图所示,在直角梯形ABCD中,AD∥BC , ∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
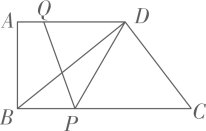 (1)、设△DPQ的面积为S , 求S与t之间的关系式;(2)、当t为何值时,四边形PCDQ是平行四边形?(3)、分别求出当t为何值时,①PD=PQ;②DQ=PQ .22. 如图,在▱ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)、设△DPQ的面积为S , 求S与t之间的关系式;(2)、当t为何值时,四边形PCDQ是平行四边形?(3)、分别求出当t为何值时,①PD=PQ;②DQ=PQ .22. 如图,在▱ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.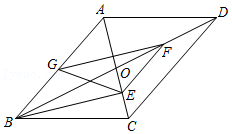 (1)、求证:∠OBE=∠ADO;(2)、若F、G分别是OD、AB的中点,且BC= ,
(1)、求证:∠OBE=∠ADO;(2)、若F、G分别是OD、AB的中点,且BC= ,①求证:△EFG是等腰三角形;
②当EF⊥EG时,求▱ABCD的面积.
23. (1)、如图1,在中,= , 是的中点,是的中点,若 , , 求的长.(2)、如图2,在平行四边形中,是的中点,是上的中点,若 , , , 求的长.24. 如图,在矩形中, , , M为线段上一动点,于点P,于点Q,则的最小值为 .
(1)、如图1,在中,= , 是的中点,是的中点,若 , , 求的长.(2)、如图2,在平行四边形中,是的中点,是上的中点,若 , , , 求的长.24. 如图,在矩形中, , , M为线段上一动点,于点P,于点Q,则的最小值为 . 25. 如图,矩形ABCD中,AB=4,AD=3,点E是边BC的中点,连接AE,把△ABE沿AE对折得到△AFE,延长AF与CD交于点G,则DG的长为 .
25. 如图,矩形ABCD中,AB=4,AD=3,点E是边BC的中点,连接AE,把△ABE沿AE对折得到△AFE,延长AF与CD交于点G,则DG的长为 . 26. 如图,在四边形ABCD中,AB//CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为 .
26. 如图,在四边形ABCD中,AB//CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为 . 27. 如图,△ABC中,D,E分别为AB,BC的中点,DG⊥AC,EF⊥AC,垂足分别为G,F.
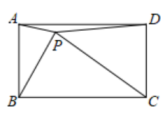
27. 如图,△ABC中,D,E分别为AB,BC的中点,DG⊥AC,EF⊥AC,垂足分别为G,F.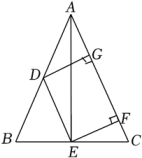 (1)、求证:四边形DEFG为矩形;(2)、若AB=AC=2 , EF=2,求CF的长.28. 已知矩形ABCD中有一点P,满足PA=1,PB=2,PC=3,则PD= .
(1)、求证:四边形DEFG为矩形;(2)、若AB=AC=2 , EF=2,求CF的长.28. 已知矩形ABCD中有一点P,满足PA=1,PB=2,PC=3,则PD= .