人教版八年级下数学期末复习知识点扫盲满分计划——18.2.1矩形的性质
试卷更新日期:2023-06-11 类型:复习试卷
一、利用矩形性质求角度
-
1. 如图,在矩形中,对角线 , 相交于点 , 过点作于点 , 过点作于点.
 (1)、求证:≌;(2)、若 , 求的度数.2. 点P是矩形的对角线的延长线上一点, , , 则度.
(1)、求证:≌;(2)、若 , 求的度数.2. 点P是矩形的对角线的延长线上一点, , , 则度. 3. 如图,中, , 是对角线上两点, , , , 则 .
3. 如图,中, , 是对角线上两点, , , , 则 .
 4. 如图,在长方形中, , , E为边上的中点,点F从点B出发,以每秒1个单位长度的速度沿着边向终点C运动,连接 , , . 设点F运动的时间为t秒.
4. 如图,在长方形中, , , E为边上的中点,点F从点B出发,以每秒1个单位长度的速度沿着边向终点C运动,连接 , , . 设点F运动的时间为t秒. (1)、当t为何值时,?(2)、是否存在某一时刻,使得?如果存在,求出t的值;如果不存在,说明理由.5. 如图,在矩形中,对角线相交于点O, , 交于F,垂足为E,求的度数.
(1)、当t为何值时,?(2)、是否存在某一时刻,使得?如果存在,求出t的值;如果不存在,说明理由.5. 如图,在矩形中,对角线相交于点O, , 交于F,垂足为E,求的度数.
二、根据矩形性质求线段长度
-
6. 如图,矩形的对角线相交于点O, , , 则边的长为( )
 A、3 B、4 C、 D、7. 如图,矩形的对角线相交于点O , , , 则矩形对角线的长为( )
A、3 B、4 C、 D、7. 如图,矩形的对角线相交于点O , , , 则矩形对角线的长为( )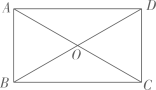 A、4 B、8 C、 D、8. 如图,在矩形中,O是对角线中点.过O点的直线与矩形的一组对边 , 分别相交于点F , E .
A、4 B、8 C、 D、8. 如图,在矩形中,O是对角线中点.过O点的直线与矩形的一组对边 , 分别相交于点F , E . (1)、求证:;(2)、点与B关于直线对称,连接 .
(1)、求证:;(2)、点与B关于直线对称,连接 .①求证:;
②若 , 且四边形是平行四边形,求线段长.
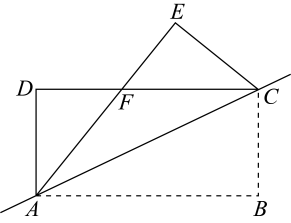
9. 如图,是矩形的边上一个动点,矩形的两条边、的长分别为3和4,那么点到矩形的两条对角线和的距离之和是( ) A、 B、 C、 D、10. 如图,在矩形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,若AB=6,BC=10,则GH的长度为( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,若AB=6,BC=10,则GH的长度为( ) A、 B、 C、 D、2
A、 B、 C、 D、2三、根据矩形性质求面积
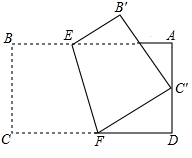
-
11. 如图,矩形纸片中, , 把矩形纸片沿直线折叠,点B落在点E处,交于点F , 若 . 求的面积.
 12. 如图,在矩形中,对角线相交于点O,于点E,于点F,连接 .
12. 如图,在矩形中,对角线相交于点O,于点E,于点F,连接 . (1)、求证:四边形是平行四边形;(2)、若 , 求四边形的面积.13. 如图,在中, , 分别以 , , 为边在的同一侧作正方形 , , , 四块阴影部分的面积分别为 , , , .若已知图中阴影部分的面积的和,则一定能求出( )
(1)、求证:四边形是平行四边形;(2)、若 , 求四边形的面积.13. 如图,在中, , 分别以 , , 为边在的同一侧作正方形 , , , 四块阴影部分的面积分别为 , , , .若已知图中阴影部分的面积的和,则一定能求出( )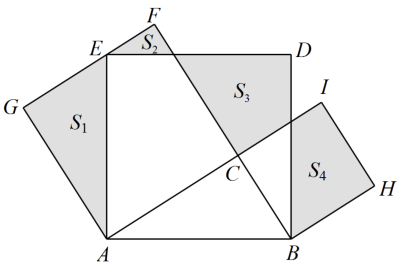 A、正方形的面积 B、正方形的面积 C、的面积 D、四边形的面积14. 如图,长方形ABCD是由30个大小相等的正方形拼成的,E、F、G、H分别在AD、 AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则长方形ABCD的面积是( )
A、正方形的面积 B、正方形的面积 C、的面积 D、四边形的面积14. 如图,长方形ABCD是由30个大小相等的正方形拼成的,E、F、G、H分别在AD、 AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则长方形ABCD的面积是( )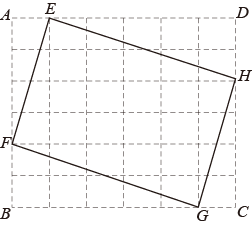 A、2 B、 C、 D、15. 如图,在矩形ABCD中,BC=4,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是( )
A、2 B、 C、 D、15. 如图,在矩形ABCD中,BC=4,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是( ) A、2 B、4 C、8 D、
A、2 B、4 C、8 D、四、求矩形在坐标系中的坐标
-
16. 如图,矩形的顶点B的坐标为 , 则长为( )
 A、 B、 C、 D、417. 已知在平面直角坐标系中,矩形的三个顶点的坐标为 , , , 则第四个顶点的坐标为( )A、 B、 C、( D、18. 已知矩形中, , , , 则矩形的面积为.
A、 B、 C、 D、417. 已知在平面直角坐标系中,矩形的三个顶点的坐标为 , , , 则第四个顶点的坐标为( )A、 B、 C、( D、18. 已知矩形中, , , , 则矩形的面积为. 19. 已知 , , , , 动点P从点A出发,在线段上,以每秒1个单位的速度向点D运动:动点Q从点C出发,在线段上,以每秒2个单位的速度向点B运动,点P、Q同时出发,当其中一个点到达终点时,另一个点随之停止运动,设运动时间为t(秒).
19. 已知 , , , , 动点P从点A出发,在线段上,以每秒1个单位的速度向点D运动:动点Q从点C出发,在线段上,以每秒2个单位的速度向点B运动,点P、Q同时出发,当其中一个点到达终点时,另一个点随之停止运动,设运动时间为t(秒).
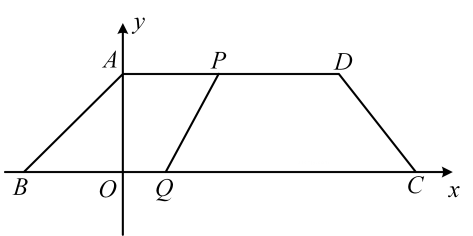 (1)、当秒时,平分线段;(2)、当秒时,轴;(3)、当时,求t的值.20. 如图:在平面直角坐标系内有长方形 , 点A,C分别在y轴,x轴上,点在上,点E在上,沿折叠,使点B与点O重合,点C与点重合.若点P在坐标轴上,且面积是18,则点P坐标为 .
(1)、当秒时,平分线段;(2)、当秒时,轴;(3)、当时,求t的值.20. 如图:在平面直角坐标系内有长方形 , 点A,C分别在y轴,x轴上,点在上,点E在上,沿折叠,使点B与点O重合,点C与点重合.若点P在坐标轴上,且面积是18,则点P坐标为 .
五、矩形与折叠问题
-
21. 如图,长方形纸片ABCD中,AD=4,AB=10,按如图的方式折叠,使点B与点D重合,折痕为EF,则DE长为( )
 A、4.8 B、5 C、5.8 D、622. 如图,已知点是长方形中边上一点,将四边形沿直线折叠,折叠后点的对应点为 , 点的对应点为 , 若点在上,且 , , 则 .
A、4.8 B、5 C、5.8 D、622. 如图,已知点是长方形中边上一点,将四边形沿直线折叠,折叠后点的对应点为 , 点的对应点为 , 若点在上,且 , , 则 .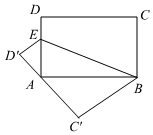 23. 如图:长方形的边沿折叠, 使点D落在上的点F处, 已知 , 的面积是24, 则的值为
23. 如图:长方形的边沿折叠, 使点D落在上的点F处, 已知 , 的面积是24, 则的值为 24. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=36°,则∠GHC等于( )
24. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=36°,则∠GHC等于( ) A、110° B、108° C、106° D、112°25. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , 若 , 则 度
A、110° B、108° C、106° D、112°25. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , 若 , 则 度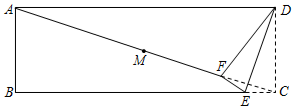
六、斜边上的中线等于斜边一半
-
26. 如图,在中, , 点D是AB的中点,且 , 则AB=cm.
 27. 如图,为的中位线,点在上,且 , 若 , , 则的长为 .
27. 如图,为的中位线,点在上,且 , 若 , , 则的长为 . 28. 如图,在中,对角线 , 相交于点O. , E,F,G分别是 , , 的中点.
28. 如图,在中,对角线 , 相交于点O. , E,F,G分别是 , , 的中点. (1)、求证:;(2)、若 , 求的长.29. 如图
(1)、求证:;(2)、若 , 求的长.29. 如图 (1)、【问题提出】
(1)、【问题提出】
如图1,在中, , , 是等边三角形,点在边上,探究与的数量关系.(2)、【问题探究】
先将问题特殊化如图1,当点在边上时,猜想和数量关系,并加以证明;(3)、再探究一般情形如图2,当点在内部时,证明(1)中的结论仍然成立.(4)、【问题拓展】
如图3,当点在外部时,于点 , 过点作 , 交线段的延长线于点 , , 直接写出的长 .30. (1)、如图1,在中,= , 是的中点,是的中点,若 , , 求的长.(2)、如图2,在平行四边形中,是的中点,是上的中点,若 , , , 求的长.
(1)、如图1,在中,= , 是的中点,是的中点,若 , , 求的长.(2)、如图2,在平行四边形中,是的中点,是上的中点,若 , , , 求的长.七、综合训练
-
31. 如图,矩形ABCD中,AB=2 ,BC=4,连结对角线AC,E为AC的中点,F为AB边上的动点,连结EF,作点C关于EF的对称点C′,连结C′E,C′F,若△EFC′与△ACF的重叠部分(△EFG)面积等于△ACF的 ,则BF=.
 32. 如图,矩形 , 点E为上一点,连接 , 在上取一点F,连接 , 过F作的垂线交于点H,若 , , , , 则的长是 .
32. 如图,矩形 , 点E为上一点,连接 , 在上取一点F,连接 , 过F作的垂线交于点H,若 , , , , 则的长是 . 33. 在平行四边形中, , 为中点,点在线段上,连接 , 在下方有一点 , 满足 , 连接 .
33. 在平行四边形中, , 为中点,点在线段上,连接 , 在下方有一点 , 满足 , 连接 . (1)、若 , , 求的面积;(2)、若 , , 求证: .34. 如图,在中, , , , 是上一动点,过点作于点 , 于点 . 连接 , 则线段的最小值是 .
(1)、若 , , 求的面积;(2)、若 , , 求证: .34. 如图,在中, , , , 是上一动点,过点作于点 , 于点 . 连接 , 则线段的最小值是 . 35. 问题探究:
35. 问题探究: (1)、如图1,中, , , 是高,求证:.(2)、如图2,在(1)条件下,、分别是和上的点,且 , 如果 , 那么四边形的面积是;(3)、如图3,四边形中,平分 , , , , 求的值.36. 如图1,在中,分别是边上的高线,M,N分别是线段的中点.
(1)、如图1,中, , , 是高,求证:.(2)、如图2,在(1)条件下,、分别是和上的点,且 , 如果 , 那么四边形的面积是;(3)、如图3,四边形中,平分 , , , , 求的值.36. 如图1,在中,分别是边上的高线,M,N分别是线段的中点. (1)、求证:.(2)、连接 , 猜想与之间的关系,并说明理由.(3)、若将锐角三角形变为钝角三角形 , 其余条件不变,如图2,直接写出与之间的关系.37. 如图1是长方形纸带将长方形ABCD沿EF折叠成图2,使点C、D分别落在点 、 处,再沿BF折叠成图3,使点 、 分别落在点 、 处.
(1)、求证:.(2)、连接 , 猜想与之间的关系,并说明理由.(3)、若将锐角三角形变为钝角三角形 , 其余条件不变,如图2,直接写出与之间的关系.37. 如图1是长方形纸带将长方形ABCD沿EF折叠成图2,使点C、D分别落在点 、 处,再沿BF折叠成图3,使点 、 分别落在点 、 处. (1)、若 ,求图1中 的度数;(2)、在(1)的条件下,求图2中 的度数;(3)、在图3中写出 、 与 的数量关系,并说明理由.38. 如图,矩形ABCD中,CD=8,AD=4,将矩形沿AC折叠,点D落在点D′处,求重叠部分△AFC 的面积.
(1)、若 ,求图1中 的度数;(2)、在(1)的条件下,求图2中 的度数;(3)、在图3中写出 、 与 的数量关系,并说明理由.38. 如图,矩形ABCD中,CD=8,AD=4,将矩形沿AC折叠,点D落在点D′处,求重叠部分△AFC 的面积.