吉林省2022-2023学年八年级下学期数学期末考试模拟卷（四）

试卷更新日期：2023-06-10 类型：复习试卷

进入出卷网下载

一、单选题

1. 若 $y = k x - 4$ 的函数值y随x的增大而增大，则k的值可能是下列的（）

A、-4 B、 $- \frac{1}{2}$ C、0 D、3

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{3} + \sqrt{4} = \sqrt{7}$ B、 ${(- \sqrt{3})}^{2} = - 3$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$

查看试题解析
3. 直线y＝x+2与y＝﹣x+4的交点在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 某同学这学期前四次数学测验的成绩依次为93、82、76和88，马上要进行第五次数学测验了，她这五次成绩的平均数能够达到或超过85分，那么，这次测验她的分数至少是（）

A、83 B、84 C、85 D、86

查看试题解析
5. 函数 $y = (m + 1) x^{m^{2}}$ 是正比例函数，则m的值为（）

A、 $± 1$ B、1 C、 $- 1$ D、不存在

查看试题解析
6. 如图，一个长方体铁块放置在圆柱形水槽容器内，向容器内按一定的速度均匀注水，60秒后将容器内注满.容器内水面的高度h（cm）与注水时间t（s）之间的函数关系图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 计算： $\sqrt{24} \times \sqrt{\frac{1}{6}} =$ ．

查看试题解析
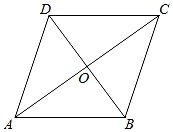
8. 函数y= $\sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
9. 如图，四边形ABCD是边长为 $\sqrt{5}$ cm的菱形，其中对角线BD的长为2cm，则菱形ABCD的面积为 cm² ．

查看试题解析
10. 在平面直角坐标系中，若点 $(- 2 ， y_{1})$ 、 $(1 ， y_{2})$ 、 $(- 1 ， y_{3})$ 都在函数 $y = \frac{k}{x} (k < 0)$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（用“＞”号连接）．

查看试题解析
11. 若 $| a + 2 | + \sqrt{b - 3} = 0$ ，则直线 $y = a x + b$ 不经过第象限．

查看试题解析
12. 如图，在正方形ABCD的外侧，作等边△ADE，则∠ABE的度数为．

查看试题解析
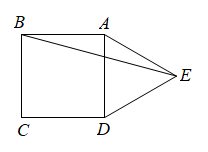13. 函数 $y = k x + b$ 的图像如图所示，则关于x的不等式 $k x + b < 0$ 的解集是．

查看试题解析
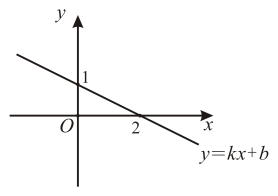14. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是．

查看试题解析

三、解答题

15. 计算：3 $\sqrt{3}$ ﹣ $\sqrt{8}$ + $\sqrt{2}$ ﹣ $\sqrt{27}$ ．

查看试题解析
16. 先化简，再求值：当 $a = 9$ 时，求 $a + \sqrt{1 - 2 a + a^{2}}$ 的值．小宁的解答过程如下：
原式＝ $a + \sqrt{(1 - a)^{2}}$ 第一步
$= a + 1 - a$ 第二步
＝1 第三步

(1)、小宁的解答从第步出现错误的，错误的原因是．

(2)、写出正确的解答过程：

查看试题解析
17. 如图，有一架秋千，当它静止时，踏板离地的垂直高度DE＝1m，将它往前推送4m（水平距离BC＝4m）时，秋千的踏板离地的垂直高度BF＝2m，秋千的绳索始终拉得很直，求绳索AD的长度．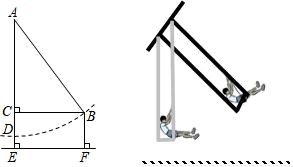

查看试题解析
18. 如图，在平行四边形ABCD中，点E，F分别在AD，BC上，且AE＝CF，连接BE，DF．求证：BE＝DF．

查看试题解析
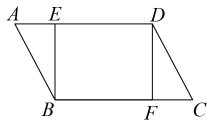19. 若 $y = (m + 1) x^{| m + 2 |} - 2 n + 8$ 是正比例函数，求m，n的值．

查看试题解析
20. 在抗击新冠病毒疫情的“战斗”中，我们团结一心，众志成城，取得了最终的胜利．企业复工复产后，某企业生产部统计了15名工人某天的加工零件数，如下表：
每人加工零件数
18
16
10
8
7
6
人数
1
1
2
6
3
2

(1)、求出这15名工人该天加工零件数的平均数．

(2)、写出这15名工人该天加工零件数的中位数和众数；

(3)、若你是这个企业生产部领导，为了调动多数工人的积极性，会将每位工人的日加工零件任务数定为9件吗？为什么？

查看试题解析
21. 小明和小红分别从甲、乙两地沿同一条路同时出发，相向而行．小明从甲地到乙地，小红从乙地到甲地，小明和小红离甲地的距离y（千米）与时间x（小时）之间的函数图象如图所示，根据图中提供的信息，解答下列问题：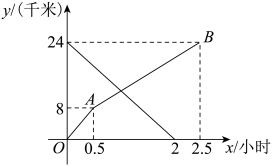

(1)、小红出发后速度为千米/小时．

(2)、求线段AB对应的函数表达式，写出自变量x的取值范围．

(3)、当小红到达甲地时，小明距乙地还有多远？

查看试题解析
22. 【阅读材料】如图①，在边长为4的正方形ABCD中，点E、F分别在边BC、CD上且∠EAF＝45°，连接EF，求△CEF的周长．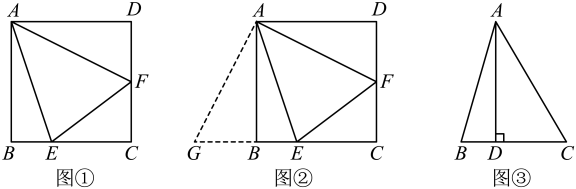
小明想到解决问题的方法如下：
如图②，延长CB至点G，使BG＝DF，通过证明 $△ A G E ≌ △ A F E$ ，得到BE、DF、EF之间的关系，进而求出△CEF的周长．

(1)、请按照小明的思路，帮助小明写出完整的求解过程．

(2)、【方法应用】如图②，若BE＝1，求DF的长．

(3)、【能力提升】如图③，在锐角△ABC中，∠BAC＝45°，AD⊥BC于点D．若BD＝1，AD＝4，则CD的长为．

查看试题解析
23. 如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4 $\sqrt{2}$ 米．

(1)、求新传送带AC的长度．

(2)、如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点5米的货物MNQP是否需要挪走，并说明理由．
参考数据： $\sqrt{2} \approx 1.4 ， \sqrt{3} \approx 1.7$ ．

查看试题解析
24. 如图，等腰△ABC中，已知AC＝BC＝ $\sqrt{10}$ ，AB＝2，作∠ACB的外角平分线CF，点E从点B沿着射线BA以每秒1个单位的速度运动，过点E作BC的平行线交CF于点F.

(1)、求证：四边形BCFE是平行四边形；

(2)、当点E是边AB的中点时，连接AF，试判断四边形AECF的形状，并说明理由；

(3)、设运动时间为t秒，是否存在t的值，使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形？不存在的，试说明理由；存在的，请直接写出t的值.

查看试题解析

每人加工零件数	18	16	10	8	7	6
人数	1	1	2	6	3	2