吉林省2022-2023学年八年级下学期数学期末考试模拟卷（二）
试卷更新日期：2023-06-10 类型：复习试卷
一、单选题
-
1. 一个纳米粒子的直径是35纳米（1纳米米），用科学记数法表示为（ ）A、米 B、米 C、米 D、米2. 某气象台为了预报台风，首先需要确定台风中心的位置，则下列说法能确定台风中心位置的是（ ）A、北纬38° B、距气象台500海里 C、海南附近 D、北纬38°，东经136°3. 若分式的值为0，则x的值是（ ）A、3或﹣3 B、﹣3 C、0 D、34. 某校将举办一场“中国汉字听写大赛”，要求各班推选一名同学参加比赛，为此，八年二班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学的平均分都是97分，甲的成绩的方差是0.3，乙的成绩的方差是0.7．根据以上数据，下列说法正确的是（ ）A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定5. 如图，AB∥DC，ED∥BC，AE∥BD，那么图中和△ABD面积相等的三角形（不包括△ABD）有（ ）
A、1个 B、2个 C、3个 D、4个6. 12位参加歌唱比赛的同学的成绩各不相同，按成绩取前6位进入决赛．如果小尹知道了自己的成绩后，要判断自己能否进入决赛，他还要知道这12位同学成绩的（ ）A、平均数 B、众数 C、方差 D、中位数二、填空题
-
7. 如图，在△ABC中，D、E、F分别是AB、BC、CA的中点．若△ABC的面积为3，则的面积为 ．
8. 若式子 在实数范围内有意义，则x的取值范围是.9. 如图，在菱形中，与交于点O，若 ， 则菱形的面积为 ．
10. 直线与直线平行，则k＝ ．11. 若点关于y轴的对称点为 ， 则a+b= ．12. 如图，在菱形ABCD中，点A在x轴上，点B的坐标为（4，1），点D的坐标为（0，1），则点C的坐标为 ．
13. 已知一组数据：2，5，5，6，7，则这组数据的方差是14. 如图，平行四边形中，和的平分线交于E、F两点，则的长是 ．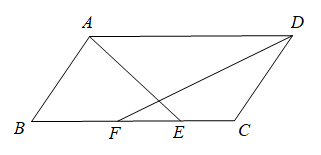
三、解答题
-
15. 先化简，再求值： ， 其中 ．16. 解分式方程： ．17. 为保障新冠病毒抗原检测试剂盒的需求，某生物科技公司开启“加速”模式生产效率比原先提高了20%，现在生产480万试剂盒所用的时间比原先生产450万试剂盒所用的时间少1天．问原先每天生产多少万试剂盒？18. 如图，菱形的对角线相交于点O，垂直平分 ， 垂足为点E，求的大小．
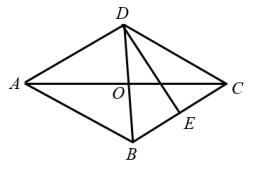19. 如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点B作AC的平行线，两直线相交于点E．
(1)、求证：四边形OBEC是矩形．(2)、若BE=4，BC= ， 则菱形ABCD的面积是 ．20. 等腰三角形的周长是16，求出底边长y与一腰长x的函数关系式，并求出自变量x的取值范围？21. 如图，小颖和她的同学荡秋千，秋千AB在静止位置时，下端B离地面0.6m，荡秋千到AB的位置时，下端B距静止位置的水平距离EB等于2.4m，距地面1.4m，求秋千AB的长.
22. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，点E是AD的中点，过点A作 ， 交BE的延长线于点F，连接CF．
(1)、求证：四边形ADCF是菱形；(2)、若AB＝AC，试判定四边形ADCF的形状．23. 某同学上学期的数学历次测验成绩如下表所示：测试类别
平时测试
期中测试
期末测试
第1次
第2次
第3次
成绩
105
108
110
105
113
(1)、该同学上学期5次测试成绩的众数为 ，中位数为 ．(2)、该同学上学期数学平时成绩的平均数为 ．(3)、该同学上学期的总成绩是将平时测试的平均成绩、期中测试成绩、期末测试成绩按照2：3：5的比例计算所得，求该同学上学期数学学科的总评成绩（结果保留整数）．24. 如图，在矩形ABCD中，AB＝4，AD＝3，连接BD．点P从点A出发，沿折线AB－BD－DC以每秒1个单位长度的速度向终点C运动．以AP为对角线作正方形AEPF（点F在直线AP的右侧）．设正方形AEPF的面积为S（平方单位），点P的运动时间为t（秒）．
(1)、当点P在线段AB上时，求出S与t之间的函数关系式，并写出t的取值范围；(2)、当点P在线段DC上时，求出S与t之间的函数关系式，并写出t的取值范围；(3)、当直线BF将正方形AEPF分成的两部分图形面积相等时，求出t的值．