吉林省2022-2023学年七年级下学期数学期末考试模拟卷（三）

试卷更新日期：2023-06-10 类型：复习试卷

进入出卷网下载

一、单选题

1. 下面各数中，是不等式a＜﹣2的解的是（）

A、﹣3 B、﹣2 C、0 D、1

查看试题解析
2. 若点P是第二象限内的点，且点P到x轴的距离是2，到y轴的距离是3，则点P的坐标是（）

A、(2，3) B、(2，－3) C、(－3，2) D、(3，－2)

查看试题解析
3. 如图，将三角形的直角顶点放在直尺的一边上，若∠1=65°，则∠2的度数为（）

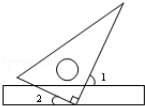A、10° B、15° C、20° D、25°

查看试题解析
4. 下列说法中，错误的是（）

A、4的算术平方根是2 B、 $\sqrt{81}$ 的平方根是±3 C、8的立方根是±2 D、﹣1的立方根等于﹣1

查看试题解析
5. 2022年北京冬奥会顺利闭幕，奥运会吉祥物“冰墩墩”让我们印象深刻，下面是“冰墩墩”的形象图片，在下面的四个图形中，能由图经过平移得到的图形是（）

A、 B、 C、 D、

查看试题解析
6. 在直角坐标系中，点 $P (2 x - 6 ， x - 5)$ 在第四象限，则x的取值范围是（）

A、 $3 < x < 5$ B、 $3 < x < 5$ C、 $- 5 < x < 3$ D、 $- 5 < x < - 3$

查看试题解析

二、填空题

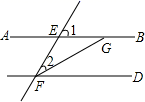
7. 把方程 $2 x + y = 3$ 改写成用含x的式子表示y的形式．

查看试题解析
8. 已知 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ 是二元一次方程 $2 x - k y = - 5$ 的一个解，那么k的值是．

查看试题解析
9. 在平面直角坐标系中，点 $A (- 5 ， 3)$ 到y轴的距离为．

查看试题解析
10. AB∥CD ， ∠1＝58°，FG平分∠EFD ，则∠FGB的度数为．

查看试题解析
11. 已知一个40个数据的样本，把它分成6组，第一组到第四组的频数分别是10、5、7、6，第五组的频率是0.2，那么第六组的频数是．

查看试题解析
12. 如图，AD是△ABC的中线，若AB＝16，AC＝10，则△ABD的周长与△ACD的周长的差为．

查看试题解析
13. 在实数①﹣ $\frac{1}{7}$ ， ② $\sqrt{11}$ ， ③0.3，④ $\frac{π}{3}$ ， ⑤ $\sqrt{36}$ ， ⑥ $\sqrt[3]{- 27}$ ， ⑦0.373737773…（每相邻两个3之间依次多一个7）中，属于无理数的有．

查看试题解析
14. 如图1是我们常用的折叠式小刀，图2中刀柄外形是一个长方形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，若∠1＝52°，则∠2的度数是度．

查看试题解析

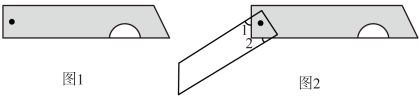
三、解答题

15. 求出下列图形中 $x$ 的值．

查看试题解析
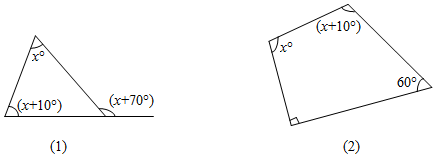16. 如图，AB∥CD，BE平分∠ABC，∠DCB＝140°，求∠ABD和∠EDC的度数．

查看试题解析
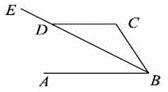17. 如图，先将△ABC向左平移3个单位长度，然后再向下平移4个单位长度，得到△A₁B₁C₁

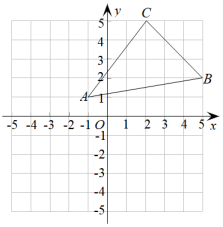(1)、画出经过两次平移后的图形，并写出A₁、B₁、C₁的坐标；

(2)、求ΔABC的面积．

查看试题解析
18. 如图，在△ABC中，点D、E分别在AB、BC 上，且 $D E ∥ A C$ ， ∠1=∠2．求证： $A F ∥ B C$ ；

查看试题解析
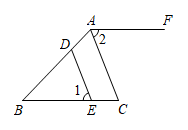19. 已知点P（a﹣2，2a+8），分别根据下列条件求出点P的坐标．

(1)、点P在x轴上；

(2)、点P到x轴、y轴的距离相等．

查看试题解析

20. 在信息快速发展的社会，“信息消费”已成为人们生活的重要部分．泰州市的一个社区随机抽取了部分家庭，调查每月用于信息消费的金额，数据整理成如图所示的不完整统计图．已知A、B两组户数直方图的高度比为1：5，请结合图中相关数据回答下列问题．

月消费额分组统计表

组别	消费金额
A	$10 \leq x < 100$
B	$100 \leq x < 200$
C	$200 \leq x < 300$
D	$300 \leq x < 400$
E	$x ≥ 400$

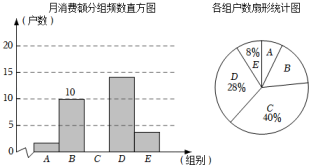(1)、A组的频数是，本次调查样本的容量是；

(2)、补全直方图（需标明各组频数）；

(3)、若该社区有3000户住户，请估计月信息消费额不少于200元的户数是多少？

查看试题解析

21. 在解方程组 ${\begin{matrix} a x + 5 y = 10 \\ 4 x - b y = - 4 \end{matrix}$ 时，由于粗心，甲看错了方程组中的a，得到的解为 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ ，乙看错了方程组中的b，得到的解为 ${\begin{matrix} x = 5 \\ y = 4 \end{matrix}$ ．

(1)、求正确的a，b的值；

(2)、求原方程组的解．

查看试题解析
22. 如图，数轴的正半轴上有A，B，C三点，表示1和 $\sqrt{2}$ 的对应点分别为A，B，点B到点A的距离与点C到原点的距离相等，设点C所表示的数为 $x$ ．

(1)、请你直接写出 $x$ 的值；

(2)、求 $(x - \sqrt{2})^{2}$ 的平方根.

查看试题解析
23. 如图，在平面直角坐标系中，已知：OA＝2，OB＝3．现同时将点A和点B向上平移2个单位长度，再向右平移2个单位长度，分别得到点A和点B的对应点C和D，连接AC，BD，CD．

(1)、直接写出点A，B，C，D的坐标；

(2)、CD＝，S_四_边_形ABDC＝；

(3)、在线段OC上是否存在一点P，使 $S_{△ C D P} ＝ S_{△ O B P}$ ，如果存在，求出点P的坐标；若不存在，说明理由．

查看试题解析
24. 【问题呈现】如图①，△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点．求证：∠P＝ $\frac{1}{2}$ ∠A．

(1)、证明：∵BP、CP分别是∠ABC和∠ACD的角平分线，
∴∠PBC＝ $\frac{1}{2}$ ∠ABC，∠PCD＝ $\frac{1}{2}$   ▲   ，
∵∠PCD＝  ▲  ＋∠P，
∴∠P＝∠PCD﹣  ▲   ，
＝ $\frac{1}{2}$ （∠ACD﹣∠ABC
＝ $\frac{1}{2}$   ▲   ．

(2)、【拓展应用】四边形MBCN中，内角∠ABC与外角∠DCE的平分线所在直线相交而成的锐角记为∠P，设∠A＋∠D＝α．
如图②，若α＝225°，求∠P的度数．

(3)、若α＜180°，请利用图③画图探索，则∠P的大小为度．（用含α的代数式表示）

查看试题解析