人教版八年级下数学期末复习知识点扫盲满分计划——18.1.2三角形的中位线
试卷更新日期:2023-06-10 类型:复习试卷
一、与中位线有关的求解问题
-
1. 如图,在中,交于点E,交于点F,连接交于点M,连接交于点N,连接 . 求证 .
 2. 如图,已知菱形的边长为 , , E为的中点,F为的中点,则的长等于 .
2. 如图,已知菱形的边长为 , , E为的中点,F为的中点,则的长等于 .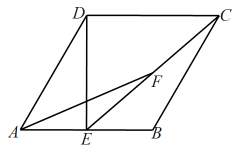 3. 如图,点O为正方形的中心,平分交于点E,延长到点F,使 , 连接交的延长线于点H,连接交于点G,连接.则以下四个结论中:① , ② , ③ , ④ . 正确结论为.
3. 如图,点O为正方形的中心,平分交于点E,延长到点F,使 , 连接交的延长线于点H,连接交于点G,连接.则以下四个结论中:① , ② , ③ , ④ . 正确结论为.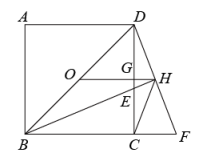 4. 如图,在中, , D、E、F分别是、、的中点.
4. 如图,在中, , D、E、F分别是、、的中点. (1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.5. 如图,在中,已知 , , 平分交边于点E , 点F、G分别是、的中点,则等于( )
(1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.5. 如图,在中,已知 , , 平分交边于点E , 点F、G分别是、的中点,则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、中位线有关的三角形面积问题
-
6. 如图,在中,点分别是的中点,若四边形的面积是 , 则的面积是( )
 A、1 B、2 C、3 D、47. 如图,在平行四边形中,E为的中点,已知的面积为4,则的面积为 .
A、1 B、2 C、3 D、47. 如图,在平行四边形中,E为的中点,已知的面积为4,则的面积为 . 8. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )
8. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )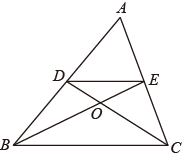 A、6 B、9 C、12 D、13.59. 如图,已知D、E分别是的边、的中点,是的中线,连接、、 , 若的面积为40,则阴影部分的面积为( )
A、6 B、9 C、12 D、13.59. 如图,已知D、E分别是的边、的中点,是的中线,连接、、 , 若的面积为40,则阴影部分的面积为( ) A、10 B、5 C、8 D、410. 如图,在中,点D、E分别是边AB、AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DF交于点O.若的面积为S,则四边形BOGC的面积=
A、10 B、5 C、8 D、410. 如图,在中,点D、E分别是边AB、AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DF交于点O.若的面积为S,则四边形BOGC的面积=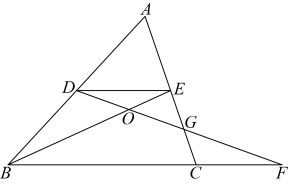
三、三角形中位线有关的证明
-
11. 如图,在△ABC中,D是BC上一点,E、F、G、H分别是BD、BC、AC、AD的中点,求证:EG、HF互相平分.
 12. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
12. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长. 13. 如图,CD是△ABC的中线,E为CD上一点,连接AE并延长至点F,使 ,连接BF,CF,若CF∥AB.求证:四边形DBFC是平行四边形.
13. 如图,CD是△ABC的中线,E为CD上一点,连接AE并延长至点F,使 ,连接BF,CF,若CF∥AB.求证:四边形DBFC是平行四边形.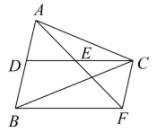 14. 如图,已知等边的边长为4,点D、E分别是、的中点,过点D作 , 交的延长线于点F,求的长.
14. 如图,已知等边的边长为4,点D、E分别是、的中点,过点D作 , 交的延长线于点F,求的长. 15. 如图所示,已知E为▱ABCD中DC边的延长线上的一点,且CE=DC,连结AE,分别交BC,BD于点F,G,连结AC交BD于点O,连结OF。
15. 如图所示,已知E为▱ABCD中DC边的延长线上的一点,且CE=DC,连结AE,分别交BC,BD于点F,G,连结AC交BD于点O,连结OF。求证:AB=2OF。

四、三角形中位线的实际应用
-
16. 如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是m.
 17. 图1是三角形空地,计划用栅栏分成两部分种植不同的植物如图2,则栅栏AB的长度是( )
17. 图1是三角形空地,计划用栅栏分成两部分种植不同的植物如图2,则栅栏AB的长度是( ) A、2m B、3m C、4m D、1m18. 如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若m,则A、B两地的距离是( )
A、2m B、3m C、4m D、1m18. 如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若m,则A、B两地的距离是( ) A、6m B、8m C、9m D、10m19. 东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈养鸡,则需篱笆长米.
A、6m B、8m C、9m D、10m19. 东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈养鸡,则需篱笆长米. 20. 如图,将折叠书架画出侧面示意图,AB面板架,CD为支撑架,EF为锁定杆,F可在CD上移动或固定,已知BC=CE=8cm,如图1,将面板AB竖直固定时(AB⊥BD),点F恰为CD的中点,如图2,当CF=17cm,EF⊥AB,则底部BD=cm,支撑架CD的长度为cm.
20. 如图,将折叠书架画出侧面示意图,AB面板架,CD为支撑架,EF为锁定杆,F可在CD上移动或固定,已知BC=CE=8cm,如图1,将面板AB竖直固定时(AB⊥BD),点F恰为CD的中点,如图2,当CF=17cm,EF⊥AB,则底部BD=cm,支撑架CD的长度为cm.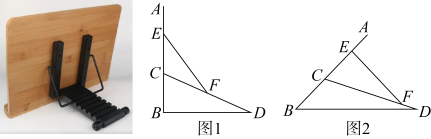
五、综合训练
-
21. 如图,正方形ABCD中,点E,F,G,H分别是各边的中点,连结GH,取GH的中点P,连结EP,FP,则下列说法正确的是( )
 A、PE= GH B、四边形BEPF的周长是△GDH周长的3倍 C、∠EPF=60° D、四边形BEPF的面积是△GDH面积的3倍22. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.
A、PE= GH B、四边形BEPF的周长是△GDH周长的3倍 C、∠EPF=60° D、四边形BEPF的面积是△GDH面积的3倍22. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.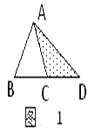

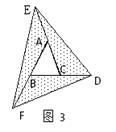

(1)、如图1,延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1 , 则S1=(用含a的代数式表示);
(2)、如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2 , 则S2=(用含a的代数式表示);(3)、在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3 , 则S3=(用含a的代数式表示).发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的倍.
23. 中,D、E分别是 , 的中点,O是内任意一点,连接、 .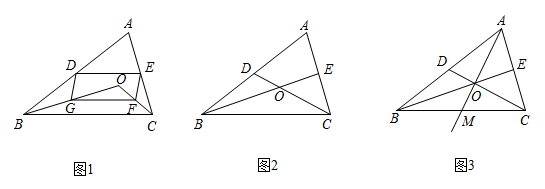 (1)、如图1,点G、F分别是、的中点,连接 , , , , 求证:四边形是平行四边形;(2)、如图2,若点O恰为和交点,求证: , ;(3)、如图3,若点O恰为和交点,射线与交于点M , 求证: .24. 如图,在中, , , , N是BC边上一点,M为AB边上的动点,D,E分别为CN,MN的中点,则DE的最小值是.
(1)、如图1,点G、F分别是、的中点,连接 , , , , 求证:四边形是平行四边形;(2)、如图2,若点O恰为和交点,求证: , ;(3)、如图3,若点O恰为和交点,射线与交于点M , 求证: .24. 如图,在中, , , , N是BC边上一点,M为AB边上的动点,D,E分别为CN,MN的中点,则DE的最小值是.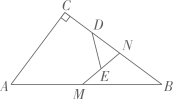 25. 如图,在中, , 延长到 , 使 , 为中点,连接 , 若 , 则 .
25. 如图,在中, , 延长到 , 使 , 为中点,连接 , 若 , 则 . 26. 如图,在△ABC中,BD平分∠ABC交AC于点D,且BD⊥AC,点F在BC上,点E为AF的中点,连接AF ,BE,ED,DF,BF= DE.
26. 如图,在△ABC中,BD平分∠ABC交AC于点D,且BD⊥AC,点F在BC上,点E为AF的中点,连接AF ,BE,ED,DF,BF= DE. (1)、求证:四边形DEBF是平行四边形.(2)、若AC=DE,BD=6,求AB的长.27. 如图1,在中,点D在的延长线上,且 , 分别过点D作交的延长线于点E,连接 , 交于点G,
(1)、求证:四边形DEBF是平行四边形.(2)、若AC=DE,BD=6,求AB的长.27. 如图1,在中,点D在的延长线上,且 , 分别过点D作交的延长线于点E,连接 , 交于点G, (1)、求的长,并证明;(2)、如图1,在射线上只用圆规作一点Q,使得(保留作图痕迹,并简要说明作法);(3)、如图2,在(2)的条件下,连接 , 分别取的中点M、N,动点H在上运动,求的最小值28. 在中,点D和点E分别是上两点,连接.点F、G、H分别是的中点,连接.
(1)、求的长,并证明;(2)、如图1,在射线上只用圆规作一点Q,使得(保留作图痕迹,并简要说明作法);(3)、如图2,在(2)的条件下,连接 , 分别取的中点M、N,动点H在上运动,求的最小值28. 在中,点D和点E分别是上两点,连接.点F、G、H分别是的中点,连接. (1)、猜想与的关系,并证明你的猜想.(2)、若 , , 求的值.29.(1)、【教材呈现】
(1)、猜想与的关系,并证明你的猜想.(2)、若 , , 求的值.29.(1)、【教材呈现】如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
 (2)、【结论应用】
(2)、【结论应用】如图②,在上边题目的条件下,延长图①中的线段的延长线交的延长线于点E,延长线段交的延长线于点F.求证: .
(3)、若(1)中的 , 则的大小为 .30. 如图,是边长为1的等边三角形,取边中点 , 作 , , , 分别交 , 于点 , , 得到四边形 , 它的面积记作;取中点 , 作 , , , 分别交 , 于点 , , 得到四边形 , 它的面积记作……照此规律作下去,则 . 31. 如图,在给定的△ABC中,动点D从点B出发沿BC方向向终点C运动,DEAC交AB于点E,DFAB交AC于点F,O是EF的中点,在整个运动过程中,△OBC的面积的大小变化情况是( )
31. 如图,在给定的△ABC中,动点D从点B出发沿BC方向向终点C运动,DEAC交AB于点E,DFAB交AC于点F,O是EF的中点,在整个运动过程中,△OBC的面积的大小变化情况是( ) A、不变 B、一直增大 C、先增大后减小 D、先减小后增大32. 如图,在△ABC中,AB=20,AC=9,点M为BC的中点,AD平分△ABC的外角∠CAE,交BC延长线于点D,过点M作MN∥AD,交AB于点N,则AN的长为 .
A、不变 B、一直增大 C、先增大后减小 D、先减小后增大32. 如图,在△ABC中,AB=20,AC=9,点M为BC的中点,AD平分△ABC的外角∠CAE,交BC延长线于点D,过点M作MN∥AD,交AB于点N,则AN的长为 . 33. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )
33. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )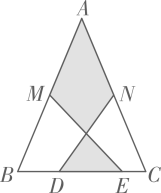 A、25cm2 B、35cm2 C、30cm2 D、42cm234. 如图,将△ABC沿着它的中位线DE对折,点A落在F处.若∠C=120°,∠A=20°,则∠FEB的度数是( )
A、25cm2 B、35cm2 C、30cm2 D、42cm234. 如图,将△ABC沿着它的中位线DE对折,点A落在F处.若∠C=120°,∠A=20°,则∠FEB的度数是( ) A、140° B、120° C、100° D、80°35. 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.如图1,小明在证明这个定理时,通过延长DE到点F,使EF=DE,连接CF,证明△ADE△CFE,再证明四边形DBCF是平行四边形,即可得证.
A、140° B、120° C、100° D、80°35. 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.如图1,小明在证明这个定理时,通过延长DE到点F,使EF=DE,连接CF,证明△ADE△CFE,再证明四边形DBCF是平行四边形,即可得证.
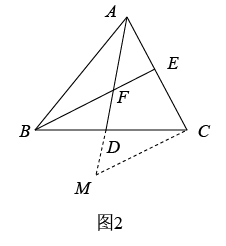

 (1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.
(1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.小明发现可以类比以上思路进行证明.
证明:如图2,延长AD至点M,使MD=FD,连接MC,……
请你根据小明的思路完成证明过程.
(2)、【方法运用】如图3,在菱形ABCD中,∠D=60°,点E为射线BC上一个动点(在点C右侧),把线段EC绕点E逆时针旋转120°得到线段BC′,连接BC′,点F是BC′的中点,连接AE、CF、EF.①请你判断线段EF和AE的数量关系是 ▲ , 并说明理由;
②若菱形ABCD的边长为6,CF=CE,请直接写出CF的长.
36. 如图,已知∠AED=∠ACB=90°,AC=BC=3,AE=DE=1,点D在AB上,连接CE,点M,点N分别为BD,CE的中点,则MN的长为 . 37. 如图,在中, , , 点D、E分别在边AB、AC上, , , 取DE、BC的中点M、N,线段MN的长为( )
37. 如图,在中, , , 点D、E分别在边AB、AC上, , , 取DE、BC的中点M、N,线段MN的长为( )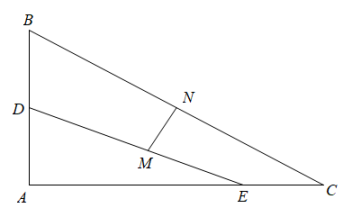 A、2.5 B、3 C、4 D、538. 如图,在中,E,F分别是的中点, , 垂足为H,与交于点G,若 , 则的长为 .
A、2.5 B、3 C、4 D、538. 如图,在中,E,F分别是的中点, , 垂足为H,与交于点G,若 , 则的长为 . 39. 如图直角坐标系中直线AB与x轴正半轴、y轴正半轴交于A,B两点,已知B(0,4),∠BAO=30°,P,Q分别是线段OB,AB上的两个动点,P从O出发以每秒3个单位长度的速度向终点B运动,Q从B出发以每秒8个单位长度的速度向终点A运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t(秒).
39. 如图直角坐标系中直线AB与x轴正半轴、y轴正半轴交于A,B两点,已知B(0,4),∠BAO=30°,P,Q分别是线段OB,AB上的两个动点,P从O出发以每秒3个单位长度的速度向终点B运动,Q从B出发以每秒8个单位长度的速度向终点A运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t(秒). (1)、求线段AB的长,及点A的坐标;
(1)、求线段AB的长,及点A的坐标;
(2)、t为何值时,△BPQ的面积为2 ;(3)、若C为OA的中点,连接QC,QP,以QC,QP为邻边作平行四边形PQCD,①t为何值时,点D恰好落在坐标轴上;
②是否存在时间t使x轴恰好将平行四边形PQCD的面积分成1:3的两部分,若存在,直接写出t的值.
40. 如图,在平行四边形中,对角线、相交于点, , 是边的中点,、为上的点,连接和 , 若 , , , 则图中阴影部分的面积为.