人教版八年级下数学期末复习知识点扫盲满分计划——18.1.2平行四边形的判定一
试卷更新日期:2023-06-10 类型:复习试卷
一、判断能否构成平行四边形
-
1. 不能判定四边形为平行四边形的题设是( )
 A、 , B、 , C、 , D、 ,2. 不能判定四边形ABCD为平行四边形的题设是( )A、AB=CD,AB∥CD B、∠A=∠C,∠B=∠D C、AB=AD,BC=CD D、AB=CD,AD=BC3. 如图,四边形ABCD的两条对角线AC、BD交于点O,下列条件不能判定四边形ABCD是平行四边形的是( )
A、 , B、 , C、 , D、 ,2. 不能判定四边形ABCD为平行四边形的题设是( )A、AB=CD,AB∥CD B、∠A=∠C,∠B=∠D C、AB=AD,BC=CD D、AB=CD,AD=BC3. 如图,四边形ABCD的两条对角线AC、BD交于点O,下列条件不能判定四边形ABCD是平行四边形的是( ) A、AO=CO,BO=DO B、AB=CD,AD=BC C、AB∥CD,AB=CD D、AB∥CD,AD=BC4. 下列条件中,不能判定四边形是平行四边形的条件是( )A、两组对边分别平行 B、两组对边分别相等 C、一组对边平行,另一组对边相等 D、一组对边平行且相等5. 下列条件中,能判定一个四边形为平行四边形的是( )A、一组对边相等 B、一组对边平行,另一组对边相等 C、两条对角线互相垂直 D、两组对边分别相等
A、AO=CO,BO=DO B、AB=CD,AD=BC C、AB∥CD,AB=CD D、AB∥CD,AD=BC4. 下列条件中,不能判定四边形是平行四边形的条件是( )A、两组对边分别平行 B、两组对边分别相等 C、一组对边平行,另一组对边相等 D、一组对边平行且相等5. 下列条件中,能判定一个四边形为平行四边形的是( )A、一组对边相等 B、一组对边平行,另一组对边相等 C、两条对角线互相垂直 D、两组对边分别相等二、添加一个条件成为平行四边形
-
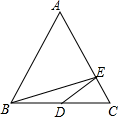
6. 如图,在中, , 分别是 , 上的点,请添加一个条件,使得四边形为平行四边形,则添加的条件是(答案不唯一).
 7. 如图,平行四边形中, , 是对角线上的两点,如果添加一个条件使四边形是平行四边形,则添加的条件不能是( )
7. 如图,平行四边形中, , 是对角线上的两点,如果添加一个条件使四边形是平行四边形,则添加的条件不能是( ) A、 B、 C、 D、8. 如图,在▱ABCD中,E,F是对角线BD上的两点,要使四边形AFCE是平行四边形,则需添加的一个条件可以是 . (只添加一个条件)
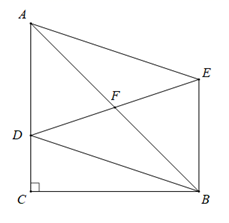
A、 B、 C、 D、8. 如图,在▱ABCD中,E,F是对角线BD上的两点,要使四边形AFCE是平行四边形,则需添加的一个条件可以是 . (只添加一个条件) 9. 如图,在四边形中, , , 垂足分别为点E,F.请你只添加一个条件(不另加辅助线),使得四边形为平行四边形,你添加的条件是 .
9. 如图,在四边形中, , , 垂足分别为点E,F.请你只添加一个条件(不另加辅助线),使得四边形为平行四边形,你添加的条件是 . 10. 在中,点D,E分别是 , 上的点,且 , 点F是延长线上一点,连接 . 添加下列条件后,不能判断四边形是平行四边形的是( )
10. 在中,点D,E分别是 , 上的点,且 , 点F是延长线上一点,连接 . 添加下列条件后,不能判断四边形是平行四边形的是( ) A、 B、 C、 D、
A、 B、 C、 D、三、数形中平行四边形的个数
-
11. 如图,在平行四边形中,与相交于点 , 图中共有个平行四边形( )
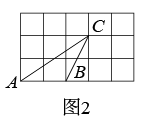
 A、4个 B、5个 C、8个 D、9个12. 如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有个.
A、4个 B、5个 C、8个 D、9个12. 如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有个. 13. 如图,我们称四个顶点都恰好在格点的四边形为格点四边形,A,B为4×4的正方形网格中的两个格点,在此图中以A,B为顶点的格点四边形是平行四边形的个数是( ).
13. 如图,我们称四个顶点都恰好在格点的四边形为格点四边形,A,B为4×4的正方形网格中的两个格点,在此图中以A,B为顶点的格点四边形是平行四边形的个数是( ). A、10 B、11 C、12 D、1314. 如图所示,在▱ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,则图中共有个平行四边形.
A、10 B、11 C、12 D、1314. 如图所示,在▱ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,则图中共有个平行四边形. 15. 如图,在图1中,A1 , B1 , C1分别是△ABC的边BC,CA,AB的中点,在图2中,A2 , B2 , C2分别是△A1B1C1的边B1C1 , C1A1 , A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有个.
15. 如图,在图1中,A1 , B1 , C1分别是△ABC的边BC,CA,AB的中点,在图2中,A2 , B2 , C2分别是△A1B1C1的边B1C1 , C1A1 , A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有个.
四、求已知三点平行四边形的个数
-
16. 在平面直角坐标系中,以 , , 为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )A、 B、 C、 D、17. 如图在10×10的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
 (1)、计算AC,AB,BC的长度,并判定△ABC 的形状;(2)、若在网格所在的坐标平面内的点A,C的坐标分别为(0,0),(-1,1).请你在图中找出点D,使以A、B、C、D四个点为顶点的四边形是平行四边形,直接写出满足条件的D点的坐标.18. 在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1),为顶点构造平行四边形,下列各点中不能作为平行四边形第四个顶点的坐标的是( )
(1)、计算AC,AB,BC的长度,并判定△ABC 的形状;(2)、若在网格所在的坐标平面内的点A,C的坐标分别为(0,0),(-1,1).请你在图中找出点D,使以A、B、C、D四个点为顶点的四边形是平行四边形,直接写出满足条件的D点的坐标.18. 在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1),为顶点构造平行四边形,下列各点中不能作为平行四边形第四个顶点的坐标的是( )
 A、 B、 C、 D、19. 如图,在的正方形网格中,每个小格的顶点叫做格点,点 , , 均在格点上,按下列要求画图.
A、 B、 C、 D、19. 如图,在的正方形网格中,每个小格的顶点叫做格点,点 , , 均在格点上,按下列要求画图.
 (1)、在图1中,画出一个 , 使顶点在格点上;(2)、在图2中,画出一条线段 , 使 , 且点在格点上.20. 如图,在边长为1个单位长度的小正方形组成的网格中,每个小正方形的顶点叫做格点,其中点A,B,C都在格点上,点M是线段AB的中点.
(1)、在图1中,画出一个 , 使顶点在格点上;(2)、在图2中,画出一条线段 , 使 , 且点在格点上.20. 如图,在边长为1个单位长度的小正方形组成的网格中,每个小正方形的顶点叫做格点,其中点A,B,C都在格点上,点M是线段AB的中点.
( 1 )请在网格中画出以AB、BC为邻边的平行四边形ABCD;
( 2 )利用网格图,画出直线MN,使 .
五、证明四边形是平行四边形
-
21.
如图,已知□ABCD的对角线AC , BD相交于点O , 直线EF经过点O , 且分别交AB , CD于点E , F.求证:四边形BFDE是平行四边形.
 22. 如图,在平行四边形 中,E、F是对角线上的两点,且. 求证:四边形是平行四边形.
22. 如图,在平行四边形 中,E、F是对角线上的两点,且. 求证:四边形是平行四边形. 23. 如图,在▱中, , 是AB,上的点,且 , 求证:四边形是平行四边形.
23. 如图,在▱中, , 是AB,上的点,且 , 求证:四边形是平行四边形. 24. 如图,在平行四边形ABCD中,DF=BE.求证:四边形AECF是平行四边形.
24. 如图,在平行四边形ABCD中,DF=BE.求证:四边形AECF是平行四边形. 25. 如图,已知平行四边形ABCD中,点E为BC边的中点,连DE并延长DE交AB延长线于点F,求证:四边形DBFC是平行四边形.
25. 如图,已知平行四边形ABCD中,点E为BC边的中点,连DE并延长DE交AB延长线于点F,求证:四边形DBFC是平行四边形.
六、全等三角形拼成平行四边形问题
-
26. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
已知:如图,中,D、E分别是的中点.
求证:∥ , 且 .

方法一
证明:如图,延长至点F,使 , 连接 .

方法二
证明:如图,过点C作∥交的延长线于F.
 27. 如图,以▱ABCD的边AD、BC为边向外作等边三角形ADE和BCF,连接CE、AF,求证:四边形AECF是平行四边形.
27. 如图,以▱ABCD的边AD、BC为边向外作等边三角形ADE和BCF,连接CE、AF,求证:四边形AECF是平行四边形. 28. 如图,是等边三角形,是射线上的一个动点(点不与 , 重合),是以为边的等边三角形,过点作的平行线交射线于点 , 连接 .
28. 如图,是等边三角形,是射线上的一个动点(点不与 , 重合),是以为边的等边三角形,过点作的平行线交射线于点 , 连接 . (1)、如图1,点在线段上时,求证:;(2)、请判断图1中四边形的形状,并说明理由;(3)、若点在边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.29. 问题提出:一条线段沿某个方向平移一段距离后与原线段构成一个平行四边形.我们可以利用这一性质,将有些条件通过平移集中在一起来解决一些几何问题.
(1)、如图1,点在线段上时,求证:;(2)、请判断图1中四边形的形状,并说明理由;(3)、若点在边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.29. 问题提出:一条线段沿某个方向平移一段距离后与原线段构成一个平行四边形.我们可以利用这一性质,将有些条件通过平移集中在一起来解决一些几何问题.
如图①,两条长度相等的线段和相交于O点, , 直线与直线的夹角为 , 求线段、、满足的数量关系.
分析:考虑将、和集中到同一个三角形中,以便运用三角形的知识寻求三条线段的数量关系:
如图②,作且 , 则四边形是平行四边形,从而;
由于 , , 所以是等边三角形,故;
通过平行又求得.
在中,研究三条线段的大小关系就可以了.
(1)、如图②,若 , , , 请直接写出线段的长;(2)、问题解决:如图③,矩形中,E、F分别是、上的点,满足 , , 求证:;(3)、拓展应用:如图④,中, , D、E分别在、上,、交于点O, , , 若 , , 则.30. 如图,已知是等边三角形,E为AC上一点,连接BE.将旋转,使得点C落在BC上的点D处,点B落在BC上方的点F处,旋转后的三角形是 , 连接AF.请证明:四边形ABDF是平行四边形.
七、利用平行四边形的判定和性质求解
-
31. 如图,O是等边三角形ABC内任意一点,过点O作OD∥AB,OE∥AC,OF∥BC分别交AC,BC,AB于点G,H,I,已知等边三角形ABC的周长18,则OD+OE+OF= 。
 32. 如图,已知是边长为的等边三角形,点D是边上的一点,且 , 以为边作等边 , 过点E作EF//BC,交于点F,连接 , 则
32. 如图,已知是边长为的等边三角形,点D是边上的一点,且 , 以为边作等边 , 过点E作EF//BC,交于点F,连接 , 则.
 33. 如图,直角三角形 中, , 于点 , 平分 交 于点 ,交 于点 , 交 于点 , 于 ,以下4个结论:① ;② 是等边三角形;③ ;④ 中正确的是(将正确结论的序号填空)
33. 如图,直角三角形 中, , 于点 , 平分 交 于点 ,交 于点 , 交 于点 , 于 ,以下4个结论:① ;② 是等边三角形;③ ;④ 中正确的是(将正确结论的序号填空)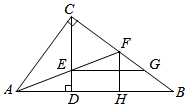 34. 如图,D,E分别是三角形ABC边AB,BC上的点,DE∥AC,点F在DE的延长线上,且∠DFC=∠A.
34. 如图,D,E分别是三角形ABC边AB,BC上的点,DE∥AC,点F在DE的延长线上,且∠DFC=∠A. (1)、求证:四边形ADFC是平行四边形;(2)、若∠ACF比∠BDE大40°,求∠BDE的度数.
(1)、求证:四边形ADFC是平行四边形;(2)、若∠ACF比∠BDE大40°,求∠BDE的度数.八、平行四边形性质与判定的应用
-
35. 【问题背景】
某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作于点F,请写出线段、、之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作 , 交的延长线于点H;
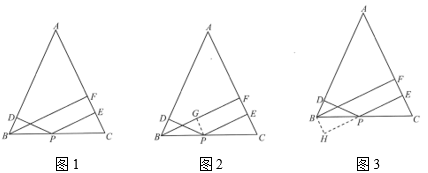
 (1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】
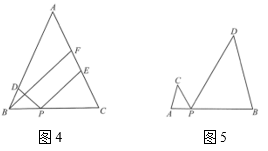
(1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】如图4,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作交于点F,请写出线段之间满足的数量关系式,并说明理由.
(3)、 【拓展应用】如图5,在与中, , , 点A、B、P在同一条直线上,若 , , 则 .
36. 如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F. (1)、若点D是BC边的中点(如图①),求证:EF=CD;(2)、在(1)的条件下直接写出△AEF和△ABC的面积比;(3)、若点D是BC边上的任意一点(除B、C外如图②),那么(1)中的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.37. 已知如图,D是△ABC中AB边上的中点,△ACE和△BCF分别是以AC、BC为斜边的等腰直角三角形,连接DE、DF.
(1)、若点D是BC边的中点(如图①),求证:EF=CD;(2)、在(1)的条件下直接写出△AEF和△ABC的面积比;(3)、若点D是BC边上的任意一点(除B、C外如图②),那么(1)中的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.37. 已知如图,D是△ABC中AB边上的中点,△ACE和△BCF分别是以AC、BC为斜边的等腰直角三角形,连接DE、DF.求证:DE=DF.
 38.
38.已知:在△ABC中,AB=AC,AD⊥BC,垂足为点D,E在CB的延长线上,且BE=2BD,连接AE,F是AC的中点,G是AE的中点,连接BG、BF.
(1)如图1,求证:四边形AGBF是平行四边形.
(2)如图2,连接GF、DF,GF与AB相交于点H,若GF=AB,在不添加任何辅助线的情况下,请直接写出图2中所有的等边三角形.