沪科版七年级下册10.3平行线的判定及性质专题练习
试卷更新日期:2023-06-10 类型:同步测试
一、解答题
-
1. 如图,于 , 于 , // , . 求证: .
 2. 看图填写.
2. 看图填写.已知:如图, , , . 求证:平分 .

证明:∵ , ,
∴ , . ( )(填推理依据)
∴ .
∴ . ( )(填推理依据)
∴ . ( )(填推理依据)
. ( )(填推理依据)
又∵ , ∴ .
∴平分 . ( )(填推理依据)
3. 推理填空:已知:如图 , , , 求证: .
证明:∵ , (已知),
∴ ,
∴ ▲ , ( )
又∵ , (已知)
∴ ▲ , ( )
∴ ▲ , ( )
∴ , ( )
 4. 已知:如图,与互补, , 试说明 .
4. 已知:如图,与互补, , 试说明 .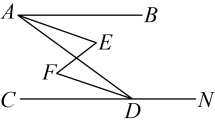
解:因为与互补
所以( )
所以( )
又因为( )
所以 (等式性质)
即
所以( )
所以( )
5. 如图,已知于点 , 于点 , , 求证: .请完成下面的证明及理由填写.

证明:∵(已知),
∴(垂直的定义),
∵(已知),
∴( ),
∴(等量代换)
∴( ).
∴( )
又∵(已知),
∴ ▲ ( )
∴( )
∴( )
6. 阅读理解,补全证明过程及推理依据.已知:如图,点在直线上,点在直线上, , . 求证: .

证明:∵(已知)
( )
∴(等量代换)
∴( )
∴ ▲ (两直线平行,同旁内角互补)
又∵(已知)
∴ ▲ (等量代换)
∴ ▲ ▲ ( )
∴( )
7. 如图,直线与相交于点 , , , , 求证:.
证明:已知 ,
( )
已知 ,
▲ ( )
已知 ,
( )
即 ▲ .
▲ ( )
( )
8. 推理填空:如图,于 , 于 , , 可得平分.

理由如下:于 , 于 , (已知)
, (垂直的定义)
, ( )
▲ , ( )
, ( )
又 , (已知)
▲ , (等量代换)
平分(角平分线的定义)
9. 完成下面的证明:已知:如图, , .
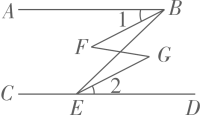
求证:.
证明:∵(已知),
∴ ▲ // ▲ ( ).
∴( ).
又∵(已知),
∴( ).
即.
∴ ▲ // ▲ ( ).
∴(两直线平行,内错角相等).
10. 如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B. 11. 已知:如图,BD⊥AC于点D,EF⊥AC于点F,∠1+∠2=180°.求证:DGBC.
11. 已知:如图,BD⊥AC于点D,EF⊥AC于点F,∠1+∠2=180°.求证:DGBC. 12. 如图,在和中, , , , 与相交于点 , 若 , 请判断与是否平行?并说明理由.
12. 如图,在和中, , , , 与相交于点 , 若 , 请判断与是否平行?并说明理由.
二、综合题
-
13. 如图,已知 , 于点 , .
 (1)、求证:;(2)、连接 , 若 , 且 , 求的度数.14. 如图,∠AGB=∠EHF,∠C=∠D,
(1)、求证:;(2)、连接 , 若 , 且 , 求的度数.14. 如图,∠AGB=∠EHF,∠C=∠D,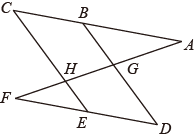 (1)、求证:BDCE;(2)、若∠A=30°,求∠F的度数.15. 如图,已知线段 , 分别以点A,B为端点作射线 , C,D,E三点分别在上,过点C的直线与线段分别交于点F,H,已知 , .
(1)、求证:BDCE;(2)、若∠A=30°,求∠F的度数.15. 如图,已知线段 , 分别以点A,B为端点作射线 , C,D,E三点分别在上,过点C的直线与线段分别交于点F,H,已知 , . (1)、判断与的位置关系并加以证明;(2)、若 , , 求的度数.16. 如图,已知 , .
(1)、判断与的位置关系并加以证明;(2)、若 , , 求的度数.16. 如图,已知 , . (1)、证明:;(2)、若 , , 求的度数.17. 如图,在△ABC中,∠A=∠ABC,直线EF分别交AB、AC和CB的延长线于点D、E、F,过点B作BP//AC交EF于点P.
(1)、证明:;(2)、若 , , 求的度数.17. 如图,在△ABC中,∠A=∠ABC,直线EF分别交AB、AC和CB的延长线于点D、E、F,过点B作BP//AC交EF于点P. (1)、若∠A=70°,∠F=25°,求∠BPD的度数.(2)、求证:∠F+∠FEC=2∠ABP.18. 如图,在中,点D在边上, , 分别交、于点E、F,平分 , 交于点G,
(1)、若∠A=70°,∠F=25°,求∠BPD的度数.(2)、求证:∠F+∠FEC=2∠ABP.18. 如图,在中,点D在边上, , 分别交、于点E、F,平分 , 交于点G,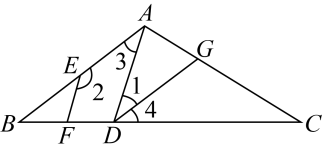 (1)、求证:;(2)、若 , 求的度数.19. 已知:直线 , 点P在的上方,且 , .(1)、如图,求的度数;
(1)、求证:;(2)、若 , 求的度数.19. 已知:直线 , 点P在的上方,且 , .(1)、如图,求的度数; (2)、如图,若的平分线和的平分线交于点G,求的度数.
(2)、如图,若的平分线和的平分线交于点G,求的度数. 20. 如图,直线 , 点E,G在直线AB上,点F,H在直线CD上,∠1+∠2=180°.
20. 如图,直线 , 点E,G在直线AB上,点F,H在直线CD上,∠1+∠2=180°.
 (1)、如图1,求证:;(2)、如图2,若∠1=120°,GM平分∠BGH,FM平分∠EFH,设FM与GH相交于点O.求∠FOH的度数.21. 综合与实践课上,同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a,b且ab,三角形ABC中,∠ACB=90°,∠ABC=60° ∠BAC=30°.操作发现:
(1)、如图1,求证:;(2)、如图2,若∠1=120°,GM平分∠BGH,FM平分∠EFH,设FM与GH相交于点O.求∠FOH的度数.21. 综合与实践课上,同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a,b且ab,三角形ABC中,∠ACB=90°,∠ABC=60° ∠BAC=30°.操作发现: (1)、如图1,若∠1=42°,求∠2的度数;(2)、小聪同学把图1中的直线a向上平移得到如图2,请你探究图2中的∠1与∠2的数量关系,并说明理由.(3)、小颖同学将图2中的直线b向上平移得到图3,若∠2=4∠1,求∠1的度数.22. 丁丁学习七年级下册数学后,遇到了一些问题,请你帮他解决一下.
(1)、如图1,若∠1=42°,求∠2的度数;(2)、小聪同学把图1中的直线a向上平移得到如图2,请你探究图2中的∠1与∠2的数量关系,并说明理由.(3)、小颖同学将图2中的直线b向上平移得到图3,若∠2=4∠1,求∠1的度数.22. 丁丁学习七年级下册数学后,遇到了一些问题,请你帮他解决一下. (1)、如图1,已知ABCD,点E在两平行线的内侧,连接AE,CE.若∠EAB=35°,∠ECD=25°,求∠AEC的度数;(提示:过点E作AB的平行线)(2)、如图2,已知ABCD,点E在两平行线的外侧,连接AE,CE.若∠EAB=α,∠ECD=β.
(1)、如图1,已知ABCD,点E在两平行线的内侧,连接AE,CE.若∠EAB=35°,∠ECD=25°,求∠AEC的度数;(提示:过点E作AB的平行线)(2)、如图2,已知ABCD,点E在两平行线的外侧,连接AE,CE.若∠EAB=α,∠ECD=β.①求∠AEC的大小(用含α,β的代数式表示);
②作∠ECD的平分线交AB于点G,连接GE,AG平分于∠CGE(如图3).若∠AEG=130°,α+β=80°,分别求出α,β的度数.
23. 如图1,已知 , 点 , 分别在射线和上,在内部作射线 , , 使平行于 . (1)、如图1,若 , 求的度数;(2)、小颖发现,在内部,无论如何变化,的值始终为定值,请你结合图2求出这一定值;(3)、①如图3,把图1中的改为 , 其他条件不变,请直接写出与之间的数量关系;
(1)、如图1,若 , 求的度数;(2)、小颖发现,在内部,无论如何变化,的值始终为定值,请你结合图2求出这一定值;(3)、①如图3,把图1中的改为 , 其他条件不变,请直接写出与之间的数量关系;②如图4,已知 , 点 , 分别在射线 , 上,在与内部作射线 , , 使平行于 , 请直接写出与之间的数量关系.
24. 如图,直线 , 直线与 , 分别交于点 , , .小安将一个含角的直角三角板按如图①放置,使点、分别在直线、上,且在点、的右侧, , .

 (1)、填空; (填“”“ ”或“=” );(2)、若的平分线交直线于点 , 如图②.
(1)、填空; (填“”“ ”或“=” );(2)、若的平分线交直线于点 , 如图②.①当 , 时,求的度数;
②小安将三角板沿直线左右移动,保持 , 点、分别在直线和直线上移动,请直接写出的度数(用含的式子表示).
25. 如图,已知直线. (1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当秒时,.
(1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当秒时,.