广东省广州市增城区2023年中考数学二模试卷
试卷更新日期:2023-06-08 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。)
-
1. 如图所示的几何体的主视图是( )
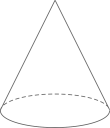 A、
A、 B、
B、 C、
C、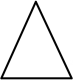 D、
D、 2. 若分式有意义,则的取值范围是( )A、 B、 C、 D、3. 点关于原点对称的点为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,是的直径,弦于点 , , , 则( )
2. 若分式有意义,则的取值范围是( )A、 B、 C、 D、3. 点关于原点对称的点为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,是的直径,弦于点 , , , 则( ) A、5 B、4 C、3 D、26. 如图,在中, , , 则的长是( )
A、5 B、4 C、3 D、26. 如图,在中, , , 则的长是( ) A、6 B、7 C、8 D、97. 九章算术是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:把一份文件送到900里外的城市,用慢马送所需的时间比用快马送所需的时间多4天已知快马速度是慢马速度的2倍,求慢马的速度设慢马的速度为里天,则可列方程为(A、 B、 C、 D、8. 如图,点是函数图象上一点,过点作轴,轴,分别与函数的图象相交于点和点 , 则的面积是( )A、4 B、 C、6 D、9. 如图,点 , 都是边上的点, , 交于点 , 若 , 则:的值是( )
A、6 B、7 C、8 D、97. 九章算术是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:把一份文件送到900里外的城市,用慢马送所需的时间比用快马送所需的时间多4天已知快马速度是慢马速度的2倍,求慢马的速度设慢马的速度为里天,则可列方程为(A、 B、 C、 D、8. 如图,点是函数图象上一点,过点作轴,轴,分别与函数的图象相交于点和点 , 则的面积是( )A、4 B、 C、6 D、9. 如图,点 , 都是边上的点, , 交于点 , 若 , 则:的值是( )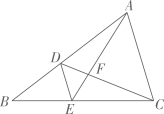 A、1:5 B、1:4 C、1:3 D、1:210. 如图,平面直角坐标系中,已知 , , , 抛物线过点、 , 顶点为 , 抛物线过点 , , 顶点为 , 若点在线段上,则:的值为( )
A、1:5 B、1:4 C、1:3 D、1:210. 如图,平面直角坐标系中,已知 , , , 抛物线过点、 , 顶点为 , 抛物线过点 , , 顶点为 , 若点在线段上,则:的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
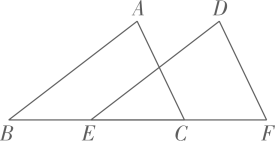
11. 计算 =.12. 如图,在中, , 将沿着射线平移个单位长度,得到 , 若 , 则 .
 13. 如表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差:
13. 如表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差:甲
乙
丙
平均数
9.23
9.3
9.3
方差
0.23
0.017
0.057
根据表中的数据,要选择一名成绩好且发挥稳定的学生参加比赛,应选择 .
14. 抛物线的对称轴是直线 .15. 如图,直线与轴和轴分别交于、两点,射线于点 , 若点是射线上的一个动点,点是轴上的一个动点,且以 , , 为顶点的三角形与全等,则的长为 . 16. 如图,在菱形中, , , 点为对角线不含点上任意一点,则的最小值为 .
16. 如图,在菱形中, , , 点为对角线不含点上任意一点,则的最小值为 .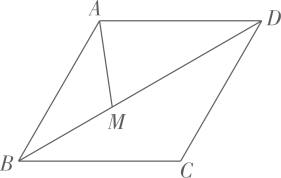
三、解答题(本大题共9小题,共72.0分。)
-
17. 解方程: .18. 如图, , , , 求的长.
 19. 已知 .(1)、化简;(2)、若点在一次函数的图象上,求的值.20. 新课标(2022年版要求学校教育要坚持“立德树人”,实施“跨学科学习、项目式学习”我区九年级学生进行了一次数学素养监测,并随机抽取了名学生的测试成绩,按照“优”“良”“中”“差”四个等级进行统计,并根据统计结果绘制成了如下两幅不完整的统计图.
19. 已知 .(1)、化简;(2)、若点在一次函数的图象上,求的值.20. 新课标(2022年版要求学校教育要坚持“立德树人”,实施“跨学科学习、项目式学习”我区九年级学生进行了一次数学素养监测,并随机抽取了名学生的测试成绩,按照“优”“良”“中”“差”四个等级进行统计,并根据统计结果绘制成了如下两幅不完整的统计图.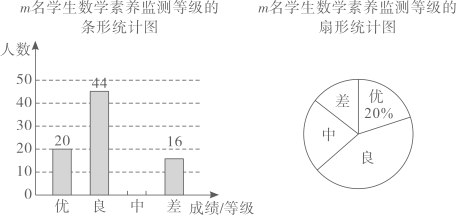 (1)、求的值;(2)、将条形统计图补充完整;(3)、现从成绩为“优”的甲、乙、丙、丁四位同学中随机抽取两位同学参与“跨学科学习、项目式学习”汇报,用树状图或列表法求出甲同学被抽到的概率.21. 如图,矩形中,点是对角线的中点, , , 若反比例函数的图象经过点 , 与边交于点 .
(1)、求的值;(2)、将条形统计图补充完整;(3)、现从成绩为“优”的甲、乙、丙、丁四位同学中随机抽取两位同学参与“跨学科学习、项目式学习”汇报,用树状图或列表法求出甲同学被抽到的概率.21. 如图,矩形中,点是对角线的中点, , , 若反比例函数的图象经过点 , 与边交于点 . (1)、求的值;(2)、求的面积.22. 随着我国数字化阅读方式的接触率和人群持续增多,数字阅读凭借独有的便利性成为了更快获得优质内容的重要途径某市2020年数字阅读市场规模为400万元,2022年数字阅读市场规模为576万元.(1)、求2020年到2022年该市数字阅读市场规模的年平均增长率;(2)、若年平均增长率不变,求2023年该市数字阅读市场规模是多少万元?23. 如图,在等腰中, , 过点作交于点 .
(1)、求的值;(2)、求的面积.22. 随着我国数字化阅读方式的接触率和人群持续增多,数字阅读凭借独有的便利性成为了更快获得优质内容的重要途径某市2020年数字阅读市场规模为400万元,2022年数字阅读市场规模为576万元.(1)、求2020年到2022年该市数字阅读市场规模的年平均增长率;(2)、若年平均增长率不变,求2023年该市数字阅读市场规模是多少万元?23. 如图,在等腰中, , 过点作交于点 .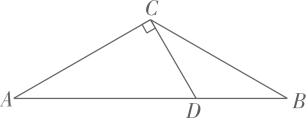 (1)、尺规作图:作的垂直平分线,交于点 , 以点为圆心,为半径作保留痕迹,不要求写作法;(2)、在(1)所作的图形中,
(1)、尺规作图:作的垂直平分线,交于点 , 以点为圆心,为半径作保留痕迹,不要求写作法;(2)、在(1)所作的图形中,求证:是的切线;
若的半径为 , 问线段上是否存在一点 , 使得以 , , 为顶点的三角形与相似?若存在,求出的长;若不存在,请说明理由.
