广东省广州市部分地区2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-06-08 类型:期中考试
一、选择题(本题有10个小题,每小题3分,满分30分.)
-
1. 下列各数中,无理数是( )A、 B、2.23 C、 D、2. 下列各图中,∠1与∠2是对顶角的是( )A、
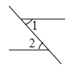 B、
B、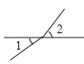 C、
C、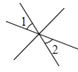 D、
D、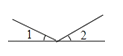 3. 点A(1,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列图形中,不能通过其中一个四边形平移得到的是( )A、
3. 点A(1,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列图形中,不能通过其中一个四边形平移得到的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,若m∥n,∠1=100°,则∠2=( )
5. 如图,若m∥n,∠1=100°,则∠2=( ) A、65° B、70° C、75° D、80°6. 如图,用方向和距离描述少年宫相对于小明家的位置,正确的是( )
A、65° B、70° C、75° D、80°6. 如图,用方向和距离描述少年宫相对于小明家的位置,正确的是( )
 A、北偏东55°,2km B、东北方向 C、东偏北35°,2km D、北偏东35°,2km7. 下列命题中,是真命题的是( )A、邻补角是互补的角 B、两个锐角的和是锐角 C、相等的角是对顶角 D、同旁内角互补8. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A、北偏东55°,2km B、东北方向 C、东偏北35°,2km D、北偏东35°,2km7. 下列命题中,是真命题的是( )A、邻补角是互补的角 B、两个锐角的和是锐角 C、相等的角是对顶角 D、同旁内角互补8. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )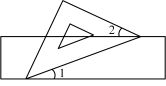 A、30° B、25° C、20° D、15°9. 如图:已知AB⊥BC,垂足为B,AB=3.5,点P是射线BC上的动点,则线段AP的长不可能是( )
A、30° B、25° C、20° D、15°9. 如图:已知AB⊥BC,垂足为B,AB=3.5,点P是射线BC上的动点,则线段AP的长不可能是( )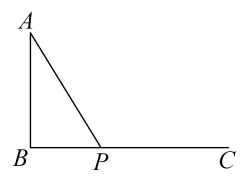 A、3 B、3.5 C、4 D、510. 如图所示,平面直角坐标系中,x轴负半轴上有一点A(-1,0),点A第1次向上平移1个单位至点A1(-1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2023时,点A2023的坐标是( )
A、3 B、3.5 C、4 D、510. 如图所示,平面直角坐标系中,x轴负半轴上有一点A(-1,0),点A第1次向上平移1个单位至点A1(-1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2023时,点A2023的坐标是( ) A、(1009,1011) B、(1009,1010) C、(1010,1012) D、(1010,1011)
A、(1009,1011) B、(1009,1010) C、(1010,1012) D、(1010,1011)二、填空题(本题有6个小题,每小题3分,共18分.)
-
11. 若电影院中的5排2号记为(5,2),则7排3号记为( , ).12. 计算:= .13. 如图,△ABC沿着由点B到点E的方向平移,得到△DEF,若BC=4,EC=1,那么平移的距离是 .
 14. 如图所示,请写出能判定CE∥AB的一个条件 .
14. 如图所示,请写出能判定CE∥AB的一个条件 . 15. 如图,BD平分∠ABC,AD∥BC,∠C+∠DBC=90°,则∠A与∠C的数量关系为 .
15. 如图,BD平分∠ABC,AD∥BC,∠C+∠DBC=90°,则∠A与∠C的数量关系为 . 16. 已知点M(﹣3,3),线段MN=4,且MN∥y轴,则点N的坐标是 .
16. 已知点M(﹣3,3),线段MN=4,且MN∥y轴,则点N的坐标是 .三、解答题(本题有9个小题,共72分,)
-
17. 计算: .18. 如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.求∠C的度数.
 19. 一个正数的平方根是2a-1与-a+2,求a和这个正数.20. 如图,在直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(5,0),C(4,4),
19. 一个正数的平方根是2a-1与-a+2,求a和这个正数.20. 如图,在直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(5,0),C(4,4), (1)、将三角形ABC向上平移2个单位长度,再向右平移3个单位长度,得到三角形A1B1C1 , 请在直角坐标系中画出平移后的三角形A1B1C1 .(2)、求三角形ABC的面积.21. 如图,已知AB∥CD,BC平分∠ABD交AD于点E.
(1)、将三角形ABC向上平移2个单位长度,再向右平移3个单位长度,得到三角形A1B1C1 , 请在直角坐标系中画出平移后的三角形A1B1C1 .(2)、求三角形ABC的面积.21. 如图,已知AB∥CD,BC平分∠ABD交AD于点E. (1)、证明:∠1=∠3;(2)、若AD⊥BD于点D,∠CDA=34°,求∠3的度数.22. 已知点P的坐标为 .(1)、若点P在y轴上,求P点坐标.(2)、若点P到两坐标轴的距离相等,求点P的坐标.23. 如图,四边形ABCD中,点E和点F和分别为边CD和BC上的点,并且∠ABC=∠1,∠A+∠2=180°.
(1)、证明:∠1=∠3;(2)、若AD⊥BD于点D,∠CDA=34°,求∠3的度数.22. 已知点P的坐标为 .(1)、若点P在y轴上,求P点坐标.(2)、若点P到两坐标轴的距离相等,求点P的坐标.23. 如图,四边形ABCD中,点E和点F和分别为边CD和BC上的点,并且∠ABC=∠1,∠A+∠2=180°.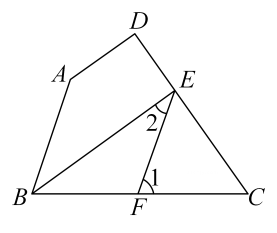 (1)、请判断直线AD和直线BE的位置关系,并证明你的结论;(2)、若BE是∠ABC的角平分线,AD⊥CD,∠FEC=55°,求∠EBF的度数.24. 如图1,已知AB∥CD,∠ACD的平分线交AB交于点E.
(1)、请判断直线AD和直线BE的位置关系,并证明你的结论;(2)、若BE是∠ABC的角平分线,AD⊥CD,∠FEC=55°,求∠EBF的度数.24. 如图1,已知AB∥CD,∠ACD的平分线交AB交于点E. (1)、求证:∠ACE=∠AEC;(2)、如图2,当点F在线段CE上时,连接FA.过点F作FM∥AE交AC于点M,当∠ACD=130°,且∠FAB=25°时,求∠AFC的度数;(3)、如图1,若点F为射线CE上一点.连接FA,探究∠FCD、∠FAB和∠AFC之间的数量关系,并证明你的结论.25. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2m-6,0),B(4,0),C(-1,2),点A、B分别在原点两侧,且A、B两点间的距离等于6个单位长度.
(1)、求证:∠ACE=∠AEC;(2)、如图2,当点F在线段CE上时,连接FA.过点F作FM∥AE交AC于点M,当∠ACD=130°,且∠FAB=25°时,求∠AFC的度数;(3)、如图1,若点F为射线CE上一点.连接FA,探究∠FCD、∠FAB和∠AFC之间的数量关系,并证明你的结论.25. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2m-6,0),B(4,0),C(-1,2),点A、B分别在原点两侧,且A、B两点间的距离等于6个单位长度. (1)、求m的值;(2)、在x轴上是否存在点M,使△COM面积=△ABC面积,若存在,请求出点M的坐标;若不存在,请说明理由.(3)、如图2,把线段AB向上平移2个单位得到线段EF,连接AE,BF,EF交y轴于点G,过点C作CD⊥AB于点D,将长方形GOBF和长方形AECD分别以每秒1个单位长度和每秒2个单位长度的速度向右平移,同时,动点M从点A出发,以每秒1个单位长度的速度沿折线AECDA运动,当长方形GOBF与长方形AECD重叠面积为1时,求此时点M的坐标.
(1)、求m的值;(2)、在x轴上是否存在点M,使△COM面积=△ABC面积,若存在,请求出点M的坐标;若不存在,请说明理由.(3)、如图2,把线段AB向上平移2个单位得到线段EF,连接AE,BF,EF交y轴于点G,过点C作CD⊥AB于点D,将长方形GOBF和长方形AECD分别以每秒1个单位长度和每秒2个单位长度的速度向右平移,同时,动点M从点A出发,以每秒1个单位长度的速度沿折线AECDA运动,当长方形GOBF与长方形AECD重叠面积为1时,求此时点M的坐标.